Excel VBA　数学実験室

　≫ [Amazon書籍] 接続の微分幾何とゲージ理論

　今回は円順列の問題。
　問題が長くて難しそうに思えますが、それほど難しいわけではありません。


[ヒント] こばとちゃんだけが、達郎君と梢ちゃんの間に割り込む可能性があります。
　　
≫ [Amazon書籍] LIBOR マーケット・モデルの実務

解答19（達郎君と梢ちゃんはセットで考えます）

　まず、こばとちゃんを除いた 5 人の並び方を考えます。
　梢ちゃんと達郎君は隣り合っていますから、この 2 人をセットで固定し、


の円順列を考えると並び方は


となります。さらに梢ちゃんから見て達郎君が右隣に座る場合と、左隣に座る場合がありますから、こばとちゃんを除いた 5 人の並び方は、


となりますね。最後にこばとちゃんの席を決めます。

　

　たとえば図のような形で他の 5 人が並んでいた場合、各人の間を □ で表すと、こばとちゃんは 5 つの □ を選べるわけですから、


が答えになります。

[注] 木下達郎君が丹羽梢ちゃんのことを気になっているのは事実ですが、ここまであからさまな我儘を言うことはさすがにありません。問題を作る上での都合ですので、そのあたりはご了承ください。

円順列の基本

　A, B, C, D の 4 人が図のように円卓に座るときの並び方を考えます。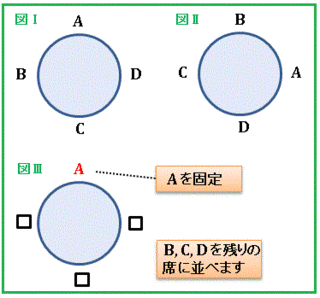

　

　図�Tの並び方は回転させると図�Uに一致しますから、同じ並び方ということになります。そこで図�Vのように A を固定して残りの B, C, D が席に着く並び方を考えればよいので、


となります。一般に、n 個のものを円順に並べる場合の数は


で与えられます。

新人アルバイトの丹羽梢ちゃん

　『こばとの英語ノート』でゴールデンウィーク明けから丹羽梢ちゃんという新キャラを登場させています。大学 4 年生の木下達郎君が就職活動に専念するために 6 月からバイトを１時期休まなくてはならず、人手を確保しておく必要があったからです。そしてこの時期にバイトを採用しておいたことが、今後の展開においても大変助かることになります。今、「真理子さん小学生編」を 3 話に分けて連載していますが、この話自体も次の展開のための伏線のようなものです。この話が終わると一気の急展開が待っています。