問題03 調和平均の性質 [高3★★☆☆☆]
調和平均は次のように定義されます(a > 0, b > 0)。(1) a = 1 とします。 b = 1, 2, 4 について調和平均を求めてください。
(2) a = 1 とします。電卓を使って b = 100, 500 について調和平均を求めてください。
(3) 調和平均の性質を見るために、改めて b = x とおいて、
と表すことにします。 H(x) のグラフの概形を描いてください。
問題を解いてみた人は、調和平均が奇妙な平均だということに気づいたかもしれません。
解答03
(1) ただの計算問題ですが、調和平均のように何だか良くわからない定義に出会ったときには、色々な値を入れて試してみないとその性質は実感できません。a = 1, b = 1 H = 2
a = 1, b = 2 H = 4/3 = 1.333
a = 1, b = 4 H = 8/5 = 1.6
当然のことながら、b の増加と共に平均値も増していきます。
このあたりの感覚は普通の平均と変わりありません。
(2) 極端な値を入れてみると、定義の性質がわかることがあります。
a = 1, b = 100 H = 200/101 = 1.980
a = 1, b = 500 H = 1000/501 = 1.996
このあたりで「おや」と思いませんでしたか?
b = 100 と b = 500 でほとんど値に変化がありません。それ以前に、
「こんなに大きな値を入れたのに、平均値がこんなに小さいの?」
「 1 と 500 の平均値が 1.996 なんて、ありえなくない?」
と思ってしまいますよね。
(3) もう少し解析的に見てみましょう。
H(x) は x > 0 で定義されることに注意してください。
商の微分公式を用いて H(x) の導関数を求めます:
ゆえに H(x) は単調増加関数です。
H(x) の分母・分子を x で割って x ⇒ +∞ の極限をとると H(+∞) = 2a 。
以上より 2a を漸近線とする簡単なグラフが描けます:
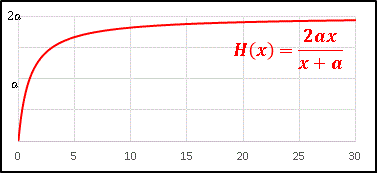
つまり、調和平均 H は b をどれだけ大きくしても決して 2a を超えられなのです。
調和平均の意味
実は調和平均というのは平均時速を得るために用いられます。たとえば、往路・帰路ともに 1km の道のりを往復することを考えます。
往路は徒歩(時速 a = 4 km/h)で、
帰路は超伝導リニア(時速 b = 500 km/h)に乗ります!
「たった 1km をリニアで? 馬鹿な設定だなー」
とか思わないでくださいな。あくまで解説を分かりやすくするためですから。
さて往路・帰路で要する時間は、それぞれ
Ta = 1/a = 1 [km] /4 [km/h] = 1/4 [h]
Tb = 1/b = 1 [km] /500 [km/h] = 1/500 [h]
帰路はほとんど一瞬(7.2 秒)です!
すごいですねー。リニアの開通が待ち遠しいですね。
では徒歩とリニアの平均時速を求めてみましょう。
道のりは往復合わせて 2km ですよ。
H = 2/(1/4 + 1/500) = 7.93 km/h
リニアを使ったのに平均時速はたった 8 km/h となります。
「そんな馬鹿な!」と思いたくなりますが、調和平均の定義を使うとこうなってしまいます。こうなってしまった原因は往路に相当な時間がかかってしまっていることにあります。1/4 時間という大きな値 a が分母にあれば、リニアでいくら b を小さくしたところで、おのずと値に限界が生じてしまうわけです。別の言い方をすると「徒歩でかかってしまった時間は決して取り戻すことができないので、平均時速を大幅に下げてしまう」ということです。
『九石絵里子の日記帳』もよろしくです
4 月から始めている架空日記小説『九石絵里子の日記帳』も快調に記事を積み重ねています ...... が、グーグルの検索エンジンからの入りがとても少ないです。やはりこの妙なタイトルでは検索ワードにかからないかもしれませんね。にもかかわらず、開始当初にブログランキングで 100 を超える OUT ポイントがあって調子に乗って浮かれていましたが、1週間ほど経つとポイントが続落 ...... その理由は作品の質にあるのだと自省しております。キャラを増やし過ぎて焦点がぼやけましたし、ストーリーもシンプルなコメディ路線から外れてしまっていました。ここは素直に反省して、もう1度原点に立ち返ろうと思っています。いくつか「あはは」と笑えそうな記事を下にピックアップしておきましたので、ぜひまたお寄りください。⇒ タフガイ兄さん、急病ですか!?