���04�@�O�p�����܂������̔��� [���R����������]
�@(1) cosx + sinx = 0 ���݂����ŏ��̐��� �� �����߂Ă��������B�@(2) 0 �� x < �� �͈̔͂� f(x) �����̂悤�ɒ�`���܂��F
�@�@y = f(x) �̃O���t�̊T�`��`���Ă��������B
�@
��04�i���̔��������͎g��Ȃ��ق��������ł��j
(1) �O�p���̊�b���ł��B�@�@cosx �� sinx �����������Ŏ���ό`���܂��F
�@���ɂ́u�ŏ��̐����v�Ə�����Ă��܂�����A
�@�������ƂȂ�܂��B
(2) 0 �� x < 3pi/4 �͈̔͂ōl���܂��B
�@f(x) �̔����ɂ͏��̔���������p���Ă��悢�̂ł����A���������Ⴒ����ƌ��ɂ����Ȃ��Ă��܂��ĊԈႢ�₷���ł��B�����������ʂ���ǂ����邽�߂ɁAf(x) �̕���E���q�� cosxsinx �Ŋ����Ă݂܂��B
�@������ u = 1/sinx, v = 1/cosx �ƕϐ��ϊ�����ƁA
�ƂȂ�܂�����A���Ƃ͍������̔���������p���āA
�������܂��B�ɒl���Ƃ� x �����߂�ɂ� f'(x) = 0 �Ƃ����āA
u' + v' = 0�@�@�@(*)
�Ƃ����������������Ηǂ����Ƃ��킩��܂��B
�ł�����A����� (*) �ɑ�����Đ�������ƁA
cos3x - sin3x = 0
�������܂��B���ӂ������������āA
�@�@�@�@�@�@�@�@(cosx - sinx)(cos2x + cosxsinx + sin2x) = 0
�@�@�@�@�@�@�@�@(cosx - sinx)(1 + cosx siny) = 0
���������āA
�@�@�@�@�@�@�@�@cosx = sinx�@�@�@(a)
�@�@�@�@�@�@�@�@sin2x = �|2�@�@�@(b)
�̂Q�̕������������܂����A
(b) �����������Ȃ����Ƃ͖��炩�ł��i�|1 �� sin2x < 1�j�B ����� (a) ����
�������A���̂Ƃ� f(x) �͋ɒl
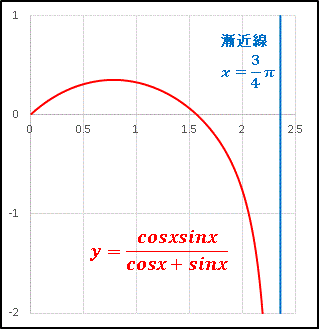
���Ƃ�܂��B x �� �� = 3pi/4 �̋Ɍ����l����ƁA����� 0 �ɋ߂Â��A���q�̕����͕��ɂȂ�܂��icosx < 0, sinx > 0�j����A�|�� �ɔ��U���邱�Ƃ��킩��܂��B����� f(0) = 0 �ł��B�ȏ���O���t�̊T�`�͉��}�̂悤�ɂȂ�܂��B
�@
���n�p�P��C�@�ʓx�@
�@circular method�@�ʓx�@
�@circle�@�~
�@radius�@���a
�@circular constant�@�~����
�@central angle�@���S�p
�@sector�@��`
�@arc�@��
�@radian�@�ʓx
�@circle�@�~
�@radius�@���a
�@circular constant�@�~����
�@central angle�@���S�p
�@sector�@��`
�@arc�@��
�@radian�@�ʓx
�@sector �� ����ꂽ�isect�j���̂Ƃ����j���A���X���܂މp�P��ŁA�u����A����A���A���n��v�Ȃǂ̈Ӗ��ŗp�����܂��B
�@ �@