必ず極小値が存在します
前回記事で「 x → ∞ のとき logx/x → 0 」を証明するときに、y = √x - log(x)
という関数が登場しました。今回はこれをもう少し一般化して
y = xa - blog(x) (x > 0) [1]
という関数を扱ってみます。 x > 0 ですから a は任意の実数をとることができますが、関心があるのは 0 < a < 0.5 の辺りのふるまいです。まずは b = 1 に固定して a = 0.5, 0.4, 0.3 というように変化させてみます:
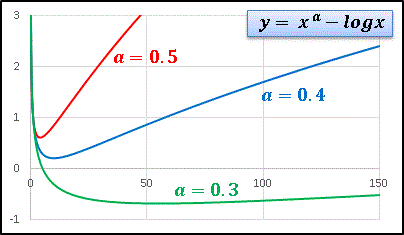
この関数が a の僅かな変化に対して非常に敏感に応答することがわかります。⊿a = 0.1 の小さな刻み幅であってもグラフ全体がどんどん下に落とされていきますね。次は a = 0.5 に固定して b の値を変化させます:
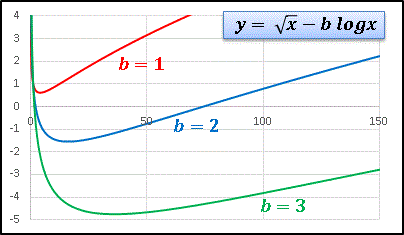
先程のように sensitive ではありませんが、b が増加するとやはりグラフは下へ落ちます。
さてここで、もう1度前回に証明した公式
を思い出してください。logx に係数 b をかけてもやはり 0 に収束します。
a がどれほど小さくなろうと、或いは b をどれほど大きくしようと、十分に大きな x においては xa が blogx に優ります。したがって必ずどこかで増加へ転じます。つまりこの関数には必ず極小値が存在します。それでは極値をとる x はどのような方程式を満たすのか調べてみましょう。 [1] を微分すると
y´= axa-1 - b/x
ですから、y´= 0 とおくと
x = (b/a)1/a
が得られます。極小値は a, b についての 2 変数関数として
MIN(a, b) = (b/a)[1-log(b/a)]
と表されます。つまり極小値は a と b の比率 k = b/a の関数になっていますね。
改めて k の関数として書き直しておきましょう:
MIN(k) = k [1 - logk] [2]
たとえば、a = 0.5, b = 1 であれば k = 2 ですから、
MIN(2) = 2[1-log2] = 0.614
と計算できます。
才能について
人にはやはり持って生まれた才能というものがあって、ある分野で頂点に近づくほど、努力ではなかなか越えられない壁というものがあると思うのです。特にスポーツの世界では毎日のように厳しい競争にさらされますから、そういう面がより顕著なのではないでしょうか。やはり子供の頃から抜きんでた反射神経とか、頑丈な身体というもを備えていないと、一流のアスリートになることは難しいと思います。よくインタビューなどで「いやあ。僕には才能なんてものはないんですよ。努力でここまできたんです」とおっしゃる方もいますが、それはおそらくプロになれるかなれないかの、ぎりぎりの線にいるような(高校選手権のベスト4以内とか)狭い母集団の中で比較した話であって、世間一般の人と比較したものではないはずです。近頃では遺伝子検査によって「君は短距離走に向いている」とアドバイスされて進路を決める子供たちもいるようです。学問や芸術、文学などの世界では評価基準が複雑ですから、後天的な要素の割合が増すと思いますが、それでも遺伝的な要因を抜きにして考えられないと思います。
そういう特別な才能をもった人たちを正直羨ましいと思いますが、ふとこんなことを思いました。たとえば "筋肉質な身体" というようなものまで才能に含めるとすれば、見た目は平凡でも "病気になりにくい" とか "長寿である", "ストレスに強い" という遺伝子を持っていることも1つの才能なのではないでしょうか。こういう人たちは、普段は特に注目されることはないままに日常生活の中で地味に才能を発揮していることになります。