立ち上がりに特徴がある関数です
今回はあまり見慣れない関数を扱ってみます:y = xa/x [1]
式を眺めているだけでは、どうにも概形を想像しにくいですね。
早速グラフを描いてみます;

原点付近で急速に立ち上がって最大値に達したあとに値を落としていきますが、 a の値の増加にともなって、頂点から x 軸正方向への勾配も急激になります。実はこの関数、立ち上がりにも特徴があります。原点付近の拡大図を見ると、 a の値が大きいほど立ち上がりは遅くなっていることがわかります。これは x < 1 ではその指数が大きいほど値が小さくなることに対応しています。
さて、図を見ると「 a の値によらず 1 に収束するのではないか?」という予想が立ちますね。証明してみましょう。 [1] のままでは扱いにくいので両辺の対数をとってみます:
logy = a(logx/x)
ここで x → ∞ で logx/x → 0 [*] が知られていますから、
logy → 0 ⇔ y → 1 (x → ∞)
となって [1] は 1 に収束します。(証明終わり))
x → ∞ で logx/x → 0 の証明
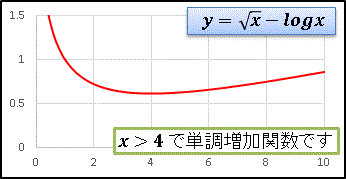
曖昧なまま [*] を使うことをためらわれる人もいるかもしれませんので、「はさみ打ちの原理」を使って証明してみましょう。そのために、f(x) = √x - log(x)
という関数を考えてみます。上式を微分すると、
f´(x) = (√x - 2)/(2x)
が得られます。x > 4 で f´(x) > 0 (単調増加)がいえますね。
また、 e/2 > 1 なので(e = 2.718 ですよ。念のため)
f(4) = 2log(e/2) > 0
も成り立ちます。したがって
0 < logx < √x (x > 4)
が成り立ちます。x で割って
0 < logx/x < 1/√x (x > 4)
だから x → ∞ の極限をとると「はさみ打ちの原理」により
logx/x → 0 (x → ∞)
が成立します(証明終わり)。
しかし極限値1つ求めるために、いちいち「はさみ打ちの原理」なんて使っていては面倒です。実はもっと簡単な方法があります。それは「ド・ロピタルの法則」を用いる方法です:
「ド・ロピタルの法則」は 0/0 や ∞/∞ のような不定形に対して威力を発揮する極限の計算法です。「平均値の定理」と「コーシーの平均値の定理」を経て証明できますので、気になる人は解析学の本で確認してください。この法則を使えばより一般的な logx/xn についても1発で極限値を求めることができます:
この式は対数関数の性質を表すとても重要な定理です。
どんな小さな正数 n においても、logx は xn よりもゆっくりと増加する
ということを示しています。 n は正の数であれば何でもよいのです。たとえば「 x が十分大きいところでは、 logx は x0.01 よりも緩やかな勾配をもつ」のです。驚きですね!
がむしゃらに勉強するだけでは ......
若くてエネルギーに満ちている時ほど、全力投球で数学の本と格闘しようと意気込みがちです。真面目な人ほど「よし。証明が理解できたぞ! 次の章に進もう」とか「演習問題をがんがん解いて力をつけるぞ!」というような "がむしゃら勉強法" になってしまうことがあります。でもやっぱりちょっと肩の力を抜いてみることも大切だと私は思うのです。少し引いたところから、目の前に書かれていることを眺めてみる余裕をもつと、途中で息切れすることもなくなります。何か新しい定理や公式に出会ったときは、証明法や公式の使い方にばかり目をとられずに、お茶でも淹れてゆったりと頭をリラックスさせながら。「この定理がいったいどういうことを意味しているのか」、「何のためにこの公式が存在するのか」ということに思いをめぐらせてみてください。そのためには、本に載せられた演習を解くだけではなく、「この結果はつまるところ何を意味しているのだろう」と思うことが大切です。今回の記事では「 x → ∞ のとき logx/x → 0 」を2つの方法で証明しましたね。でもそれだけで終わってしまうと、単に「極限値を問う演習問題を1つ解いた」というだけのことで終わってしまいます。苦労したわりには、さほどの収穫がありません。むしろこの1歩先のことが大切で、「これはつまり logx と xn の関係は ...... 」と思考を進めてみると、対数関数についての理解が深まります。そうすると「今日も収穫があったなあ。数学は楽しいなあ」という充足感が得られ、継続する動機にもなります。数学は ...... いえ数学に限らず学問とお付き合いするときは、焦らずにゆっくりと Step by step です!