ROUNDDOWN(数値, 残す桁)
という形で引数を指定します。81.54593 という数字に適用すると、
ROUNDDOWN(81.54593,-1) = 80
ROUNDDOWN(81.54593,0) = 81
ROUNDDOWN(81.54593,1) = 81.5
ROUNDDOWN(81.54593,2) = 81.54
ROUNDDOWN(81.54593,3) = 81.545
このような値を得ることになります。
2つ目の引数指定は "残す桁" と覚えておくとわかりやすいです:

y = rounddown(x, 0) のグラフに描くと次のようになります:
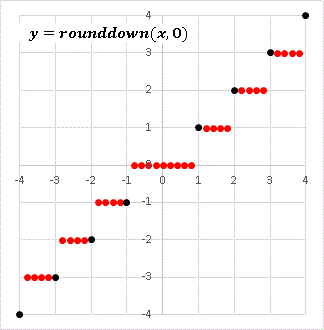
飛び値のところは黒丸で表示しています。
y = rounddown(xsinx, 0) としてみると・・・・・・

こういう面白いグラフが描けます。