[Ctrl] + [Z] 直前の操作を元に戻します。
[Ctrl] + [Y] 直前の操作を繰り返します。
INT関数で実数から整数部分を得ます
INT関数 は数学のガウス記号 [x] ( x を超えない整数値)に相当する演算です。INT は integer(整数)の略号です。 INT() は引数に全ての実数を指定できます。
INT(正数) は小数部分を切り捨てます。
INT(2.6) = 2
INT(13.3) = 13
INT(負数)は小数部分を切り捨てて、0 から離れたほうの整数値に丸めます。
INT(−7.5) = −8
INT(−0.3) = −1
なぜこのような演算定義になっているのかを、
y = int(x)
という関数のグラフを描いて説明します。

−4 ≦ x ≦ 4 の範囲で刻み幅 0.2 で描いています(実際には各ドットの集まる部分は線分になります)。x = −3, −2, −1, 0, 1, 2, 3 という整数部分で「飛び跳ねる」関数になっていますね。飛び跳ねの位置は黒丸で示してありますが、負の領域から正の領域まで一定の周期で飛び跳ねていることがわかります。もし一般的な端数切り捨て演算である ROUNDDOWN という関数で処理すると、グラフは次のようになってしまいます。
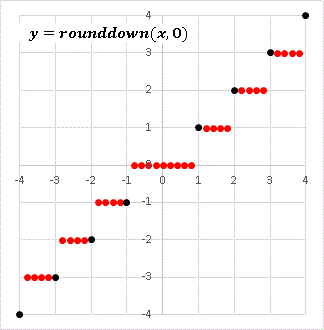
原点付近で周期が崩れていますね。したがって、数の性質を扱う「数論」などの分野では、切り捨て演算として [x] の定義を用いているのです。
INT 関数 応用編
x の刻み幅を細かくして、次のような関数を考えてみます:
y = [int(x)] 2
各 x の整数値を取得して 2 乗するという関数です。グラフを描いてみると・・・・・・
![y=[int(x)]^2.gif](/excelmathfunction/file/y3D5Bint28x295D5E2.gif)
int(x) が整数なので、平方した y もまた 1, 3, 9, 16, ・・・・・・というような整数値のみをとります。
今度は int(x) を指数関数に入れてみましょう:
y = exp[int(x)]
という関数を作ってグラフを描いてみると・・・・・・
![y=exp[int(x)].gif](/excelmathfunction/file/y3Dexp5Bint28x295D.gif)
飛び飛びの指数関数が得られます。