[↑][↓][←][→] 選択セルを移動します
空気抵抗を受けるバネの振動を表す曲線
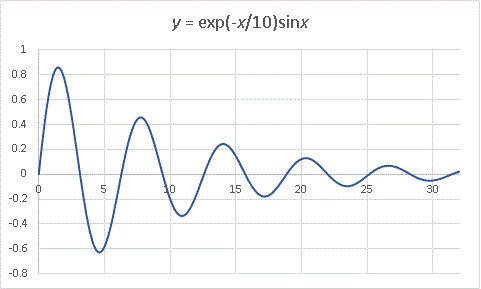
これは物理学でよく見かける形です。空気抵抗を受けるバネの振動です。exp(-x) をそのまま乗じてしまうと、減衰が効きすぎてしまうので変数を1/10に抑えておきます。
これを眺めていても別に面白くないので、以前(第6回)に出てきた y = sin(x 2) にexp(-x/10) を乗じてみますと・・・・・・
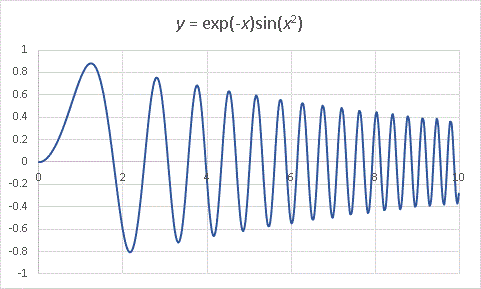
減衰しながら周期もどんどん短くなるというグラフが完成しました。
次は sinx に x を乗じた関数のグラフを描いてみます:
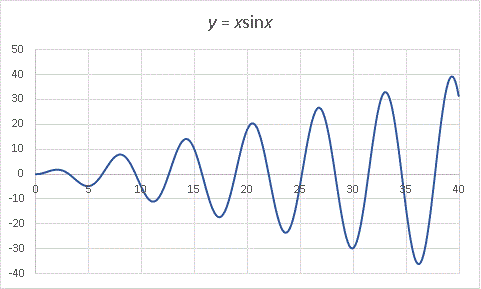
これは理数系なら誰でも一度は見たことのあるグラフ。わざわざ描かなくても振幅が徐々に増していく三角関数だということは予測できます。この振幅増加を抑え込むために exp(-x/10)を乗じると・・・・・・

一度振幅を増加させて、そのあと減衰させてゆくという関数ができあがります。指数関数の減衰効果のほうが一次関数の増大効果より大きいのです。
⇒ なんとなくの数学日記始めました