分かりやすい高校数学:確率(8)組み合わせ
前回 ⇒ 確率(7)順列
８回目ですー．今日もサクサクいくよー．サクッと．
今回はついに，高校数学Ａの確率で最重要（と個人的に思っている）「組み合わせ」です！ これができれば，順列・組み合わせの両方をマスターできることになるわけですね．でも実は，もう組み合わせを簡単に理解できるようになっているはずなんですよ．いままでの話だけでね．なので，サクッと進めてみます！
組み合わせの典型的な問題文は，「５個のボールから２個選ぶ方法は，何通りあるか？」です．順列の時と似ていますが，「選びだしたボールを並べる方法」については聞いていない点が違います．そう，つまり「ボールは選びだすけど，並び方は気にしないで」ということです．あれ，どこかで聞いたフレーズですね．
そう，順列の時に，余ったボールに対してつけられていた条件と同じですね．さぁ，ここで今一度思い出しましょう．
全体の並べ方から，一部の並べ方を無視したいなら．．．
全体の並べ方を，無視したい部分の並べ方で割るんだぁ！！！
そう，ここでは「選んだボールの並べ方」を無視したいのだから，選び出したボールの個数の並べ方である2の階乗で割ればいいのです！！！さて，この考え方を適用すると図のようになります．
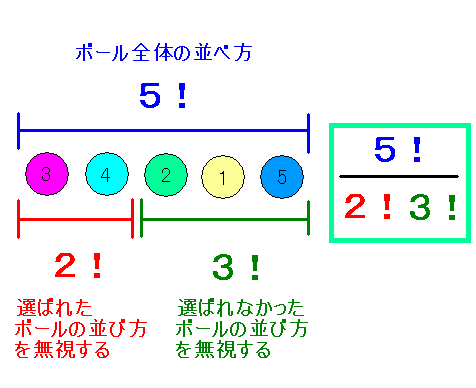
さぁ，この問題の答えは
5! (ボール全体の並べ方）÷3! (余ったボールの並べ方) ÷2! (選んだボールの並べ方)
となります！！重要なことは，余ったボールの並べ方も気にしないことに加えて，選んだボールの並べ方も気にしないという点です．だから，3! と 2! の二つで割るんですね．
次に，順列の時と同じように数式で考えてみましょう．n個のボールの中から，r 個のボールを選びだす方法について考えます．この時の組み合わせ方法は，nCr と表現されます．
順列の時と違うのは，選びだしたボールの並びを無視するために，r ! で割っている点だけです．順列も組み合わせも，考え方は似ているんですね．
さて，さらに組み合わせの応用問題を解いてみましょう．
問題「9個の石を，4個，3個，2個に分ける方法は何通りあるでしょうか？」
今回は選びだすというものでなく，グループ分けです．しかも三つのグループです．でも，基本的に組み合わせの考え方と変わりません．選びだすということは，選ぶものと選ばないものにグループ分けするのとほぼ同じです．そして，グループ数が三つであっても，無視したい部分の並べ方で割るという考え方は変わりません．
よって，9! ÷ 4! ÷ 3! ÷ 2! となります．実際，なんら難しいことはありませんね．
さーサクッと次の問題いってみましょうか！
問題「9個のボールを，3個, 2個, 2個, 2個に分ける方法は何通りか？」
これも簡単！ 9! ÷ 3! ÷ 2! ÷ 2! ÷ 2! ですね，，，，，というのは間違いです！！！！！！さて，なぜでしょうか？
この問題となるのは，「2個のグループが複数ある」ことです．そう，組み合わせを考えた時，このグループの間で重複が生まれてしまうからなんですね．
前回の問題は，４個，３個，２個の組み合わせに分けていたので，重複は生まれませんでした．含まれている数量が違うので，４個のグループを３個のグループと入れ替えることはできないからです．しかし，今回は２個のグループが複数あり，それらを入れ替えることができるために，重複が生まれてきます．
では，これを対処するにはどうしたらいいのか？ここでもあの言葉を思い出してください！！！
全体の並べ方から，一部の並べ方を無視したいなら．．．
全体の並べ方を，無視したい部分の並べ方で割るんじゃぁ！！！
今無視したいのは，２個のグループの並べ方ですね．ここの並べ方を無視してあげれば，重複はなくなります！今，２個のグループは３つあるわけですから，その並び方は3! です！！よって，この問題の答えは，9! ÷ 3! ÷ 2! ÷ 2! ÷ 2! ÷ 3! となります．
今回までの組み合わせの問題では，それぞれ異なる数字の書かれたボールを扱いました．これは，それぞれの区別がつくということを意味します．それでは区別つかない場合はどうなるのでしょうか．たとえば，10円玉3枚と5円玉2枚の並べ方は？という問題などです．実はこの問題も，あの考え方を使って解くことができます．
その話はまた次回！！！
次 確率(8)区別なしの順列
８回目ですー．今日もサクサクいくよー．サクッと．
今回はついに，高校数学Ａの確率で最重要（と個人的に思っている）「組み合わせ」です！ これができれば，順列・組み合わせの両方をマスターできることになるわけですね．でも実は，もう組み合わせを簡単に理解できるようになっているはずなんですよ．いままでの話だけでね．なので，サクッと進めてみます！
組み合わせの典型的な問題文は，「５個のボールから２個選ぶ方法は，何通りあるか？」です．順列の時と似ていますが，「選びだしたボールを並べる方法」については聞いていない点が違います．そう，つまり「ボールは選びだすけど，並び方は気にしないで」ということです．あれ，どこかで聞いたフレーズですね．
そう，順列の時に，余ったボールに対してつけられていた条件と同じですね．さぁ，ここで今一度思い出しましょう．
全体の並べ方から，一部の並べ方を無視したいなら．．．
全体の並べ方を，無視したい部分の並べ方で割るんだぁ！！！
そう，ここでは「選んだボールの並べ方」を無視したいのだから，選び出したボールの個数の並べ方である2の階乗で割ればいいのです！！！さて，この考え方を適用すると図のようになります．
さぁ，この問題の答えは
5! (ボール全体の並べ方）÷3! (余ったボールの並べ方) ÷2! (選んだボールの並べ方)
となります！！重要なことは，余ったボールの並べ方も気にしないことに加えて，選んだボールの並べ方も気にしないという点です．だから，3! と 2! の二つで割るんですね．
次に，順列の時と同じように数式で考えてみましょう．n個のボールの中から，r 個のボールを選びだす方法について考えます．この時の組み合わせ方法は，nCr と表現されます．
順列の時と違うのは，選びだしたボールの並びを無視するために，r ! で割っている点だけです．順列も組み合わせも，考え方は似ているんですね．
| ◆ 付け足しメモ ◆ ちなみに，nCn-r = nCr となります．これはどちらも，５個( n )のボールを２個( r )と３個( n-r )に分ける点で同じだからです．分けた後で，最終的にどちらを使うかという違いしかないからですね．計算式も同じになっていることからも分かるかと思います． |
さて，さらに組み合わせの応用問題を解いてみましょう．
問題「9個の石を，4個，3個，2個に分ける方法は何通りあるでしょうか？」
今回は選びだすというものでなく，グループ分けです．しかも三つのグループです．でも，基本的に組み合わせの考え方と変わりません．選びだすということは，選ぶものと選ばないものにグループ分けするのとほぼ同じです．そして，グループ数が三つであっても，無視したい部分の並べ方で割るという考え方は変わりません．
| ◆ 付け足しメモ ◆ ここで，「ほぼ」と言っているのは，実際は少し違う場合があるからです．その違いはのちほど触れていきます． |
よって，9! ÷ 4! ÷ 3! ÷ 2! となります．実際，なんら難しいことはありませんね．
さーサクッと次の問題いってみましょうか！
問題「9個のボールを，3個, 2個, 2個, 2個に分ける方法は何通りか？」
これも簡単！ 9! ÷ 3! ÷ 2! ÷ 2! ÷ 2! ですね，，，，，というのは間違いです！！！！！！さて，なぜでしょうか？
この問題となるのは，「2個のグループが複数ある」ことです．そう，組み合わせを考えた時，このグループの間で重複が生まれてしまうからなんですね．
前回の問題は，４個，３個，２個の組み合わせに分けていたので，重複は生まれませんでした．含まれている数量が違うので，４個のグループを３個のグループと入れ替えることはできないからです．しかし，今回は２個のグループが複数あり，それらを入れ替えることができるために，重複が生まれてきます．
では，これを対処するにはどうしたらいいのか？ここでもあの言葉を思い出してください！！！
全体の並べ方から，一部の並べ方を無視したいなら．．．
全体の並べ方を，無視したい部分の並べ方で割るんじゃぁ！！！
今無視したいのは，２個のグループの並べ方ですね．ここの並べ方を無視してあげれば，重複はなくなります！今，２個のグループは３つあるわけですから，その並び方は3! です！！よって，この問題の答えは，9! ÷ 3! ÷ 2! ÷ 2! ÷ 2! ÷ 3! となります．
| ◆ 重要ポイント ◆ 問題文が「9個のボールから7個選んで，3個, 2個, 2個に分ける方法は何通りあるでしょうか？」であった場合の答えは，9! ÷ 3! ÷ 2! ÷ 2! ÷ 2! ÷ 2! になります．9個のボールを3個, 2個, 2個, 2個にグループ分けするという点では変わらないのですが，三種類ある２個のグループのうちの一つは，選ばれないグループであり，選ばれる他二つのグループと入れ替えることができないため，並べ方に含めて考える必要はないわけです．選ばれないグループはある意味，捨てられているわけですから，選ばれているグループと交換できないわけですね．よって，含める必要のある，二つのグループに対しての並べ方である，2! で割ることになります． これが先ほど言った，「グループ分けする」のと，「選ぶ選ばないの二つに分ける」ことの違いです．「グループ分け」ではそれぞれのグループの違いはないですが，「選ぶ選ばない」では違いが現れます．よって，「４つのボールから二つ選ぶ」場合は，4! ÷ 2! ÷ 2! = 4C2になりますが，「４つのボールを二つずつに分ける」場合は，4! ÷ 2! ÷ 2! ÷ 2!になります． |
今回までの組み合わせの問題では，それぞれ異なる数字の書かれたボールを扱いました．これは，それぞれの区別がつくということを意味します．それでは区別つかない場合はどうなるのでしょうか．たとえば，10円玉3枚と5円玉2枚の並べ方は？という問題などです．実はこの問題も，あの考え方を使って解くことができます．
その話はまた次回！！！
最近は大人が数学を勉強し直すことがブームになっているようです．．あのころできなかったことに，再チャレンジしたいという人が多いみたいですね．そんなブームに一役買っているのがこの「数学ガール」です．
前回の順列の際にも紹介しましたけど，こちらは漫画版です．数学を題材として数学に慣れ親しめるようにする上では，漫画は良い方法ではないかなーと．もちろん，きちっと理解をしたいのであれば，原作である小説版を読んだ方がいいと思うのですが，入口としてはできるだけ簡単な方がいいのは事実ですよね．数学に慣れ親しむってのは，このサイトのコンセプトでもありますしね． |
次 確率(8)区別なしの順列
【確率の最新記事】
確率１
この記事へのコメント