Excel でおにぎりとカレーパン?
たとえば次のようなグラフです。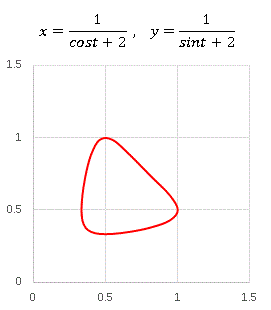
媒介変数 t が動くと (x,y) は おにぎり のような形の曲線上をぐるぐる回り続けるわけです。何故おにぎりに例えるのかというと、他に思いつかなかったからです。さて、この関数を少し変形すると ......
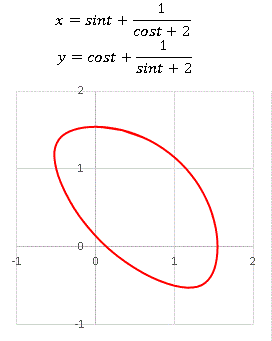
カレーパン のような形の曲線上をくるくる動くことになります。何故カレーパンに例えるのかというと、私の好物だからです。特に揚げたてのカレーパンの美味しさときたら「高級フランス料理だって太刀打ちできないぞ」と思ったりしています。引き続いて次のような曲線。
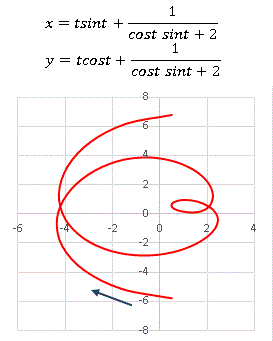
−2π < t < 2π の範囲で描いています( pi は円周率)。動点 (x, y) は下の方から青い矢印の方向へ移動します。今回は sint や cost に媒介変数 t が乗じられているので閉曲線にはならず、t の増加と共に原点に近づいていき、そのあと遠ざかっていきます。もう少し t の範囲を広げてみましょう。
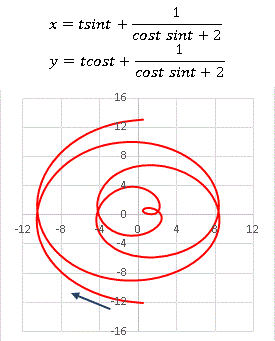
範囲は−4π < t < 4π です。矢印に沿って曲線を丁寧に目で追っていけば、軌道が螺旋を描いていることがわかると思います。
ところで動点が最も原点に近づくときの座標はどこでしょうか? 微積分の手法を用いて原点からの距離が最小となる点と、その最小値を求めることも不可能ではないかもしれませんが、式が複雑すぎてたいていの人は途中で嫌になると思います。私は面倒なので計算する気にもなりません。エクセルを使ってラクをしましょう。原点最近接点を与える媒介変数 t と動点座標 (x, y) 、および距離 r は、
t = −0.1396rad (8deg)
(x,y) = (0.5564, 0.3987)
r = 0.6842
(x,y) = (0.5564, 0.3987)
r = 0.6842
となります。もし「手計算で求めたよ!」という強者がおられたら、コメントしてください。
⇒ なんとなくの数学日記(エクセルと数学)