新規記事の投稿を行うことで、非表示にすることが可能です。
2023年05月19日
08035 大人のさび落とし 図形と方程式 領域内の最大値・最小値(2)
大人のさび落とし
図形と方程式 領域内の最大値・最小値
(2)
001
三つの不等式に
囲まれた 領域D
があるんですが
その 領域を 図示し
領域内を 点が動くとき
x二乗 +y二乗の
最大値 最小値を もとめなさい
という問題
002
三本の 不等式をですジャン
直線に 見て
交点を A,B,C 求めると
003
➀②から 行ってみますと
引算すれば
x が 消去できて
yの 式になるので
y=0
②に y=0を 代入して
x=6
004
普段見慣れた
直線の式に書き換えれば
➀②の 交点Aは
A(6,0)
005
②③の 交点は
今度は
③から ②×2を 引き算すれば
xが 消去できて
yの式になるから
y=21/5
006
y=21/5を ②に代入して
x=9/5
これを 点C(9/5,21/5)
007
見慣れた かたちにすれば
こんな感じで
交点Cは ここ
008
③➀の交点は
➀と③を 足せば
yが消去できるので
x=ー1
x=ー1を ➀に代入して
y=7/3
これを点B ( -1,7/3)
009
見慣れた 形にして
交点は ここ
010
以上まとめて
不等式の 示す領域は
三角形の 3辺上を含む 内部
これが 集合D
011
x、yが D内を 動くとき
x二乗 +y二乗の
最大値 最小値は
先ず 最小値から
x二乗 +y二乗=K とすれば
これは 原点中心の 半径√Kの円
円が 辺ABに 接するときが
最小値になるから
012
辺ABの式を
円の式に 代入して
接する条件で
判別式D D=0
とすれば
013
こんなでしたね
014
kは 18/5
これは そのまま
x二乗 +y二乗の 最小値
別解もあってですね
点と 直線との 距離
公式に 入れれば
6/√10
015
x2 +y2=k とした時
kは 半径の 二乗
k=(√k)2
点と直線との距離は
半径で出てくるので
kを求めるには
2乗して いただいて
18/5
016
最大値は
半径を
伸ばしてきますと
点Aを 通過するときが 最大値
017
領域と 2x+y
2x+yが
領域内で
最大・最小になるときは?
018
2x+y=kと置いて
式変形して行くと
y=-2x+kで
この 傾きの直線の
y切片の 変化だとわかるので
019
円と直線でできた
領域の
第一象限での 交点は
020
(x,y)=(1,2)の時
その交点を
通過するときが
最大なので
最大値4
021
最小値は
y=ー2x+kが
円と接するときで
第三象限で
接するとき
022
直線を 円に代入して
判別式で
接するときを
求めると
023
最小値は-5
024
こんな感じカナ
025
問題
この不等式の
領域内に
式が 入ってるように
026
この式はさ
=k と置いて
変形してくと
半径は変わるんだけど
円の方て式になってるので
027
領域の 境界線との関係で
接する 交わる を 調べると
代入して
判別式
028
この 判別式が
ゼロ 以上ならいいのだから
029
こんな感じになるですね
030
図にすると こんなイメージで
031
x、yが これこれの
不等式を 満たすとき
x+yの 最大値が
=2になる様に
負の定数Pを 求めなさい
032
二次関数の グラフで
領域が できてるので
標準形にして
頂点を みると
033
で
Pは 負の定数であるから
034
分かってる 条件で
図を 書いてみると
この 2次関数が
直線 y=ーx+2に 接する 様に
035
であるがため
②を ➀に 代入して
判別式D D=0を見ると
036
因数分解で来て
037
Pは -3
038
代入して
判別式を みれば 接してるでしょ
お疲れ様です。
2023年04月21日
08034 大人のさび落とし 図形と方程式 領域での最大・最小
大人のさび落とし
図形と方程式 領域での最大・最小
01
領域を 表す式が与えられていて
その領域内を
点(x、y)が 動くとき
y+2xの 最大 ・ 最小を
求めてちょうだい。

02
まず 領域を 見える様に
絶対値が 苦手な方も
けっこう いらっしゃいますが
慣れだからさ
絶対値が ついてるがために
答は 正なんですが
絶対値が付いてないと
中味がじゃナイスカ
負の時と 正の時があるですので

03
少し整理して
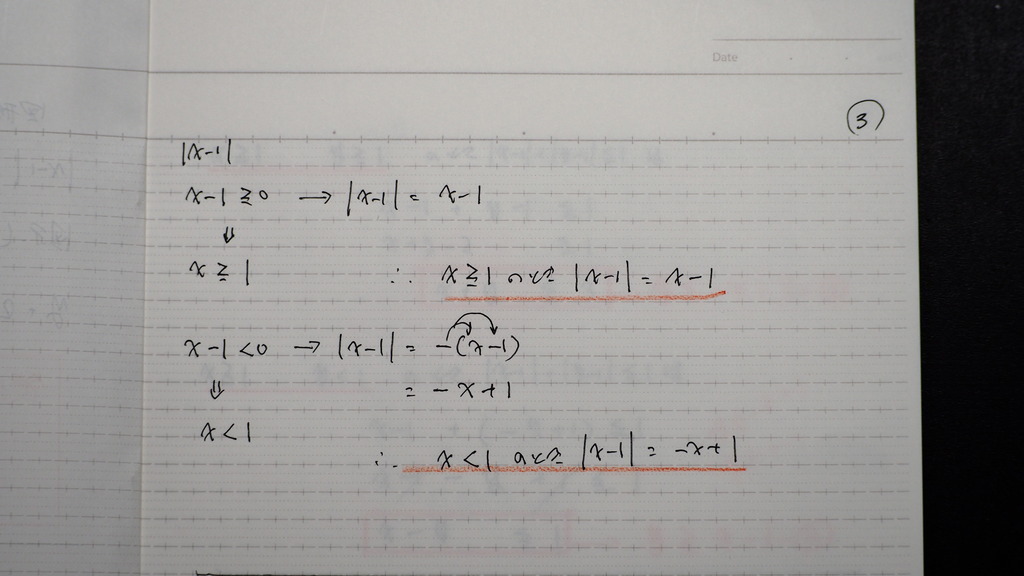
04
こんな感じに
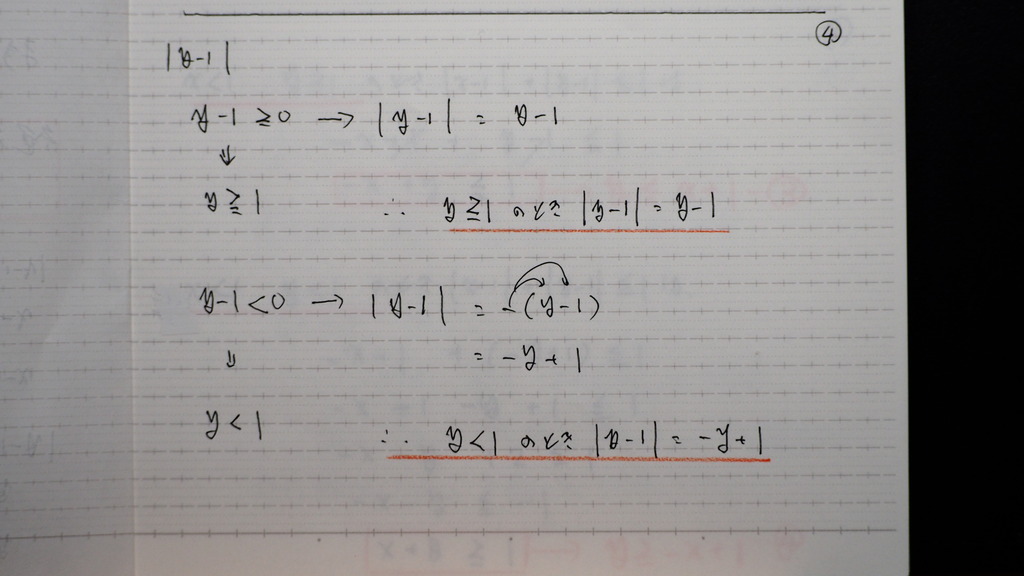
05
さらに 少し整理して
傾きと y切片が わかる形にして

06
わたしんとこは
子供は
学校も出ずに
毛皮を着て
猫っていうんですが
9匹のメス
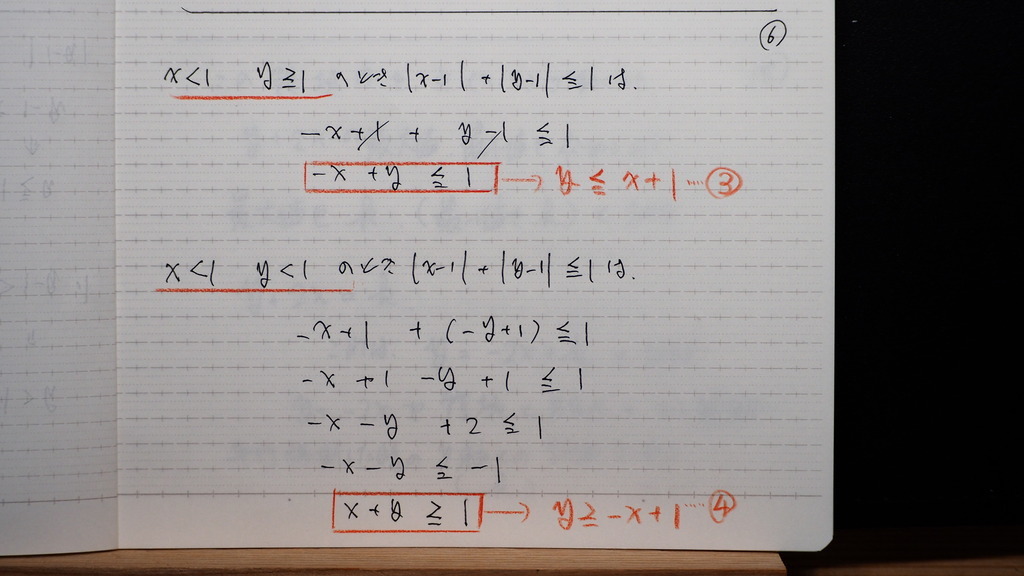
07
話を 元に戻して
こんな感じに
整理できました
これが
与式の 表す領域ですよ
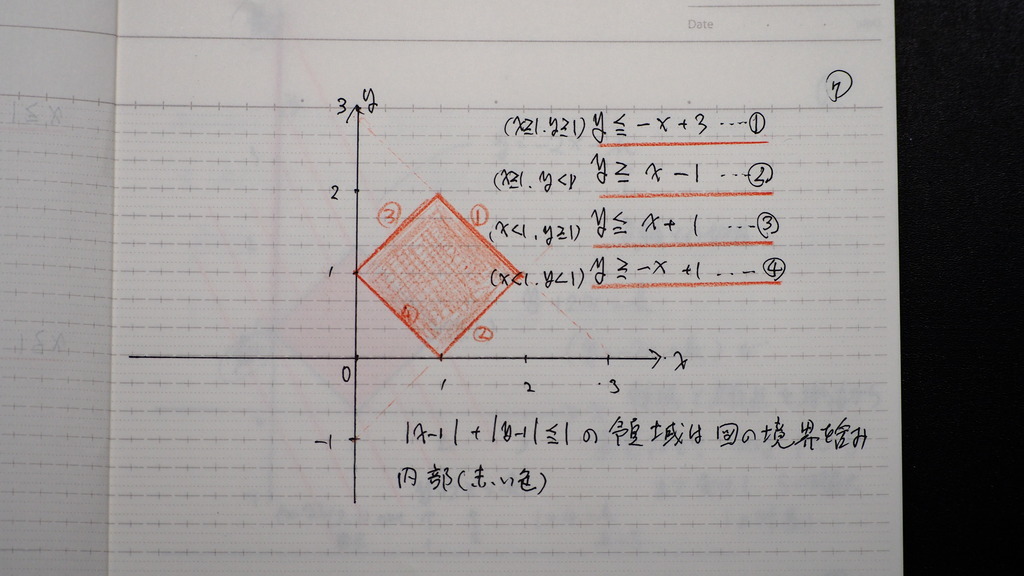
08
ここから
y+2xの 最大・最小を
求めるんですが
=kと置いて
式を ちょっと 書き換えると
kは
y切片で
出てくるとわかるので

09
y=-2x+kを
領域を通る様に
( x、y) が 領域内を
動くとき
kが 最大と 最小に なるとこを
見ると

10
答は こんな感じで
さっきの 横道ですが
我々世代は
息子 娘が 大人になってるか
遅かった人は
学生 真っ只中か
な感じですか
コロナの ダメージから
何とか 這い上がりたい
この頃ですね
身も 体も 心も 経済も

11
るいだい
ラーメン大学で
味噌バタ コーントッピングって
いま いくらかな
タクシー乗ってますか?
すみません
にたような 問題です

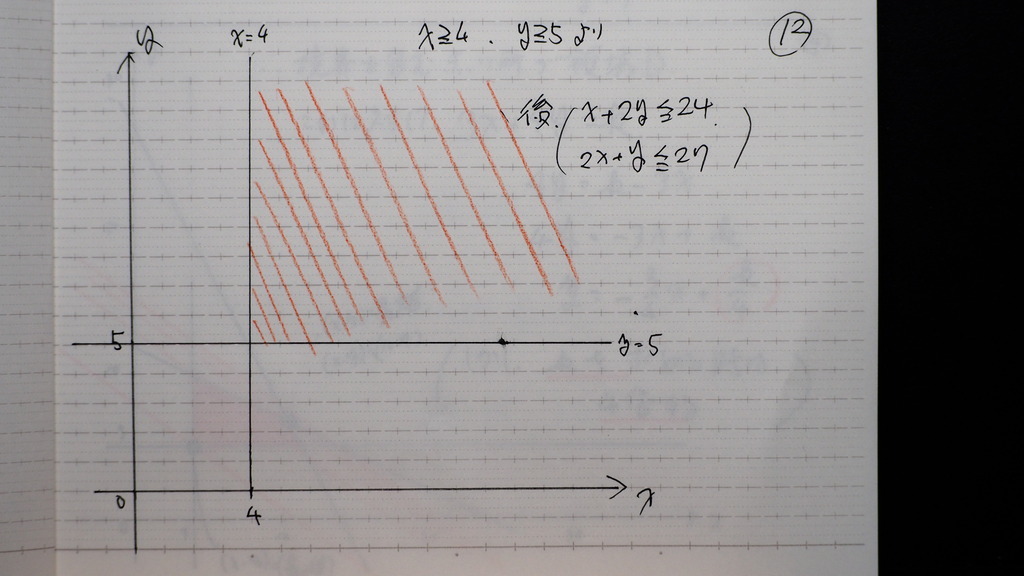
12
大雑把に ここら辺のなかの
後 二つ 不等式を
書き込むと
13
こんなだから

14
こんな感じか
ここと ここを 通るとき
最大 最小

15
数字が 偉く 大きくなってるけど
式変形したときに
最大 ・ 最小 を
求める
直線の式の y切片が
k/4 になってるので
元の 式に x、yを
代入したらば
4倍だからさ
これでいいんだけど
高校とかの 物理で
なんかの 問題を
解いていて
答が すごく おおきく 成っちゃって
せんせ 曰く 偉い 大きいな
誰か 電卓 持ってるか?
勉強するとき 別に
使ってもいいからさ
あ だいじょうぶだな

16
また 少し 横に行ってましたが
これです

17
これも 類題
領域を 求めて
最大・ 最小のとこが
表現が 変わっただけ

18
先ず 領域を
求めて
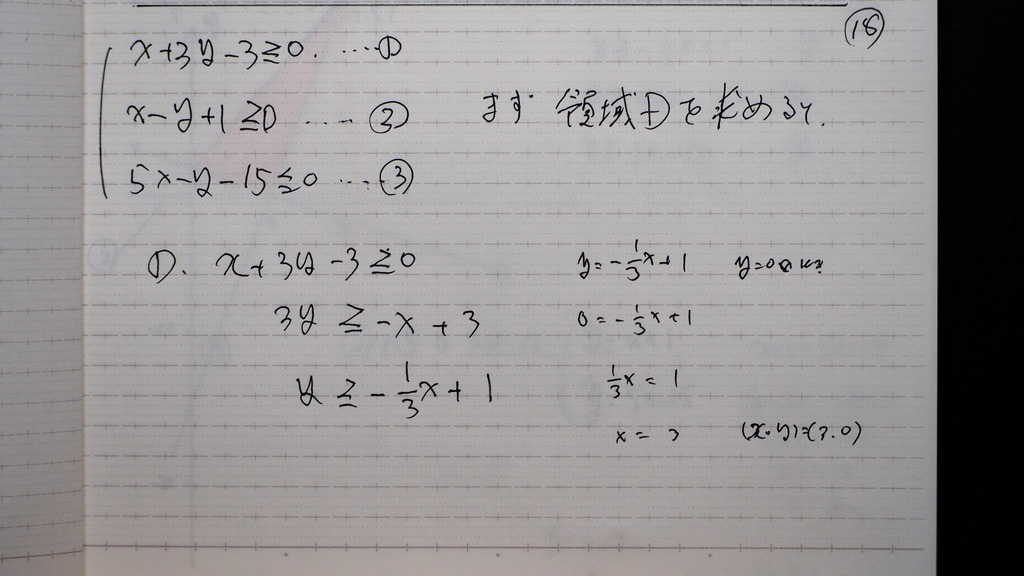
19
傾きと切片が わかる形で
グラフを 作ると
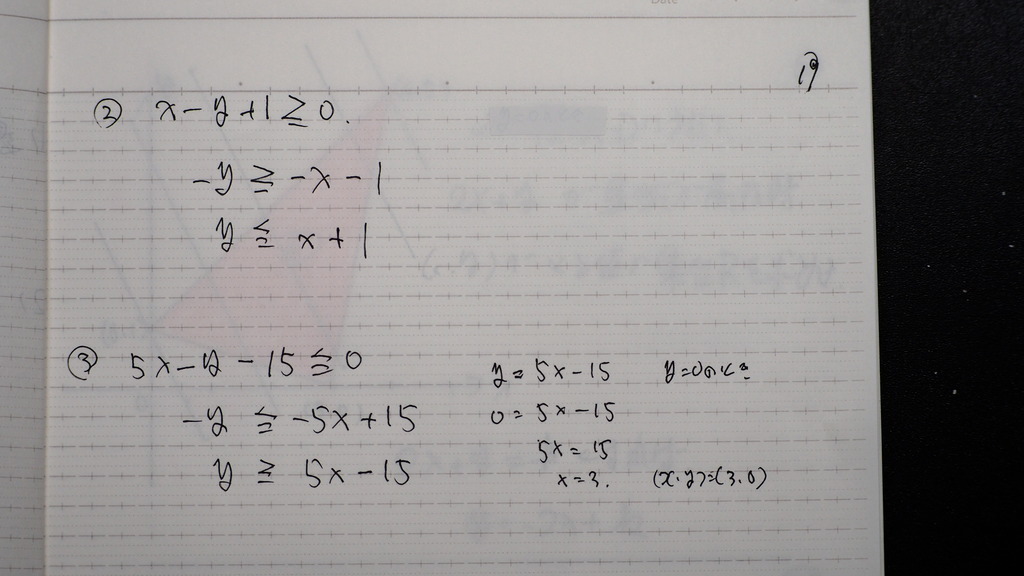
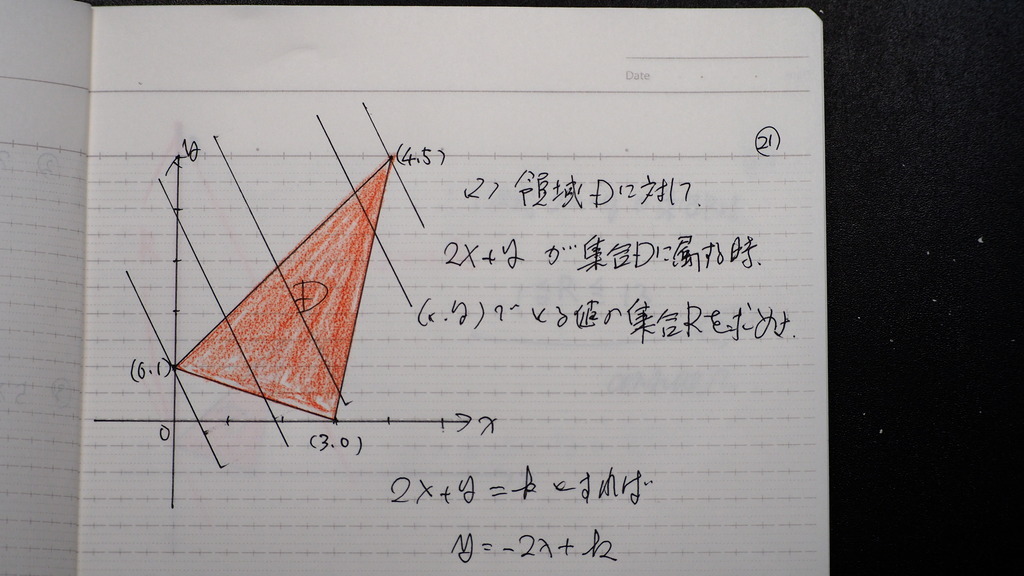
20
こんなで
②と③の 交点は(4,5)
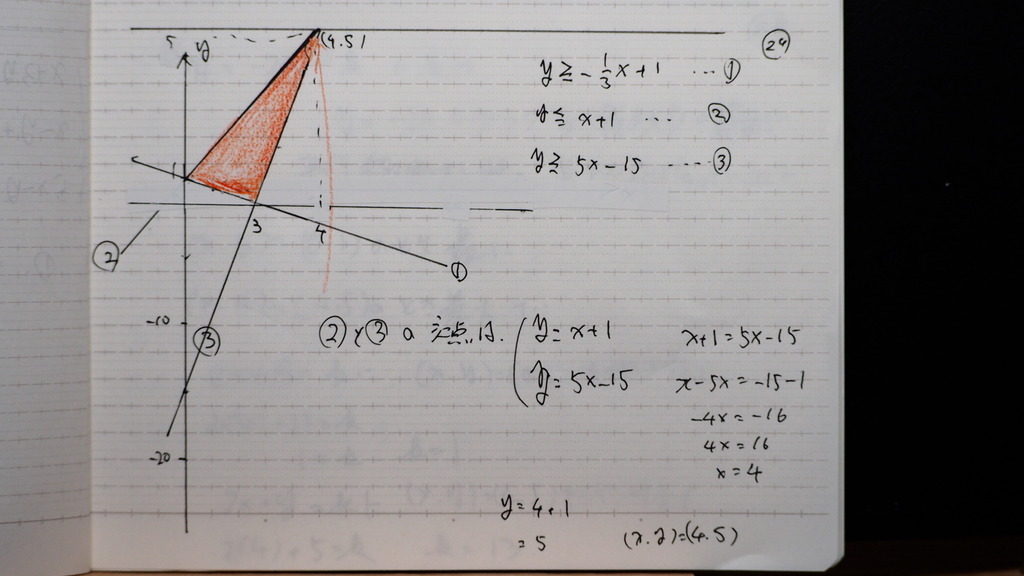
21
一次 式に領域の (x、y)を
代入してくと
y切片が
変わってくる
その 軌跡が y軸に できるんですが
それが R じゃナイスカ
22
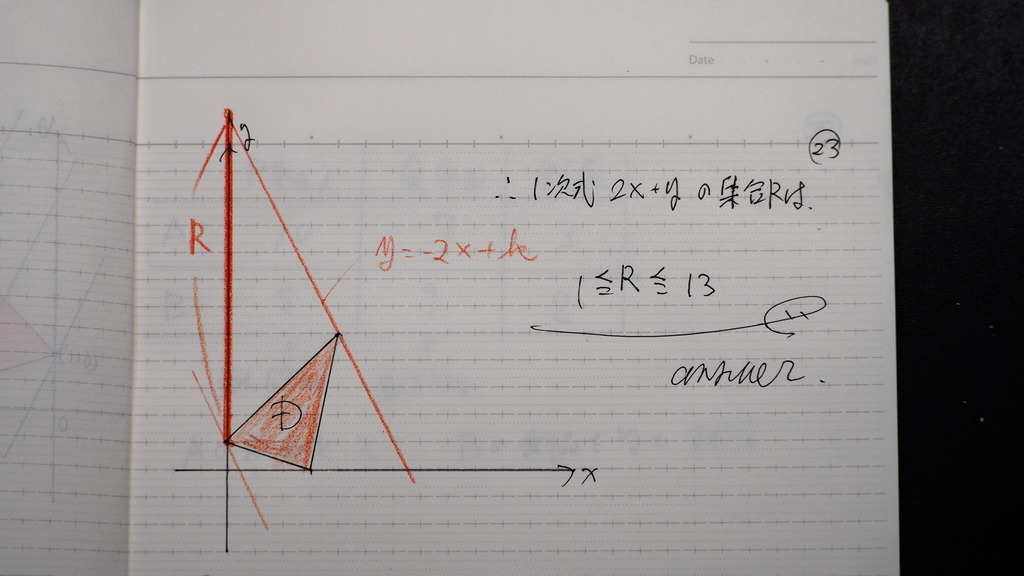
ここから ここまでを
計算して

23
こんな感じで
集合R だから R{ t | 1 レスザンイコール t レスザンイコール 13}
って書かないといけない。
24
ある工場で
製品を 2種類作っているんだって
ソレゾレ 同じ2つの原料を
割合を 変えて 作っていて
1単位作るのための 必要度と
利益は
表のようになっているんだって
最大利益を
出すには
ソレゾレ 何単位づつ
作ったらよいか

25
これがさ
表

26
表を 縦に見て
A と Bで
Pは 65キログラム
Qは 84キログラム
まで
利益を kとすれば

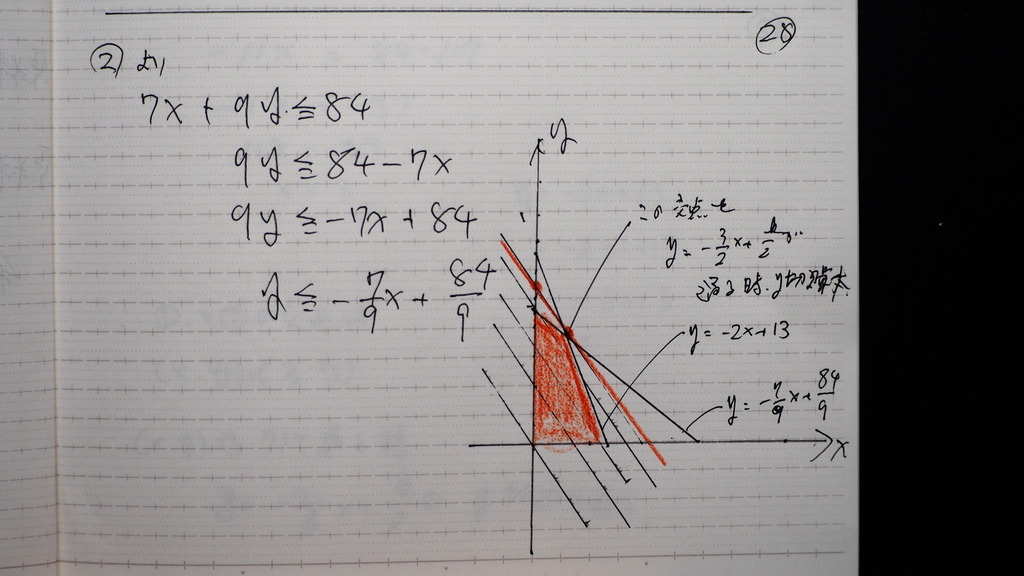
27
グラフにして

28
最大 利益を 出すには
2つの式の 交点になってるとこの
x、y の 値を
代入すると
29
交点は
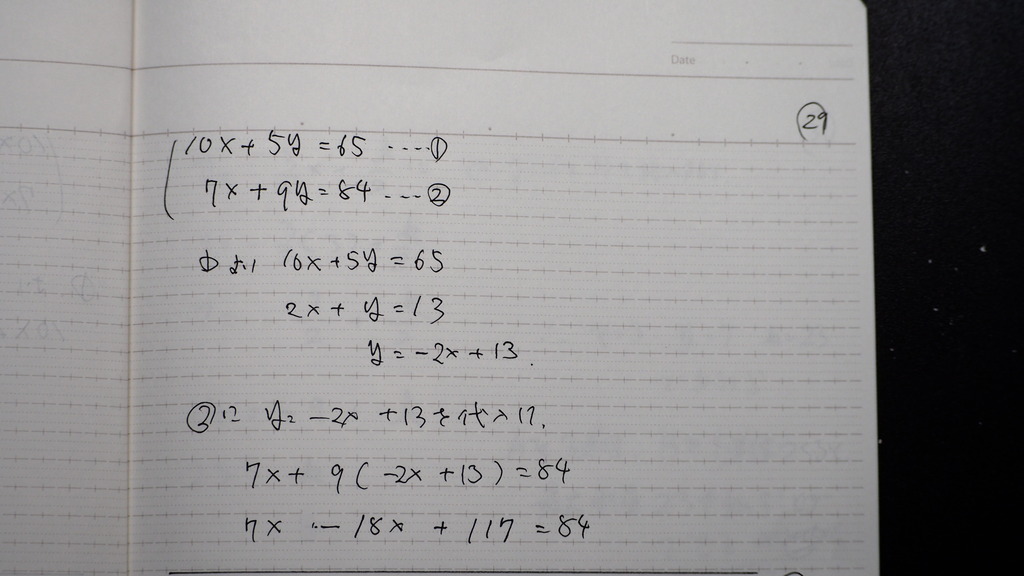
30
(3,7)
であるので
xは A yはB
としたので
Aを3単位 Bを7単位
作ると
最大利益になる

31
こんな感じですか

お疲れ様です。
図形と方程式 領域での最大・最小
01
領域を 表す式が与えられていて
その領域内を
点(x、y)が 動くとき
y+2xの 最大 ・ 最小を
求めてちょうだい。
02
まず 領域を 見える様に
絶対値が 苦手な方も
けっこう いらっしゃいますが
慣れだからさ
絶対値が ついてるがために
答は 正なんですが
絶対値が付いてないと
中味がじゃナイスカ
負の時と 正の時があるですので
03
少し整理して
04
こんな感じに
05
さらに 少し整理して
傾きと y切片が わかる形にして
06
わたしんとこは
子供は
学校も出ずに
毛皮を着て
猫っていうんですが
9匹のメス
07
話を 元に戻して
こんな感じに
整理できました
これが
与式の 表す領域ですよ
08
ここから
y+2xの 最大・最小を
求めるんですが
=kと置いて
式を ちょっと 書き換えると
kは
y切片で
出てくるとわかるので
09
y=-2x+kを
領域を通る様に
( x、y) が 領域内を
動くとき
kが 最大と 最小に なるとこを
見ると
10
答は こんな感じで
さっきの 横道ですが
我々世代は
息子 娘が 大人になってるか
遅かった人は
学生 真っ只中か
な感じですか
コロナの ダメージから
何とか 這い上がりたい
この頃ですね
身も 体も 心も 経済も
11
るいだい
ラーメン大学で
味噌バタ コーントッピングって
いま いくらかな
タクシー乗ってますか?
すみません
にたような 問題です
12
大雑把に ここら辺のなかの
後 二つ 不等式を
書き込むと
13
こんなだから
14
こんな感じか
ここと ここを 通るとき
最大 最小
15
数字が 偉く 大きくなってるけど
式変形したときに
最大 ・ 最小 を
求める
直線の式の y切片が
k/4 になってるので
元の 式に x、yを
代入したらば
4倍だからさ
これでいいんだけど
高校とかの 物理で
なんかの 問題を
解いていて
答が すごく おおきく 成っちゃって
せんせ 曰く 偉い 大きいな
誰か 電卓 持ってるか?
勉強するとき 別に
使ってもいいからさ
あ だいじょうぶだな
16
また 少し 横に行ってましたが
これです
17
これも 類題
領域を 求めて
最大・ 最小のとこが
表現が 変わっただけ
18
先ず 領域を
求めて
19
傾きと切片が わかる形で
グラフを 作ると
20
こんなで
②と③の 交点は(4,5)
21
一次 式に領域の (x、y)を
代入してくと
y切片が
変わってくる
その 軌跡が y軸に できるんですが
それが R じゃナイスカ
22
ここから ここまでを
計算して
23
こんな感じで
集合R だから R{ t | 1 レスザンイコール t レスザンイコール 13}
って書かないといけない。
24
ある工場で
製品を 2種類作っているんだって
ソレゾレ 同じ2つの原料を
割合を 変えて 作っていて
1単位作るのための 必要度と
利益は
表のようになっているんだって
最大利益を
出すには
ソレゾレ 何単位づつ
作ったらよいか
25
これがさ
表
26
表を 縦に見て
A と Bで
Pは 65キログラム
Qは 84キログラム
まで
利益を kとすれば
27
グラフにして
28
最大 利益を 出すには
2つの式の 交点になってるとこの
x、y の 値を
代入すると
29
交点は
30
(3,7)
であるので
xは A yはB
としたので
Aを3単位 Bを7単位
作ると
最大利益になる
31
こんな感じですか
お疲れ様です。
2023年04月14日
08033 大人のさび落とし 図形と方程式 図形の通る範囲
大人のさび落とし
図形の通る領域
01
yの2次関数があるんですが
変数aが 入っています
aが 実数の 値を とって
変化するとき
放物線の 通る範囲を
求めなさい

02
考え方なんですが
例えば (1,3) は通るかな
代入するでしょ
すると

03
aの値が 2つ 出て来て
-2 または 1 のとき
aが実数の値を とって
変わる とき
-2,1 になるときは
点(1,3)を 通るってことですよ
つまり
(1,3) は 通る範囲にある

04
(2,1) ならどうか
代入してみたらば
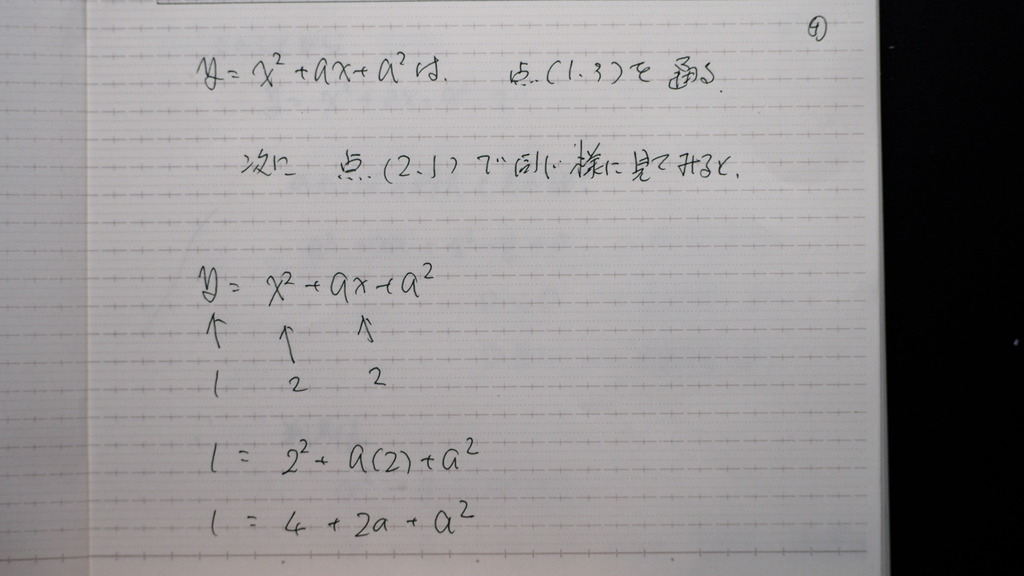
05
aの解が 虚数になった
実数でない
つまり
点(2,1) を 通るためには
aが 実数の範囲を
越えてしまうので
ダメ
通らない

06
このことから
(x、y) に 点の値を
代入して
つまり aの2次方程式にして
その解が
実数解を持つならば
通る
虚数解ならば
通らない
aの2次方程式に
整理して
判別式
Dは x、yの 関係式になっていて
Dが 0以上になれば 通る

07
こんな感じに
08
じゃあ 行きますよ
今度は
この直線が
通らない領域を
図示せよ
具体的に
(x、y) を 入れてくなんて
場合を 尽くすことは
出来ませんので
しかし
x、y が わかってるときは
この式は
aの 2次方程式になるよ
そこで
展開して
aの2次方程式に 整理して
判別式:D
D 0未満を求めると
x、yの 関係式で出て来て

09
円の 方程式になるかな

10
これで 終わりでは無くて
いま さっときてしまったけど
2次方程式でないと
判別式は 使えない
イマのは xが 2でない場合

11
xが 2の時は
2次方程式にならず
ya=-1
aは 変化する実数で
aの値が 変わっていく時に
この式が 成り立つものがあれば
通ることになる
通らない場合であるので
y=0

12
こんな感じで
13
次は
直線が
通る領域を 図示せよ
aについての
2次方程式に整理して
判別式で

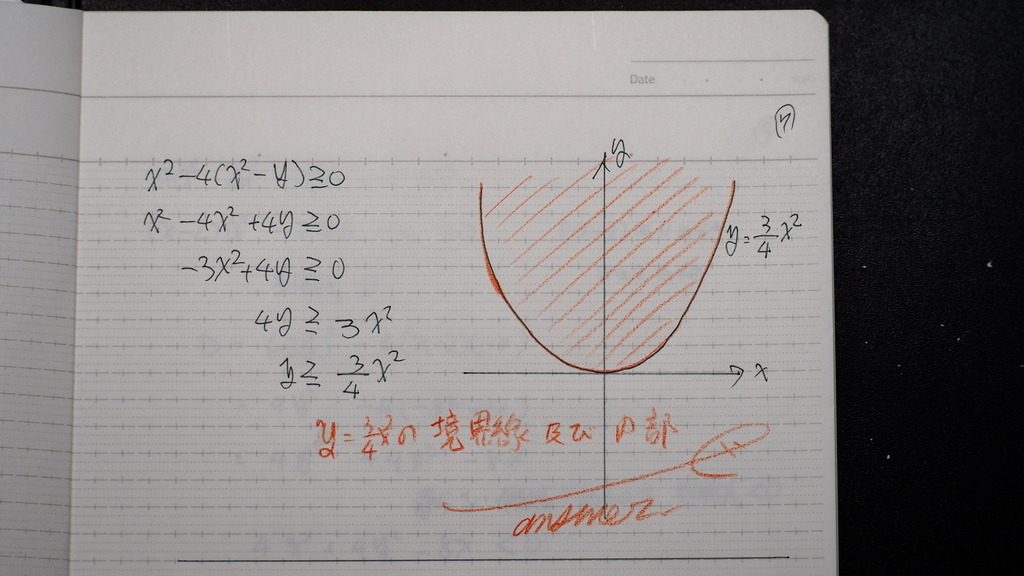
14
こんなグラフか
で グラフの 下側
って やりたいとこですが
これでは 不完全
aが 正の数の時
を どう表現するか?
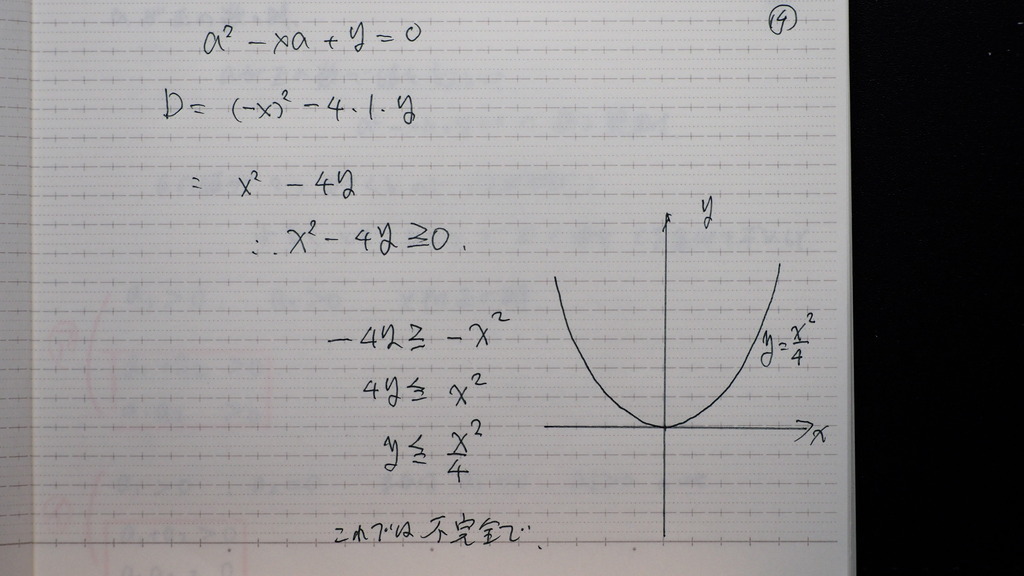
15
aについて 解くと
解が2つ 出てくるんだね
a1,a2
とするでしょ

16
aが 正の数で 値を 変える時
2次方程式なので
解が aの値が 2つある
少なくとも 1つが
正の数で あるためには
ア 2つとも正
イ どちらかが正で 他方が ゼロ

17
ウ 異符号の時
アから見てきますと
a1+a2 は 正
xは 正

18
a1a2 は 正
yは 正
であるから
赤枠
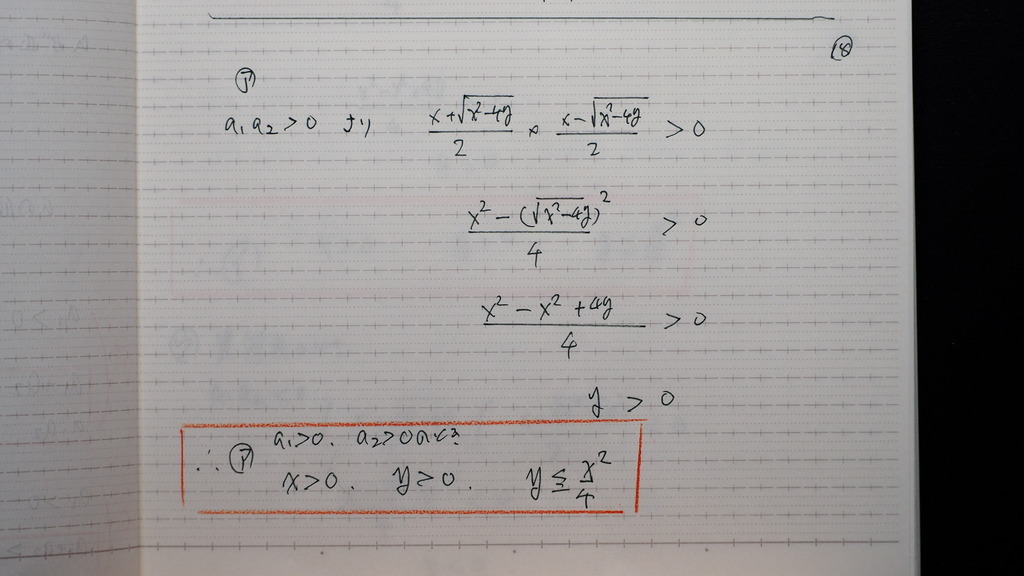
19
イ どちらかが 正で
他方が ゼロ
足せば 正
xは 正
かければ ゼロ

20
yは ゼロ
ウ のとき
掛ければ
yは 負
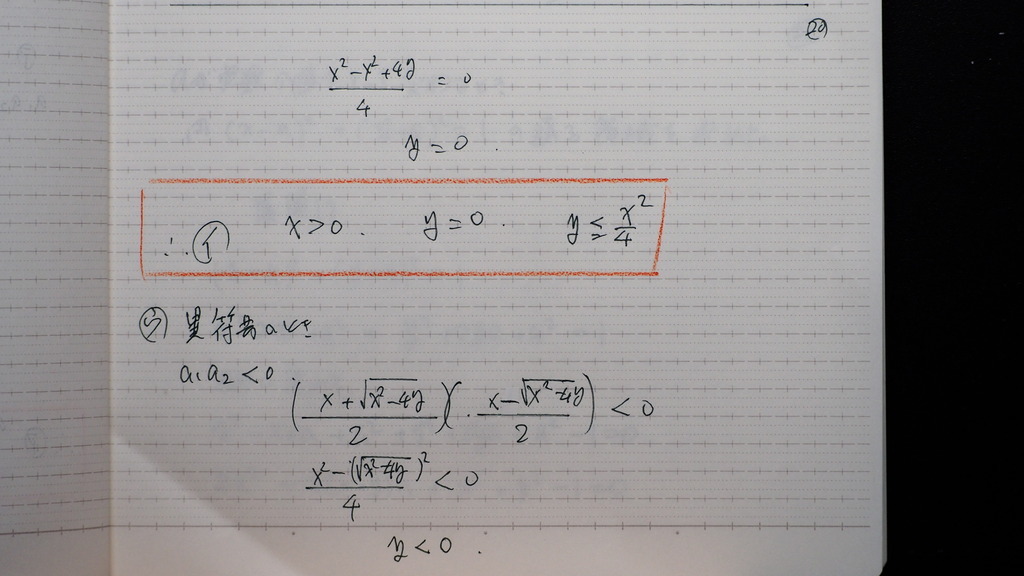
21
ア+イ+う は
こんな感じで
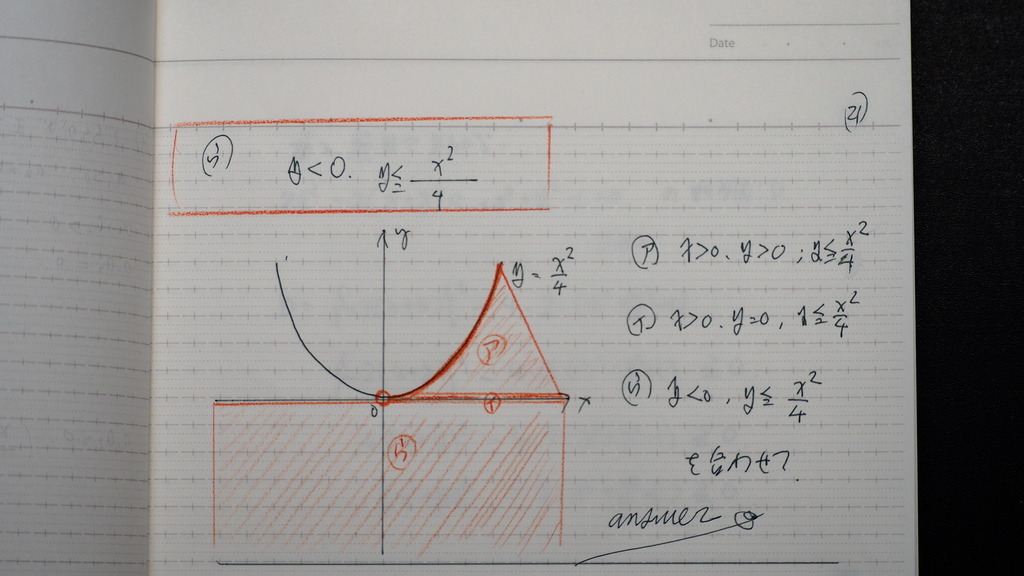
22
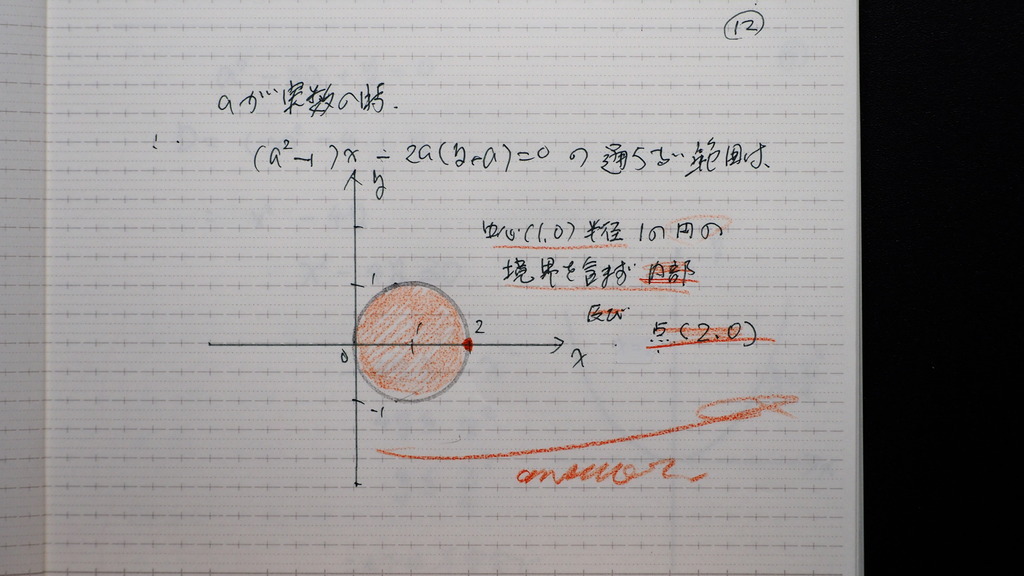
円があるんですが
aが 実数の値を
とってかわるとき
円の 通る 領域を求めよ
展開して
aで整理して

23
判別式が
ゼロ 以上のとこは
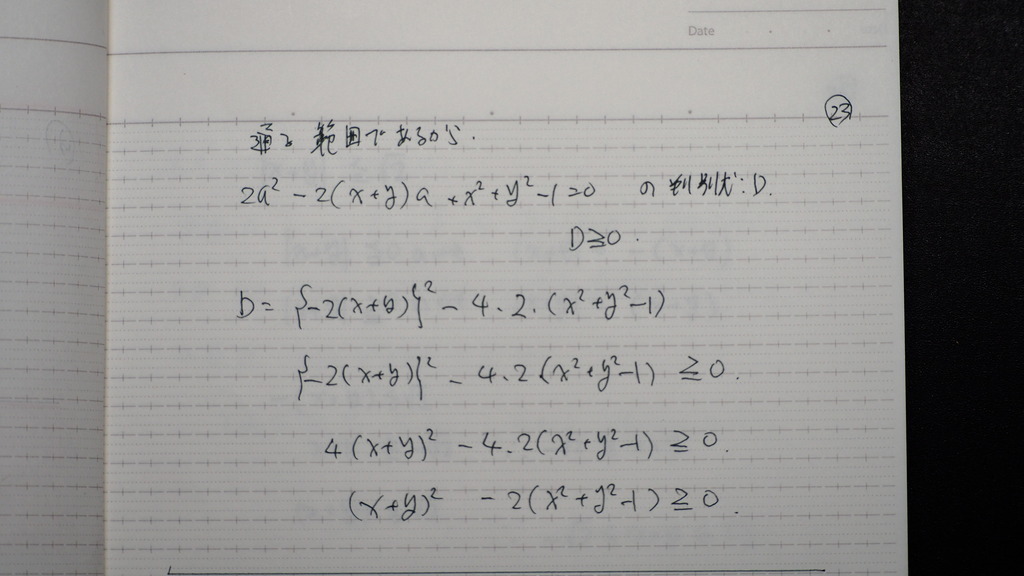
24
今回は
(x+y)の 二乗は
プラスだけど
(x+y)は マイナスの場合も
あるので
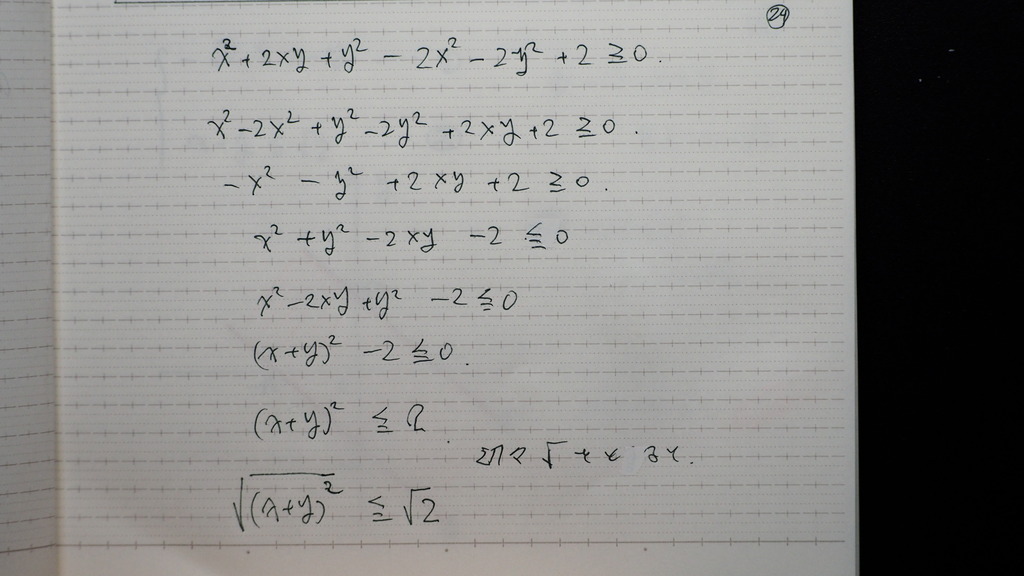
25
こうすればさ
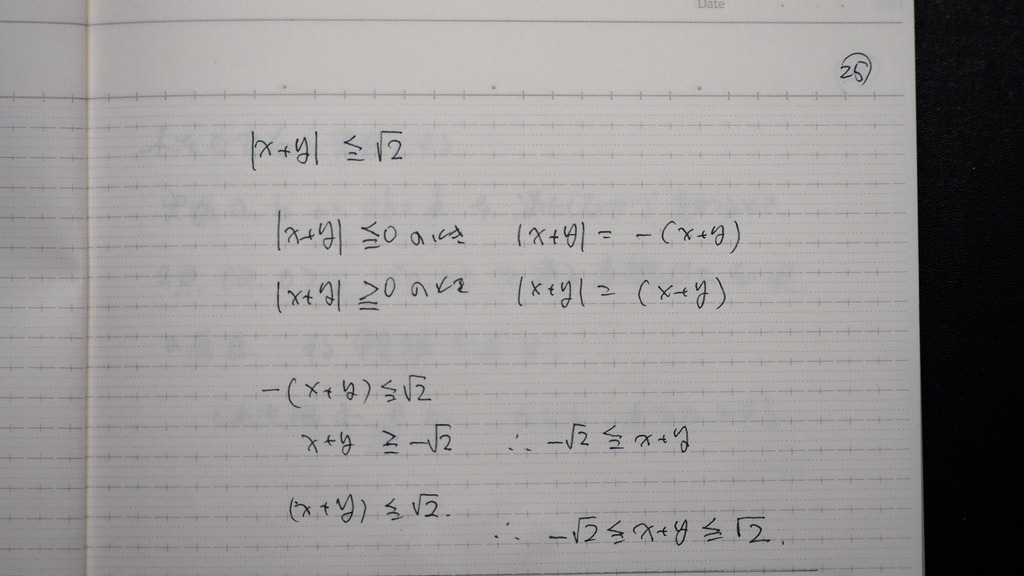
26
こんな感じで
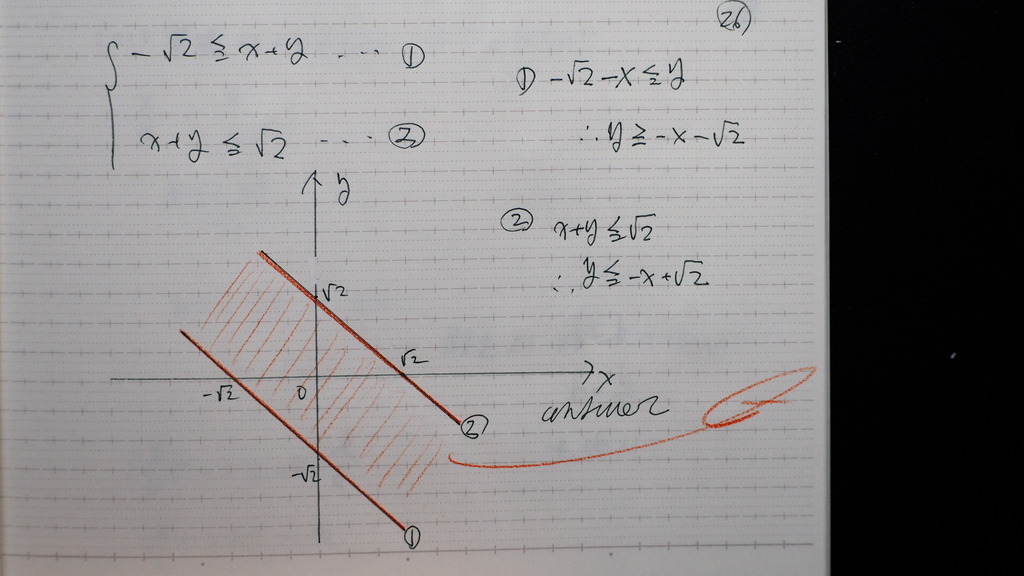
27
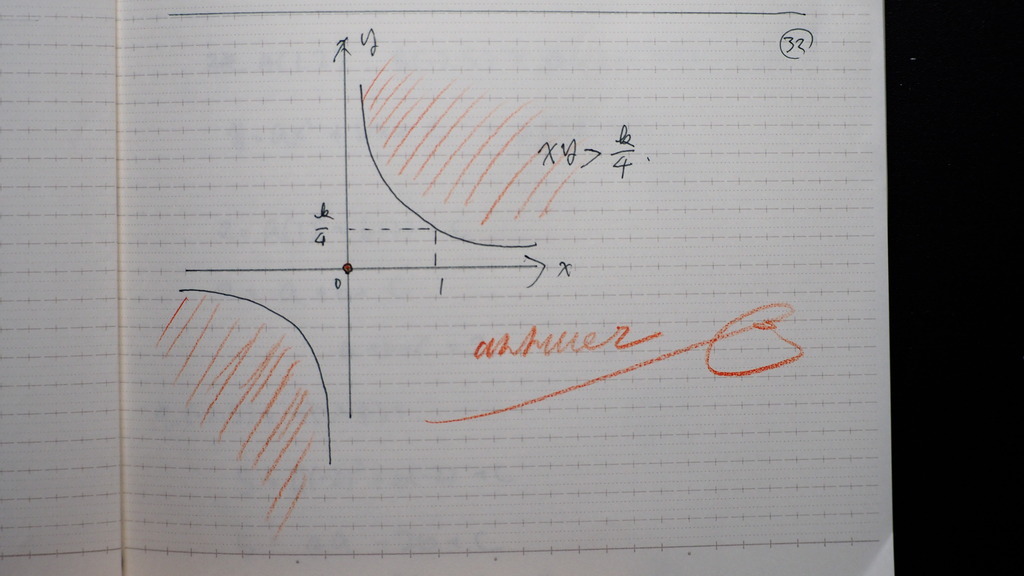
条件が いくつかあるんですが
2点を 通る直線上に 無い領域は?

28
今回の直線の 方程式は
両切片型なので
あったじゃナイスカ
こんな感じで
これを
平らにしてくと

29
実数変数のa,bを
aで表してるので
aの 2次方程式の 判別式にして
2次の項の係数yが
ゼロでないとき

30
方曲線の感じに
なってじゃナイスカ

31
2次の項の係数yが
ゼロの時
x=aで これは ゼロではない
逆に
このとき
y=0のとき X=0は 通らない

32
こんな感じですか
33
直交座標において
点A(1,2)、B(-2,5)を通る
どんな 2次曲線も
決して 通らない 点
を 求めよ

34
a,b,cを 全部 aで
表わせば
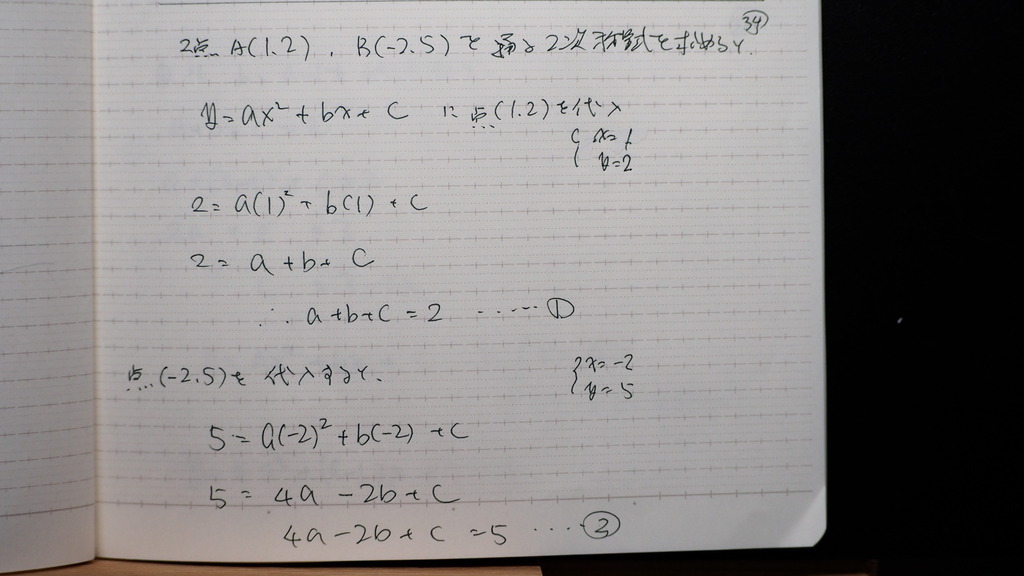
35
先ずb
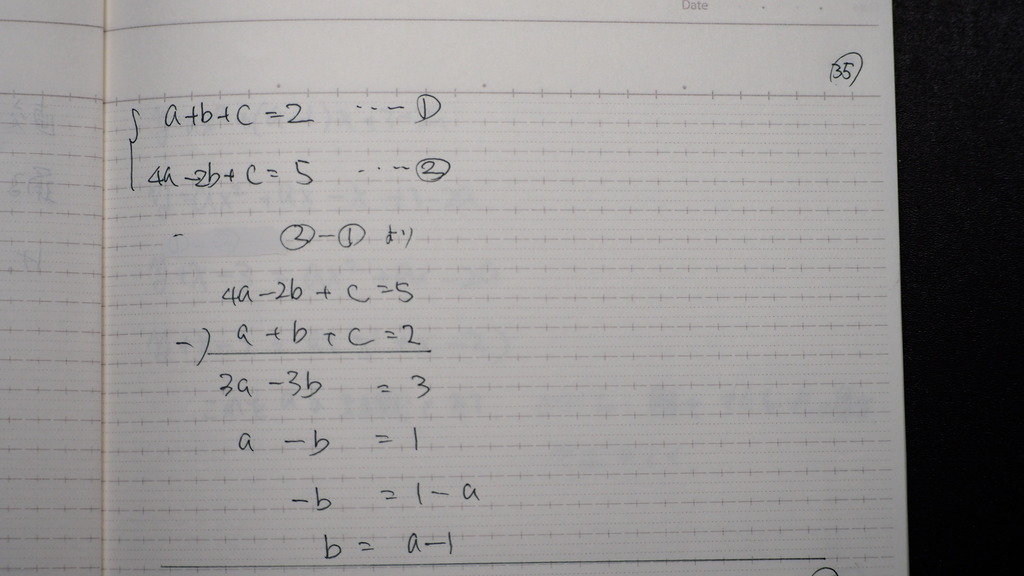
36
つぎにc
b、cを 代入して
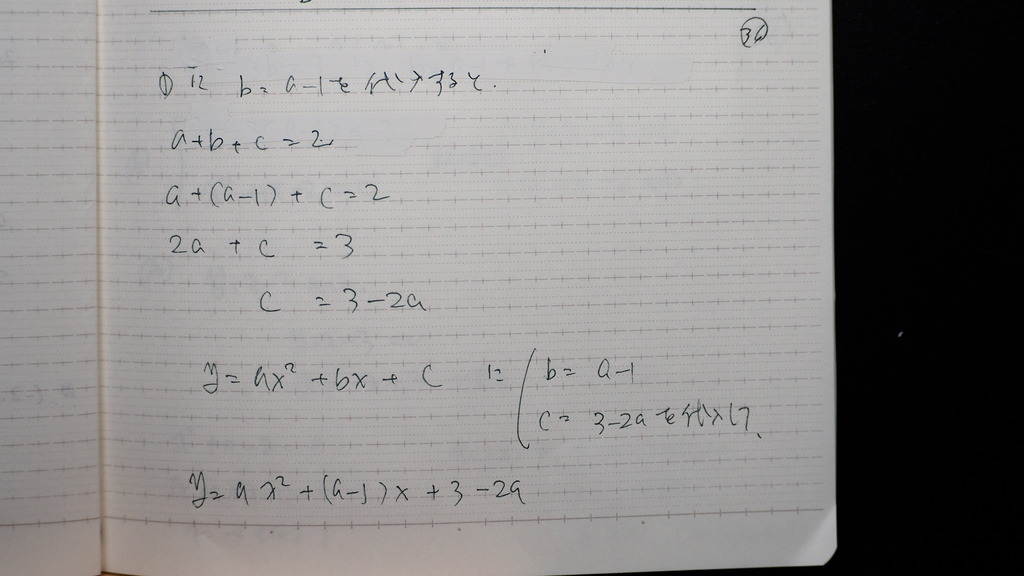
37
ここからなんですが
これを
aの方程式と考えて
ゼロでない
解を
持たない 点の集合を
求めると

38
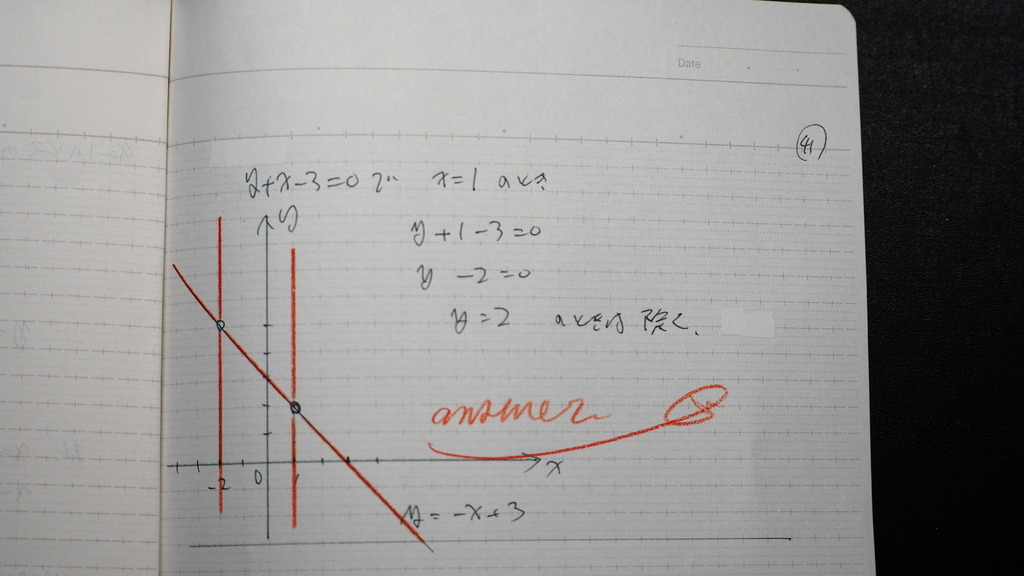
Ⓐ y=-x+3 ではない
もう一つの 式から
x=-2の時 y=5は
解になってしまうので
外す
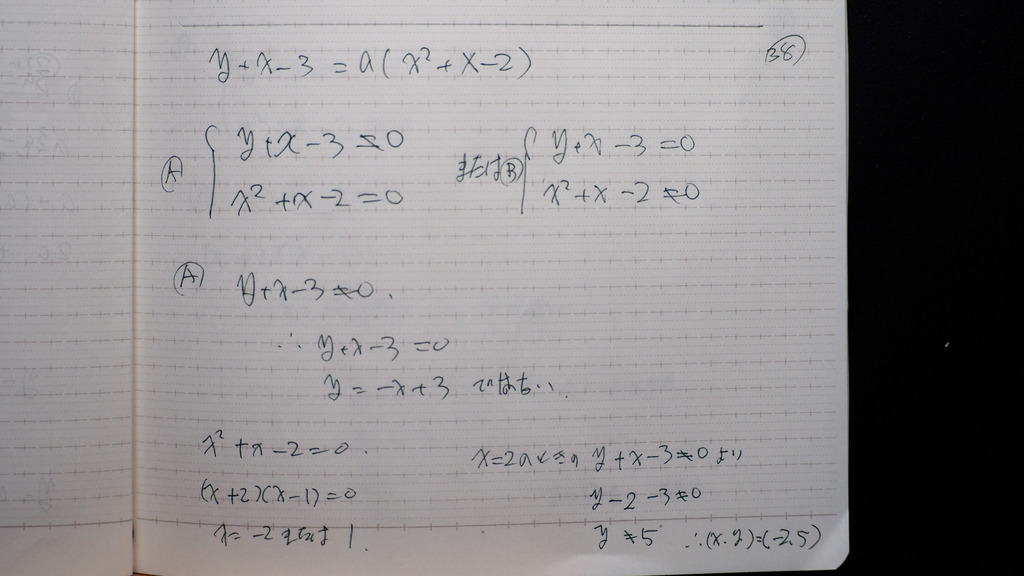
39
x=1の時
y=2は 解になってしまうので
外す

40
Ⓑも 見てみた結果

41
こんな感じで
赤い所
お疲れ様です。
図形の通る領域
01
yの2次関数があるんですが
変数aが 入っています
aが 実数の 値を とって
変化するとき
放物線の 通る範囲を
求めなさい
02
考え方なんですが
例えば (1,3) は通るかな
代入するでしょ
すると
03
aの値が 2つ 出て来て
-2 または 1 のとき
aが実数の値を とって
変わる とき
-2,1 になるときは
点(1,3)を 通るってことですよ
つまり
(1,3) は 通る範囲にある
04
(2,1) ならどうか
代入してみたらば
05
aの解が 虚数になった
実数でない
つまり
点(2,1) を 通るためには
aが 実数の範囲を
越えてしまうので
ダメ
通らない
06
このことから
(x、y) に 点の値を
代入して
つまり aの2次方程式にして
その解が
実数解を持つならば
通る
虚数解ならば
通らない
aの2次方程式に
整理して
判別式
Dは x、yの 関係式になっていて
Dが 0以上になれば 通る
07
こんな感じに
08
じゃあ 行きますよ
今度は
この直線が
通らない領域を
図示せよ
具体的に
(x、y) を 入れてくなんて
場合を 尽くすことは
出来ませんので
しかし
x、y が わかってるときは
この式は
aの 2次方程式になるよ
そこで
展開して
aの2次方程式に 整理して
判別式:D
D 0未満を求めると
x、yの 関係式で出て来て
09
円の 方程式になるかな
10
これで 終わりでは無くて
いま さっときてしまったけど
2次方程式でないと
判別式は 使えない
イマのは xが 2でない場合
11
xが 2の時は
2次方程式にならず
ya=-1
aは 変化する実数で
aの値が 変わっていく時に
この式が 成り立つものがあれば
通ることになる
通らない場合であるので
y=0
12
こんな感じで
13
次は
直線が
通る領域を 図示せよ
aについての
2次方程式に整理して
判別式で
14
こんなグラフか
で グラフの 下側
って やりたいとこですが
これでは 不完全
aが 正の数の時
を どう表現するか?
15
aについて 解くと
解が2つ 出てくるんだね
a1,a2
とするでしょ
16
aが 正の数で 値を 変える時
2次方程式なので
解が aの値が 2つある
少なくとも 1つが
正の数で あるためには
ア 2つとも正
イ どちらかが正で 他方が ゼロ
17
ウ 異符号の時
アから見てきますと
a1+a2 は 正
xは 正
18
a1a2 は 正
yは 正
であるから
赤枠
19
イ どちらかが 正で
他方が ゼロ
足せば 正
xは 正
かければ ゼロ
20
yは ゼロ
ウ のとき
掛ければ
yは 負
21
ア+イ+う は
こんな感じで
22
円があるんですが
aが 実数の値を
とってかわるとき
円の 通る 領域を求めよ
展開して
aで整理して
23
判別式が
ゼロ 以上のとこは
24
今回は
(x+y)の 二乗は
プラスだけど
(x+y)は マイナスの場合も
あるので
25
こうすればさ
26
こんな感じで
27
条件が いくつかあるんですが
2点を 通る直線上に 無い領域は?
28
今回の直線の 方程式は
両切片型なので
あったじゃナイスカ
こんな感じで
これを
平らにしてくと
29
実数変数のa,bを
aで表してるので
aの 2次方程式の 判別式にして
2次の項の係数yが
ゼロでないとき
30
方曲線の感じに
なってじゃナイスカ
31
2次の項の係数yが
ゼロの時
x=aで これは ゼロではない
逆に
このとき
y=0のとき X=0は 通らない
32
こんな感じですか
33
直交座標において
点A(1,2)、B(-2,5)を通る
どんな 2次曲線も
決して 通らない 点
を 求めよ
34
a,b,cを 全部 aで
表わせば
35
先ずb
36
つぎにc
b、cを 代入して
37
ここからなんですが
これを
aの方程式と考えて
ゼロでない
解を
持たない 点の集合を
求めると
38
Ⓐ y=-x+3 ではない
もう一つの 式から
x=-2の時 y=5は
解になってしまうので
外す
39
x=1の時
y=2は 解になってしまうので
外す
40
Ⓑも 見てみた結果
41
こんな感じで
赤い所
お疲れ様です。
2023年04月06日
08032 大人のさび落とし 領域を 表す 不等式
大人のさび落とし
領域を 表す 不等式
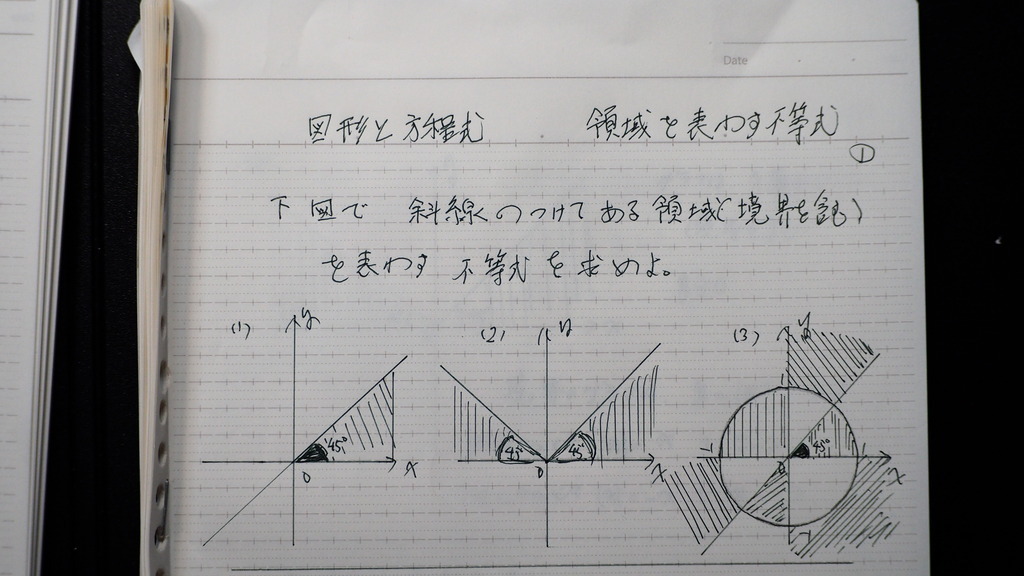
01
今回は 領域が
初めに 示されています
この領域を
表す 不等式を 求めなさい
(1)(2)は 兎も角さ
(3)は やばいよね
02
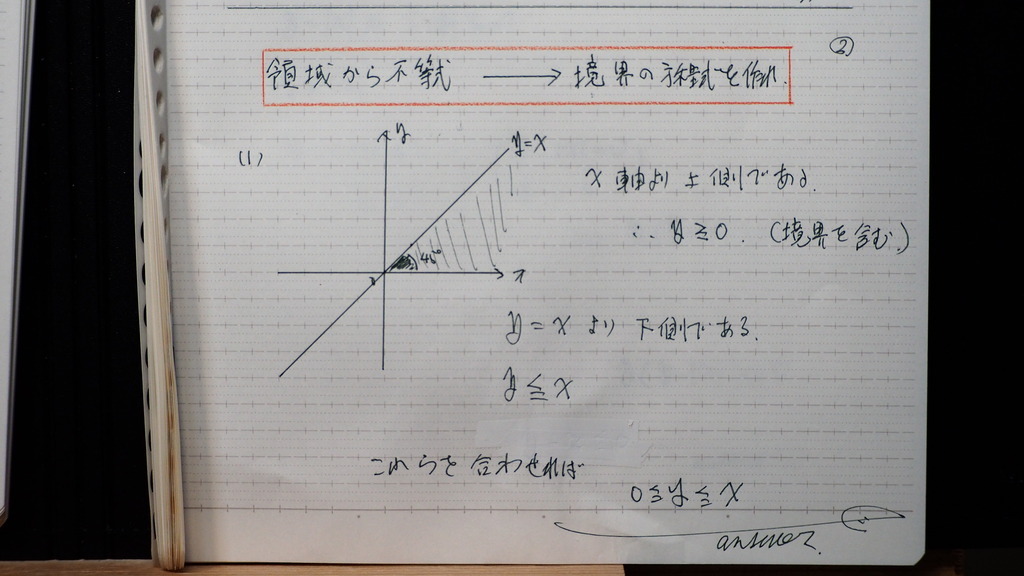
(1)は
Y=xの線を含んで 下側
と
y=0 以上の 領域
であるから
うまく くっつけられて
こんな感じで
03
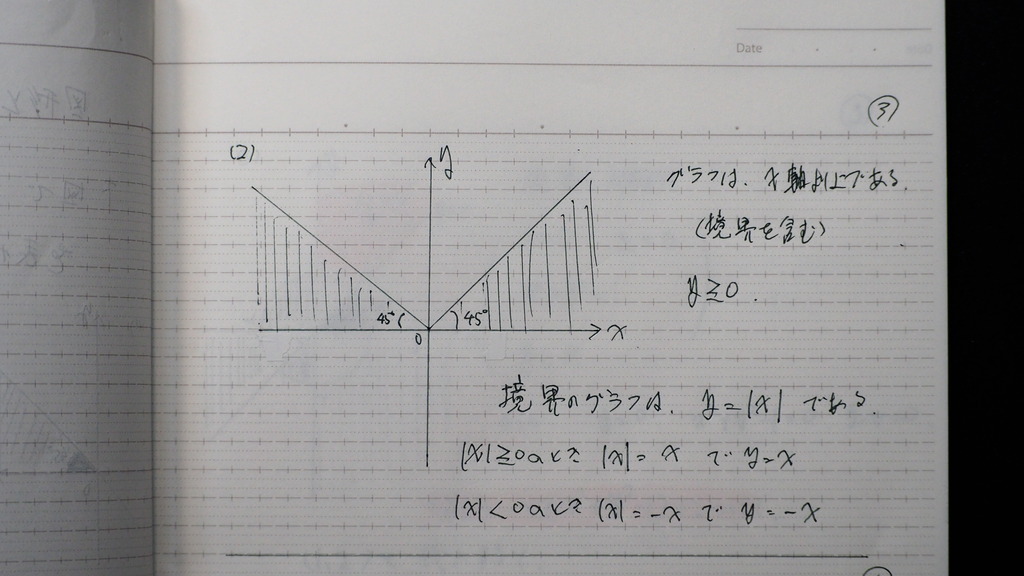
(2) これはさ
絶対値 の グラフ
04
y=0 と y=|x|
について
y=0以上
y=|x|以下
y=|x|以下は
y-|x|=0以下に 式変形して
ゼロ以下 × ゼロ以上
(マイナス) (プラス)
= ゼロ以下
(マイナス)
で
くっつけてですよ
こんな感じで
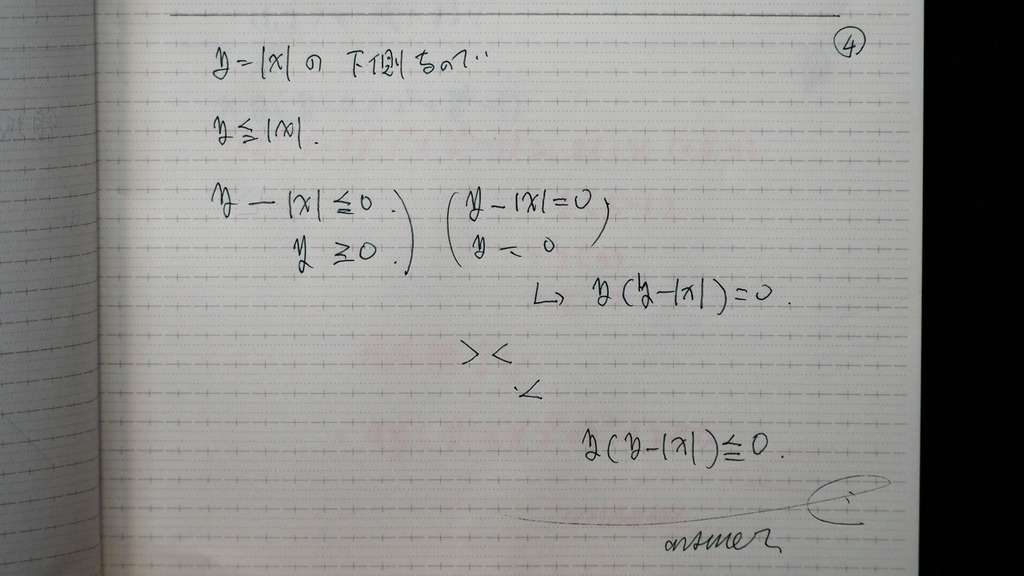
05
問題はさ
これなんだけど
境界線を一つ
越すごとに
+、-、+、-と 変わっている
境界線の方程式を
拾ってきて
=0の形にして
全部 掛け合わせてじゃナイスカ
いいんかな
領域の ひとつを 選んできて
その中の 要素を 代入したらば

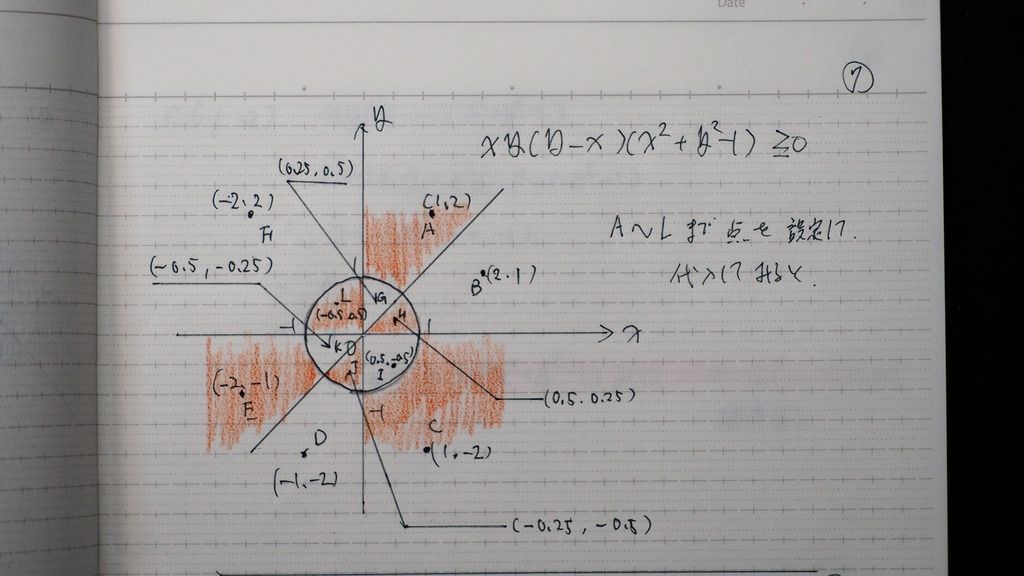
06
プラスになるんだね
そこで
境界線を 含んでいるので
=もつけて
プラス
これが 答えなんだけど

07
実際に なってるか
計算してみるとさ
08
なんか 物理かなんかの
実験データ みたいな感じだけどさ

09
交互に
+、-、になってるようですが

10
めんどうだから
電卓を たたいてると
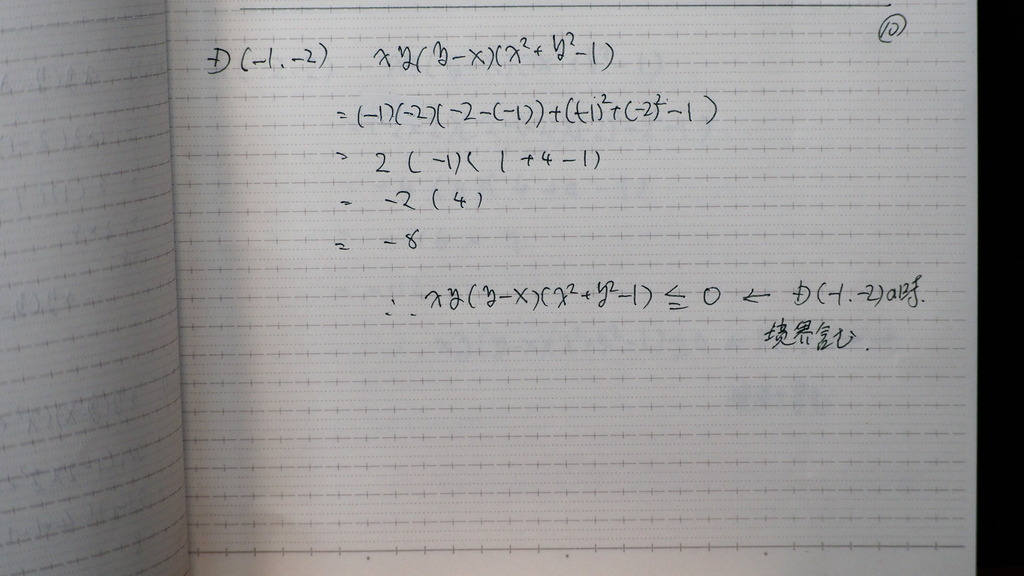
11
そういえば
実験とかで
電卓 が 必要になって
けっこう 高いの 買ってたかな
(学生の頃)

12
高校までと違って
試験のときに
電卓 持ち込み可
なんて言う試験も
ざらだし
( ただし
プログラムは 不可とかさ)
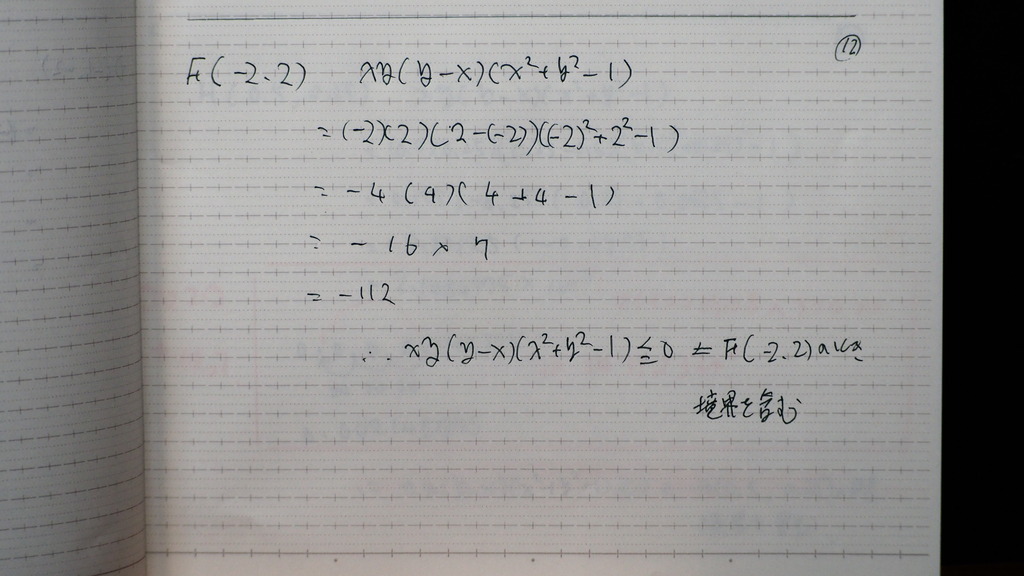
13
始めん頃
不思議な感じで
試験してましたが

14
あ コロコロ 使ってますか
電卓が ある時はいいけどさ
て計算の時に
マイナス 何乗
とかさ
マイナスの時は
左へ
今回は 3コロコロ

15
計算自体は
プラスか マイナス で
出てくるけど
境界線を 含んでますため
= も 付けてね
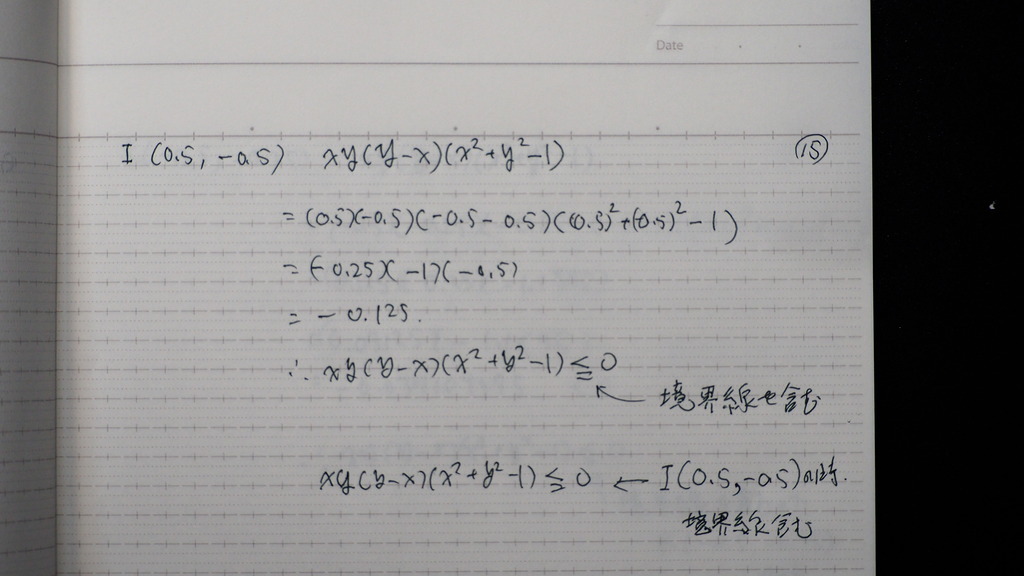
16
学生の時はさ
実験が 長引くと
学食に
行けなくて

17
よくさ
実験中に
召しが食いたい
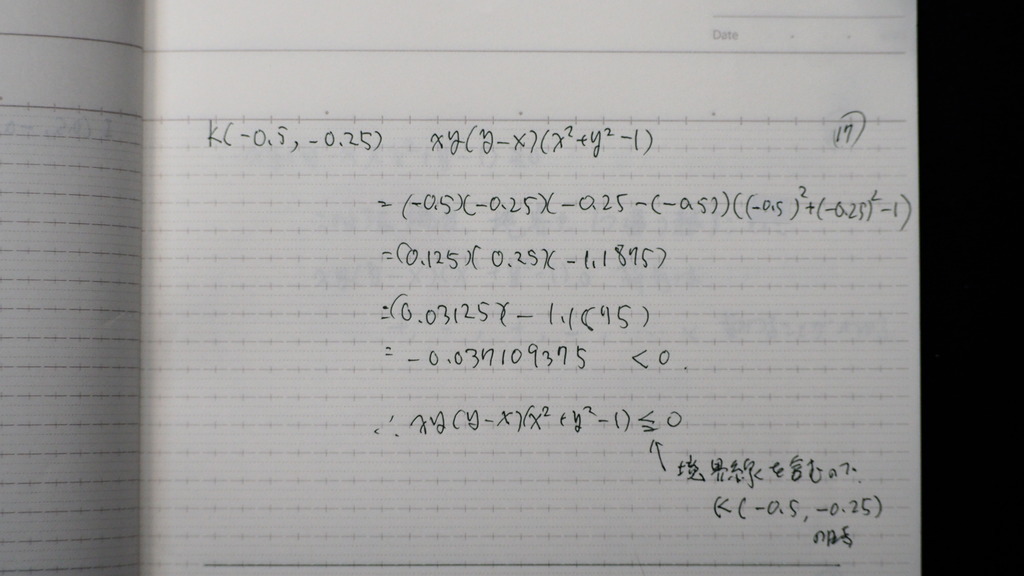
18
我々は
やらなかったけど
化学かなんかの 人たちで
実験中に
おなかがすいて
ビーカーで ラーメン煮てたとか
むかしは
良くありましたね
教授は 寛大で
やっても いいけど
チャンと 洗っときなさいよ!!
(わたしん時は まだ
インターネットが 始まったばかりで
パソコンも
カセットテープ
フロッピーディスク
が メインで
情報が 遅かった
だから 拡散されず あまり
問題にならず すんでましたが
イマハ
うっかり いたずら半分に
やっちゃうと
社会の 歯車の 一つだと
いうことを 忘れちゃうと
すぐ 大問題に なってしまうので
よく考えてじゃナイスカ)

19
そんなことは
兎も角
今回の ようなケースは
こんな感じに
なるよです

20
では 類題 行ってみましょう
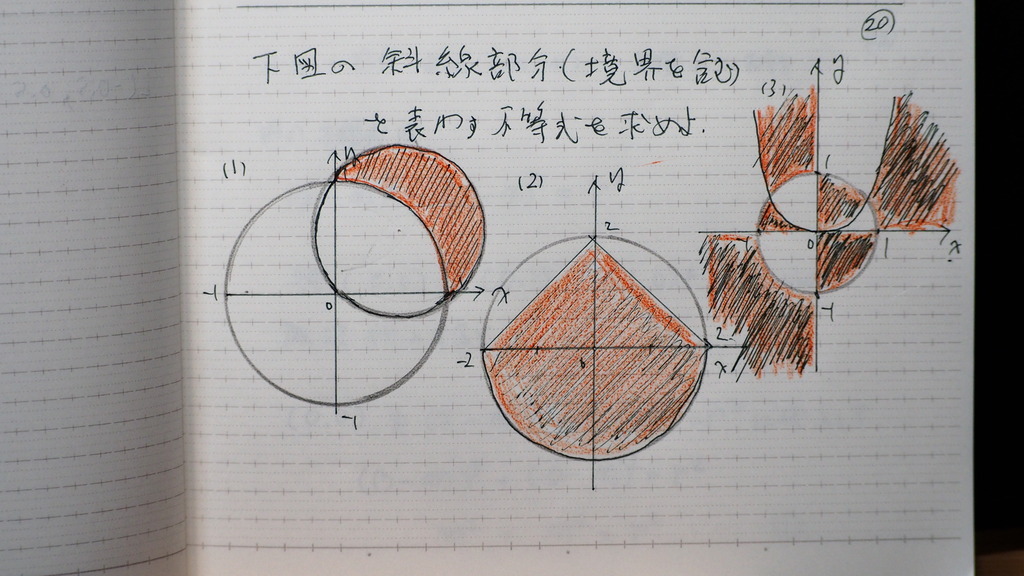
21
大きい円と
小さい円
大きい円の 外側で
カツ
小さい円の 内側
境界線含む
大きい円は 中心が (0,0)半径1

22
小さい円は
中心と 半径が わかんないけど
円周上の 3点が わかってるので
計算してみますと
まず (0,0)

23
(0,1)
(1,0)
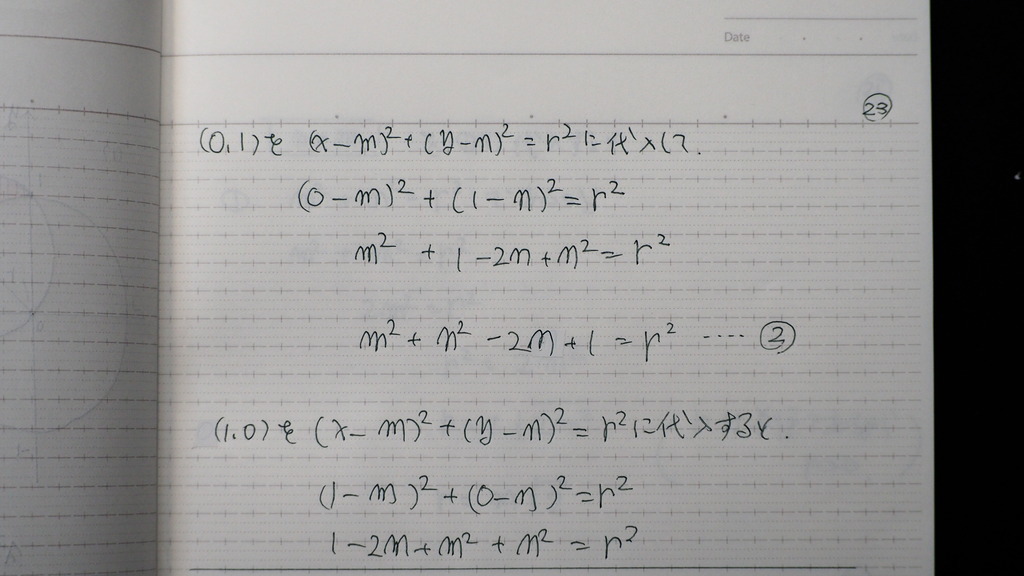
24
式が3本出て来て
②③から
n=m
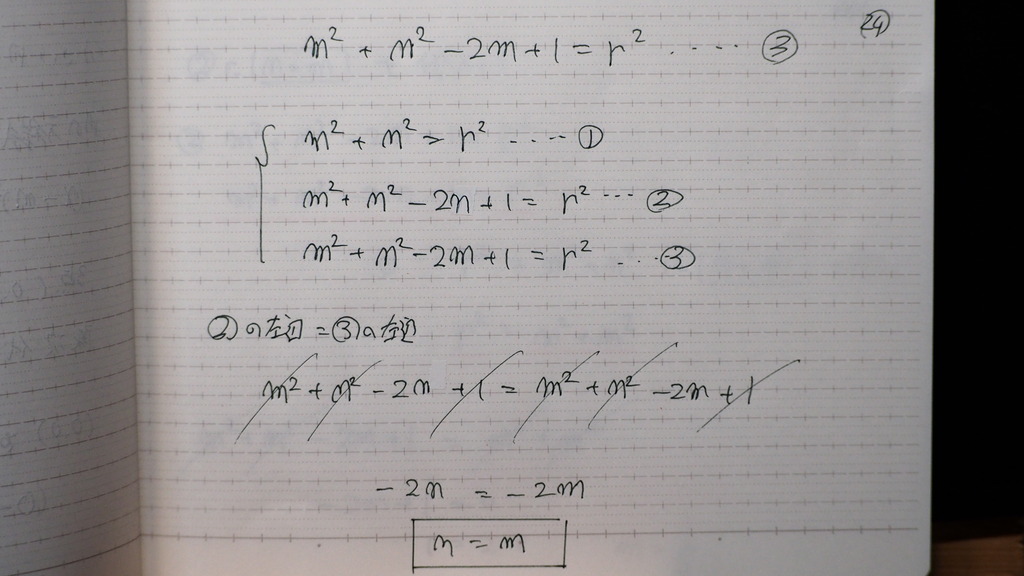
25
➀に n=mを
代入して
半径がさ
半径は 長さ であるんで
正の値

26
nと m を
全部 mにして
そうするとさ
rの二乗もさ
で
m=1/2
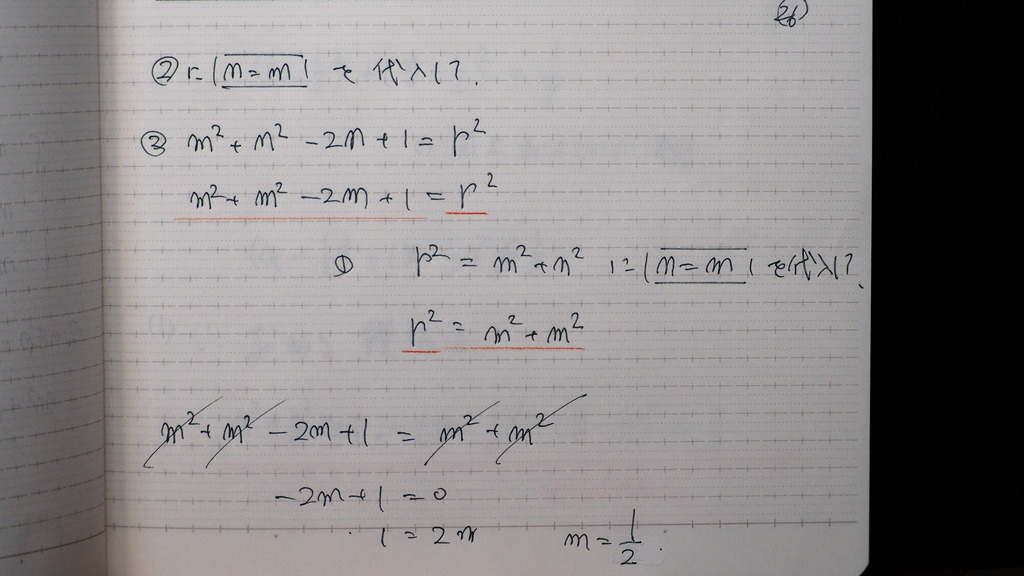
27
n、m 、rが出てきたので
方程式が出来上がって
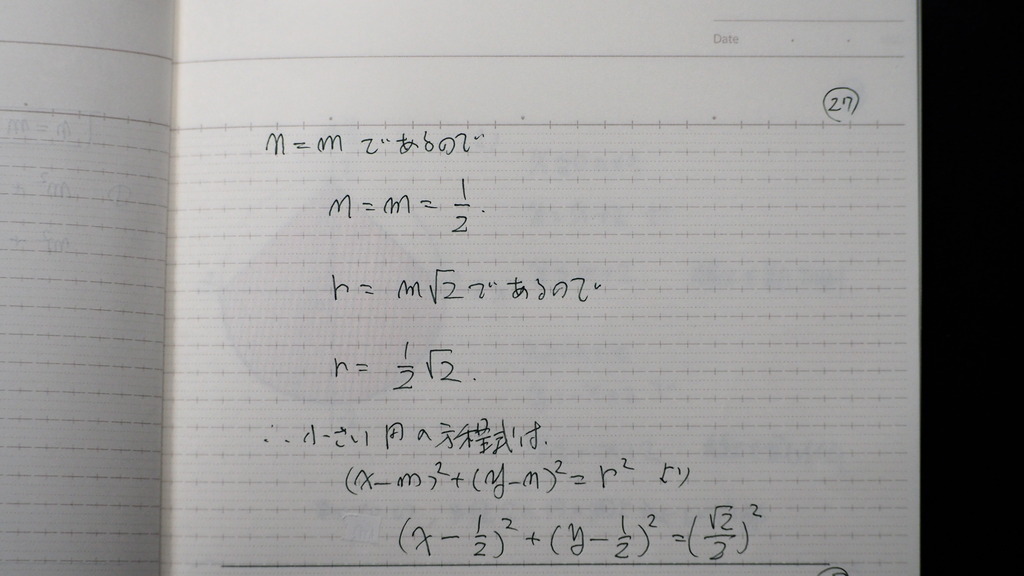
28
その 周上 および 内部
大きい円と 合わせると
こんな感じで

29
これはさ
円と 絶対値の グラフ
2本の線分と 円で 囲まれた
境界線上と 内部
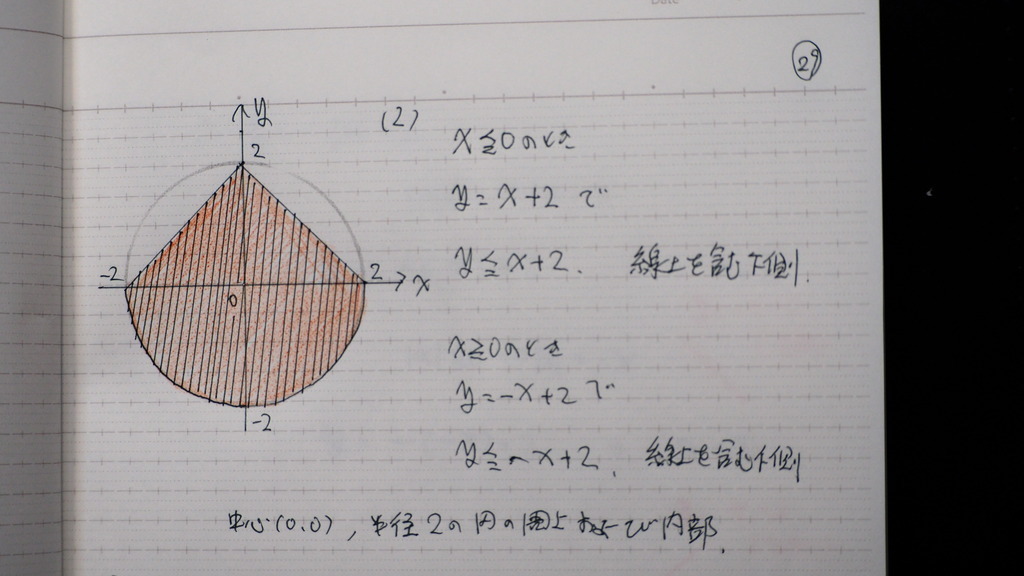
30
絶対値をさ
外すと
マイナスの時は
絶対値 ヲ 外すと 前に
マイナスが
ところが
絶対値を 外したときに
xが プラスになってるので
絶対値の前に マイナスをつけて

31
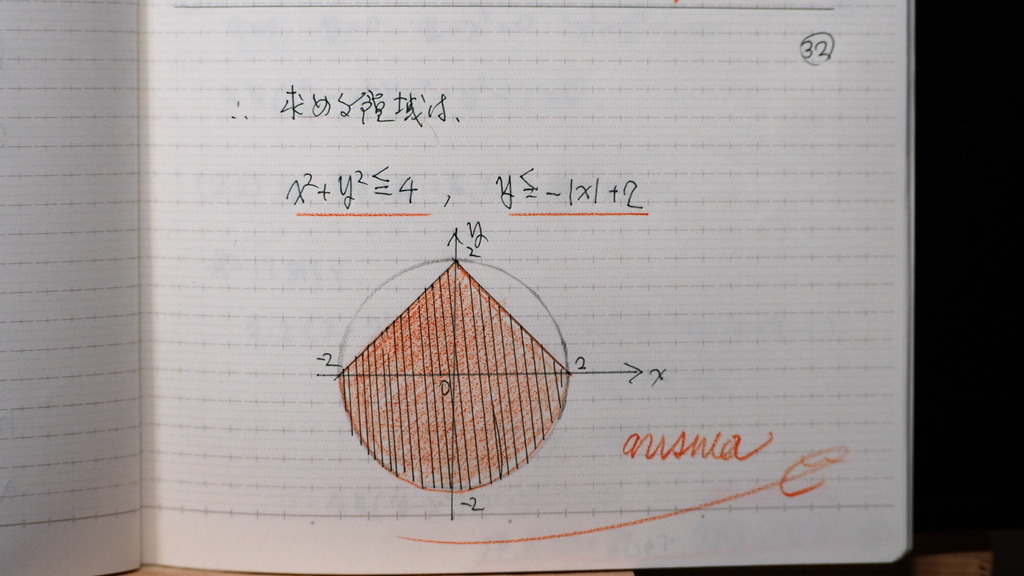
こんな感じで

32
円の方は 問題なく
であるので
こんな感じに
33
次がさ
これは
今回は 逐次 調べないけど
境界線を
一つ 越えると +、-、+、
と変わってるので
境界の方程式を
拾ってきて

34
=0に 変形して
掛け合わせて
領域になってる
エリアの 点を代入して
マイナスになったので
境界線も 含むから
=もつけて
こんな感じに

35
問題を 読んでいただいて

36
三角形を
直線の 方程式で
囲んで 行く時に
直線の 方程式は
こんなでしたね
この3番目を 使って

37
こんな感じじゃナイスカ

38
C、D、ッテいう点は
ここ と ここ
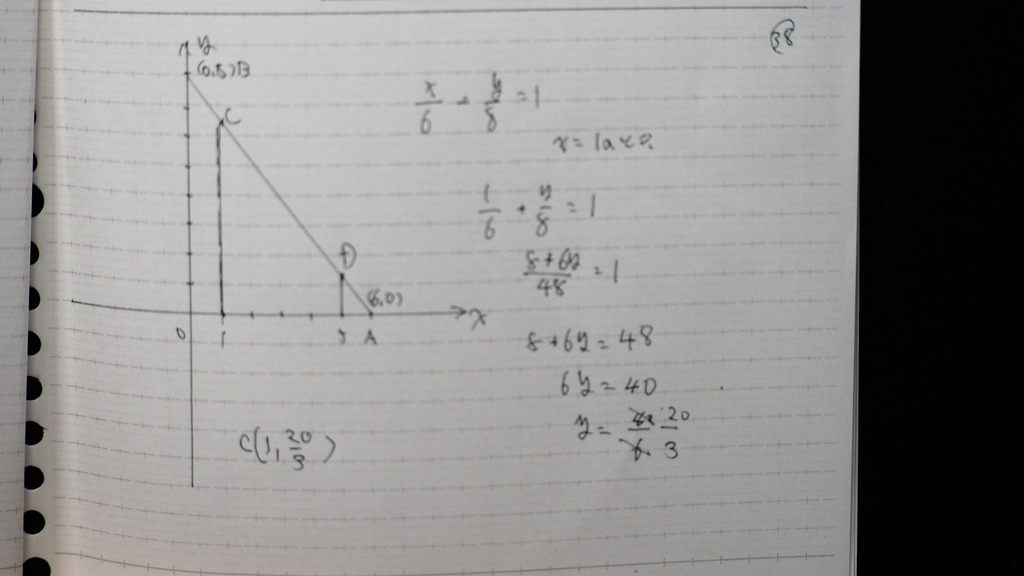
39
座標が 出てきたので
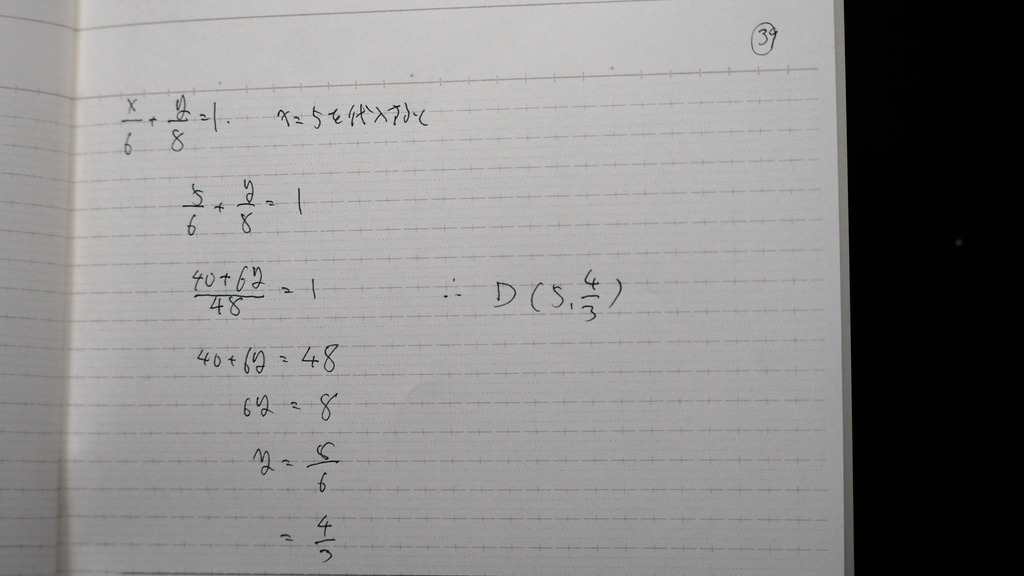
40
二次関数の グラフは
こんな感じなので
Cのときより 下
Dの時より 上
マイナス プラス かけて
マイナスになる
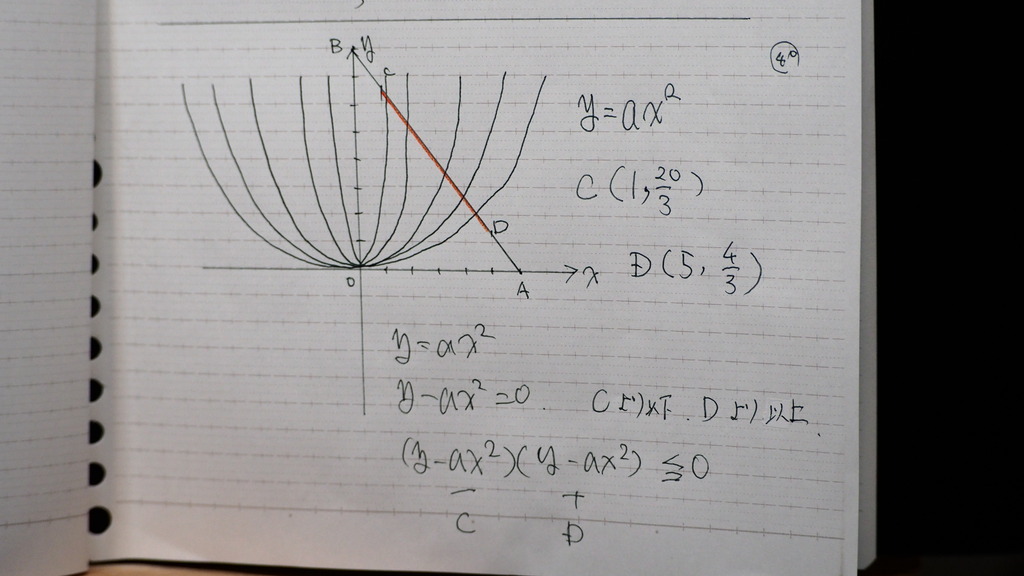
41
この不等式を
解くと
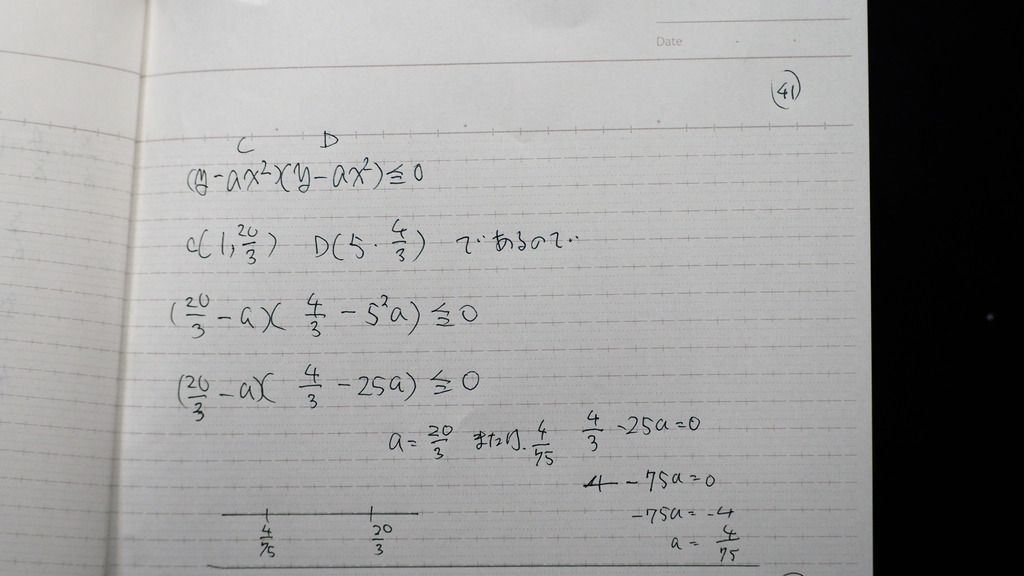
42
求めるのは
aの 整数値であるから
1,2,3,4,5,6

お疲れ様です。
領域を 表す 不等式
01
今回は 領域が
初めに 示されています
この領域を
表す 不等式を 求めなさい
(1)(2)は 兎も角さ
(3)は やばいよね
02
(1)は
Y=xの線を含んで 下側
と
y=0 以上の 領域
であるから
うまく くっつけられて
こんな感じで
03
(2) これはさ
絶対値 の グラフ
04
y=0 と y=|x|
について
y=0以上
y=|x|以下
y=|x|以下は
y-|x|=0以下に 式変形して
ゼロ以下 × ゼロ以上
(マイナス) (プラス)
= ゼロ以下
(マイナス)
で
くっつけてですよ
こんな感じで
05
問題はさ
これなんだけど
境界線を一つ
越すごとに
+、-、+、-と 変わっている
境界線の方程式を
拾ってきて
=0の形にして
全部 掛け合わせてじゃナイスカ
いいんかな
領域の ひとつを 選んできて
その中の 要素を 代入したらば
06
プラスになるんだね
そこで
境界線を 含んでいるので
=もつけて
プラス
これが 答えなんだけど
07
実際に なってるか
計算してみるとさ
08
なんか 物理かなんかの
実験データ みたいな感じだけどさ
09
交互に
+、-、になってるようですが
10
めんどうだから
電卓を たたいてると
11
そういえば
実験とかで
電卓 が 必要になって
けっこう 高いの 買ってたかな
(学生の頃)
12
高校までと違って
試験のときに
電卓 持ち込み可
なんて言う試験も
ざらだし
( ただし
プログラムは 不可とかさ)
13
始めん頃
不思議な感じで
試験してましたが
14
あ コロコロ 使ってますか
電卓が ある時はいいけどさ
て計算の時に
マイナス 何乗
とかさ
マイナスの時は
左へ
今回は 3コロコロ
15
計算自体は
プラスか マイナス で
出てくるけど
境界線を 含んでますため
= も 付けてね
16
学生の時はさ
実験が 長引くと
学食に
行けなくて
17
よくさ
実験中に
召しが食いたい
18
我々は
やらなかったけど
化学かなんかの 人たちで
実験中に
おなかがすいて
ビーカーで ラーメン煮てたとか
むかしは
良くありましたね
教授は 寛大で
やっても いいけど
チャンと 洗っときなさいよ!!
(わたしん時は まだ
インターネットが 始まったばかりで
パソコンも
カセットテープ
フロッピーディスク
が メインで
情報が 遅かった
だから 拡散されず あまり
問題にならず すんでましたが
イマハ
うっかり いたずら半分に
やっちゃうと
社会の 歯車の 一つだと
いうことを 忘れちゃうと
すぐ 大問題に なってしまうので
よく考えてじゃナイスカ)
19
そんなことは
兎も角
今回の ようなケースは
こんな感じに
なるよです
20
では 類題 行ってみましょう
21
大きい円と
小さい円
大きい円の 外側で
カツ
小さい円の 内側
境界線含む
大きい円は 中心が (0,0)半径1
22
小さい円は
中心と 半径が わかんないけど
円周上の 3点が わかってるので
計算してみますと
まず (0,0)
23
(0,1)
(1,0)
24
式が3本出て来て
②③から
n=m
25
➀に n=mを
代入して
半径がさ
半径は 長さ であるんで
正の値
26
nと m を
全部 mにして
そうするとさ
rの二乗もさ
で
m=1/2
27
n、m 、rが出てきたので
方程式が出来上がって
28
その 周上 および 内部
大きい円と 合わせると
こんな感じで
29
これはさ
円と 絶対値の グラフ
2本の線分と 円で 囲まれた
境界線上と 内部
30
絶対値をさ
外すと
マイナスの時は
絶対値 ヲ 外すと 前に
マイナスが
ところが
絶対値を 外したときに
xが プラスになってるので
絶対値の前に マイナスをつけて
31
こんな感じで
32
円の方は 問題なく
であるので
こんな感じに
33
次がさ
これは
今回は 逐次 調べないけど
境界線を
一つ 越えると +、-、+、
と変わってるので
境界の方程式を
拾ってきて
34
=0に 変形して
掛け合わせて
領域になってる
エリアの 点を代入して
マイナスになったので
境界線も 含むから
=もつけて
こんな感じに
35
問題を 読んでいただいて
36
三角形を
直線の 方程式で
囲んで 行く時に
直線の 方程式は
こんなでしたね
この3番目を 使って
37
こんな感じじゃナイスカ
38
C、D、ッテいう点は
ここ と ここ
39
座標が 出てきたので
40
二次関数の グラフは
こんな感じなので
Cのときより 下
Dの時より 上
マイナス プラス かけて
マイナスになる
41
この不等式を
解くと
42
求めるのは
aの 整数値であるから
1,2,3,4,5,6
お疲れ様です。
2023年03月28日
08031 大人のさび落とし 図形と方程式 領域(2)
図形と方程式 大人のさび落とし
01
次の ような 不等式の 領域を
図示せよ
直線 y=mx+2が 2点
A(3,2) B(-1、4)
を 結ぶ線分と 交わるときの
mの範囲を 求めよ

02
可能性としてじゃナイスカ
プラス・マイナス
マイナス・プラス
であるから
まず 大きく 2つに場合分け

03
集合M と 集合N とするでしょ
Mの中の➀②
Nの中の③④
の 共通領域 を
合わせたものが
求める 領域になるので
➀キャップ②:M
③キャップ④:N
M カップ N
(➀キャップ②) カップ (③キャップ④)

04
集合Mの ②の方は
円の方程式で
中心が 原点 半径 1の
周上 および 内部
➀の方は
絶対値があるので
絶対値を プラスで 外すとき
絶対値を マイナスで 外すとき

05
プラスで 外すとき
マイナスで 外すとき
絶対値の 中味の Aを
挟む かたちにして
Aの 符号を
正にすると
なるでしょ

06
であるから
集合Mの方の
共通領域は
これらの 共通部分

07
ここです
円の 内部と
直線の 下と 上
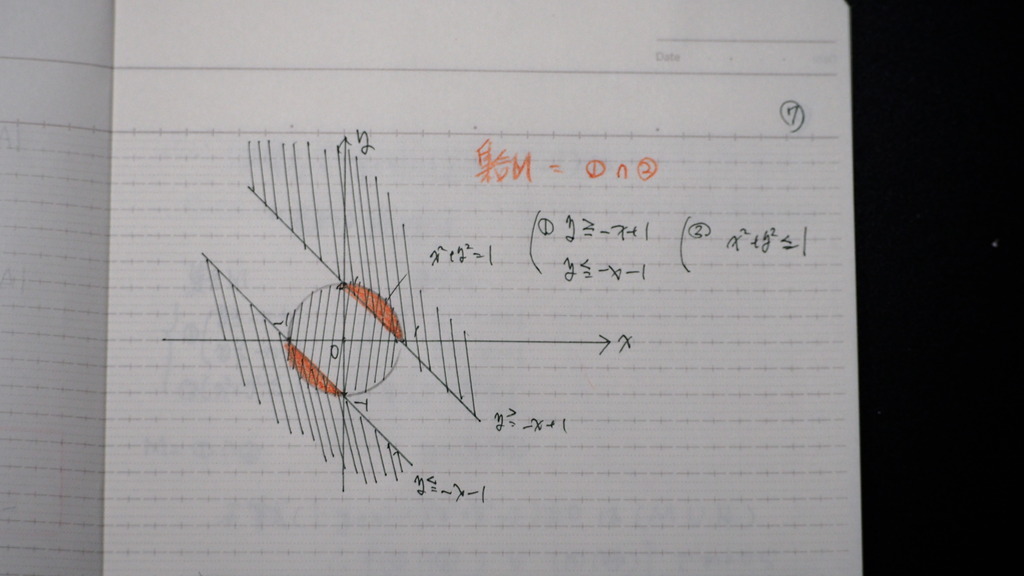
08
集合Nの方は
絶対値は
こんな感じで
こんどは円の外側

09
であるから
まとめると
与式は
二つの 可能性に 場合分けで来て
その M と N の 集合を
合わせたものが
領域になるから

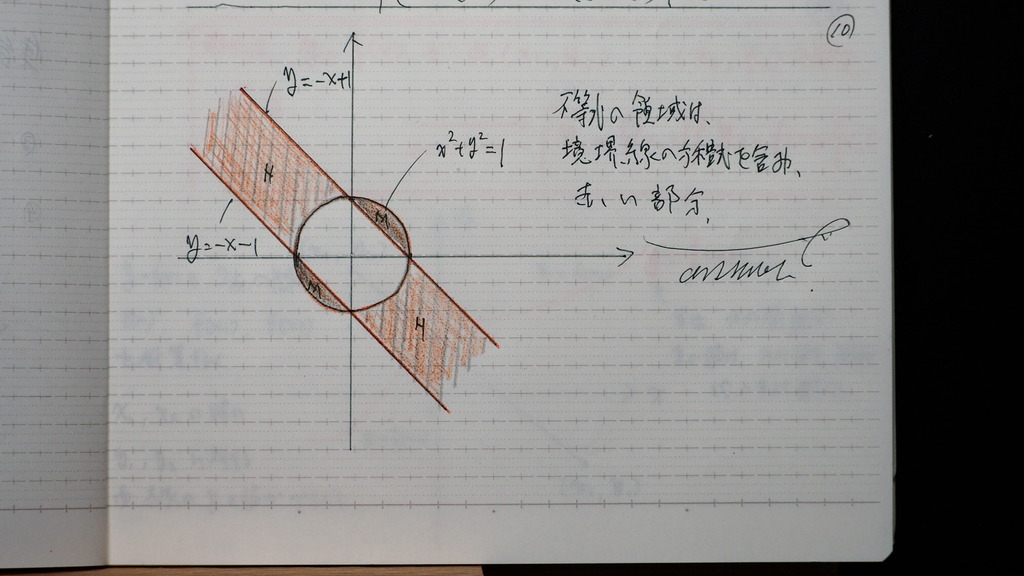
10
こんな 形で
境界線を 含み 赤い所
堺 の 字が
間違ってました
こっち 界
11
かっこ 2は
直線が 線分と 交わると
その時に
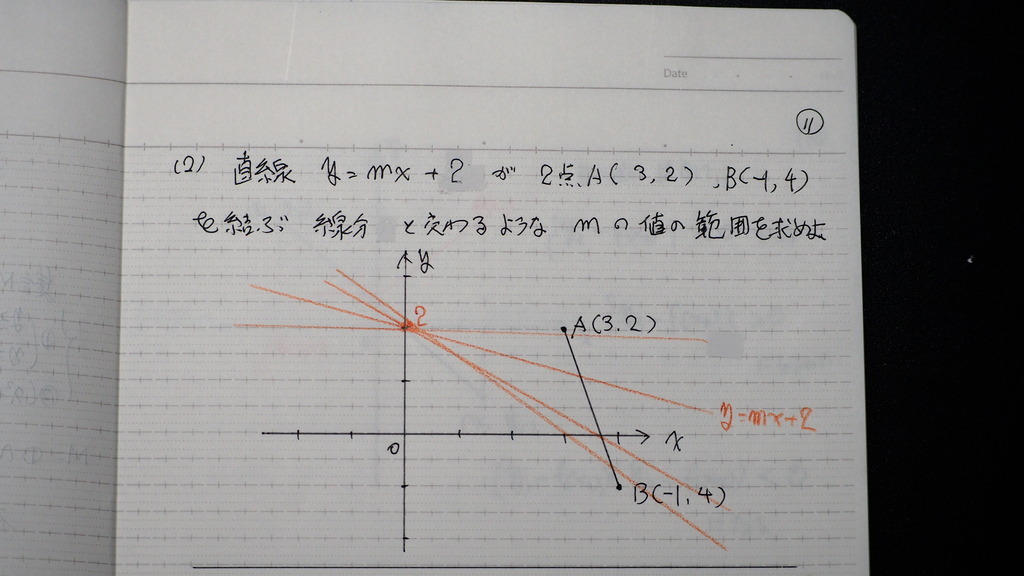
12
曲線が 線分を 突っ切てると
線分の 両端の 座標
の x と y の yは
曲線上の xに 対応する
曲線上のy つまり f(x)
と 大きさを
比べると
y1-f(x1)
y2-f(x2)
一方の端が プラスならば
他方の端は マイナス
であるから
曲線 直線が 線分と 交わる領域は
この二つの 積が
マイナス か 等しい所
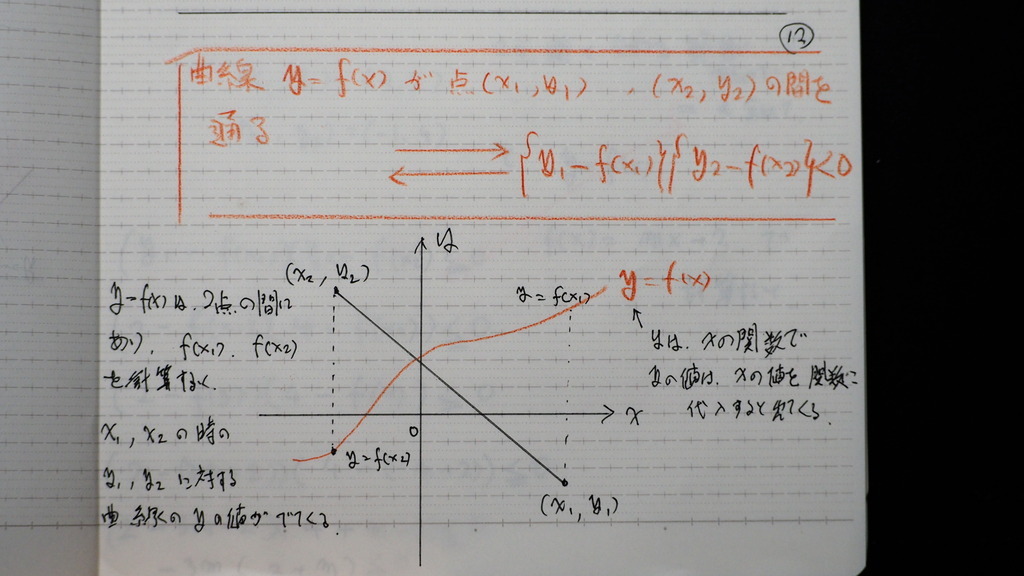
13
こんな感じに表現できるので
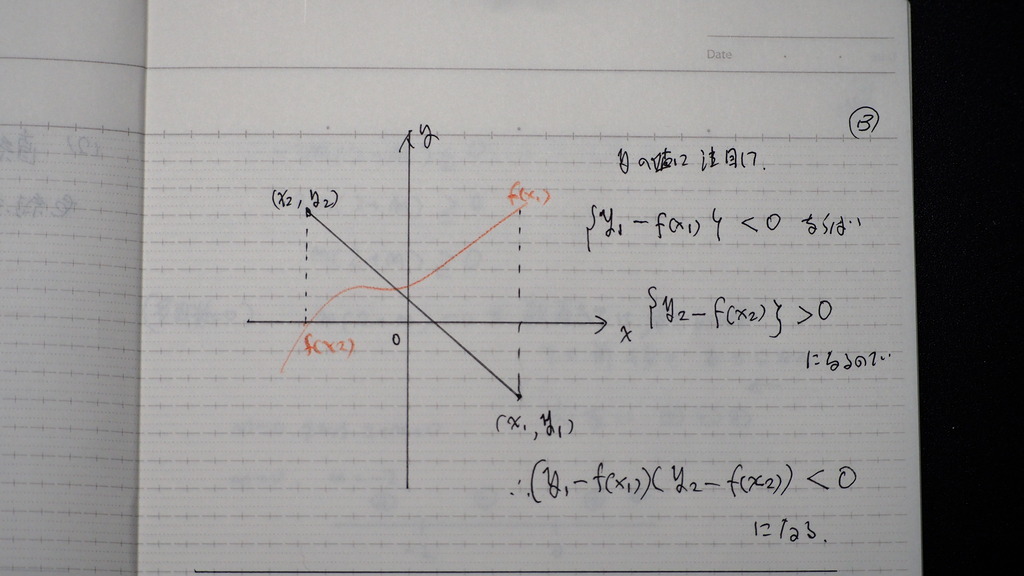
14
これを 計算するじゃナイスカ

15
不等式が
わかんなくなった時は
各因数が ゼロ になるとこを
数直線に 書き込んで
その前後を
交互に
左 ← 右
右から左に
+ - +

16
不等式が
ゼロ 以上になってるとこは
ここ
これが m の 値の範囲
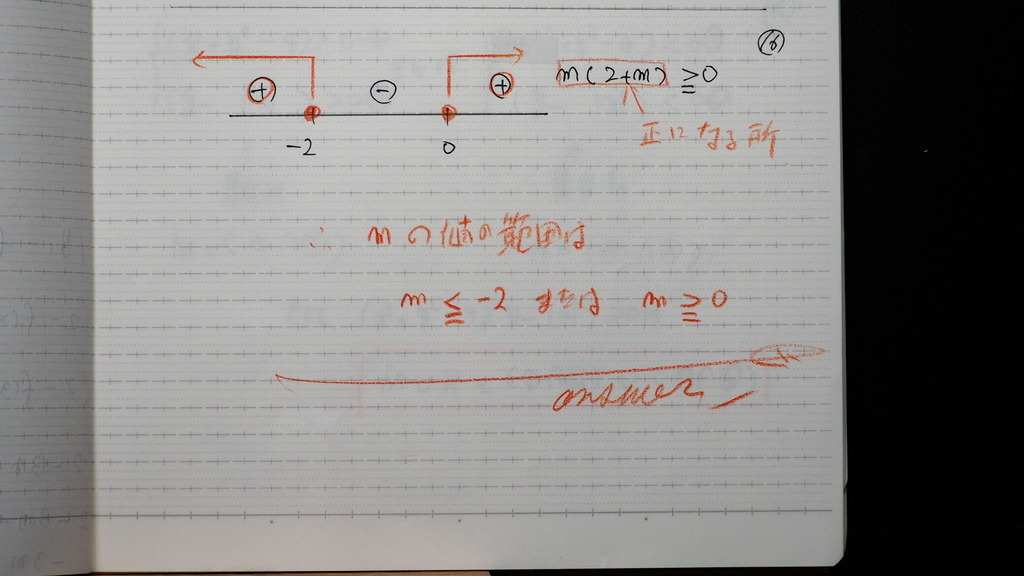
17
では 類題行ってみましょう

18
場合分け
それぞれの 共通領域を
合わせたものが
求める 領域

19
集合Mの方は
円の 方程式は
円の外側

20
絶対値は
こんな感じに なるので
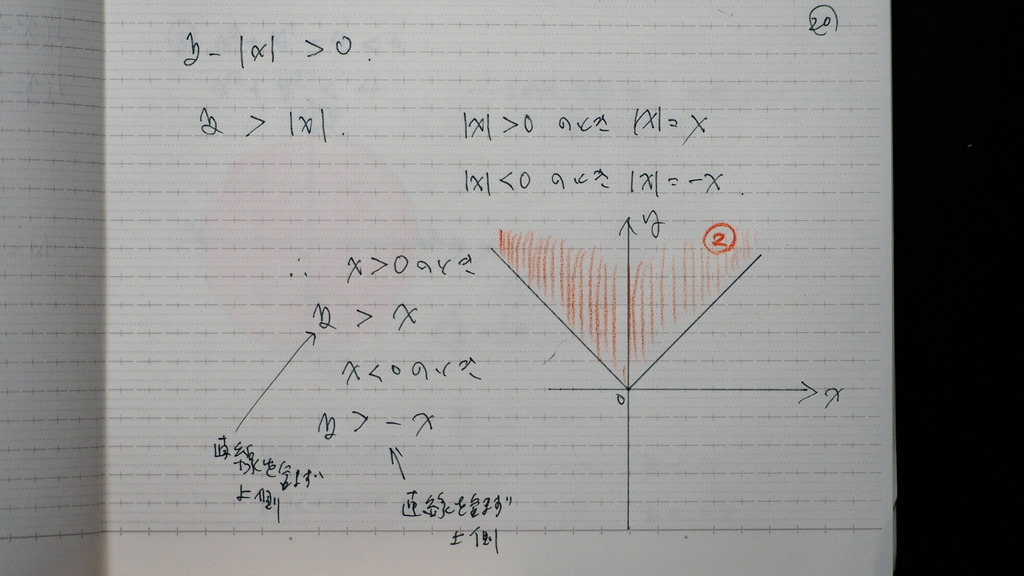
21
場合分け 集合Mは
ここ 赤い所
境界線含まず
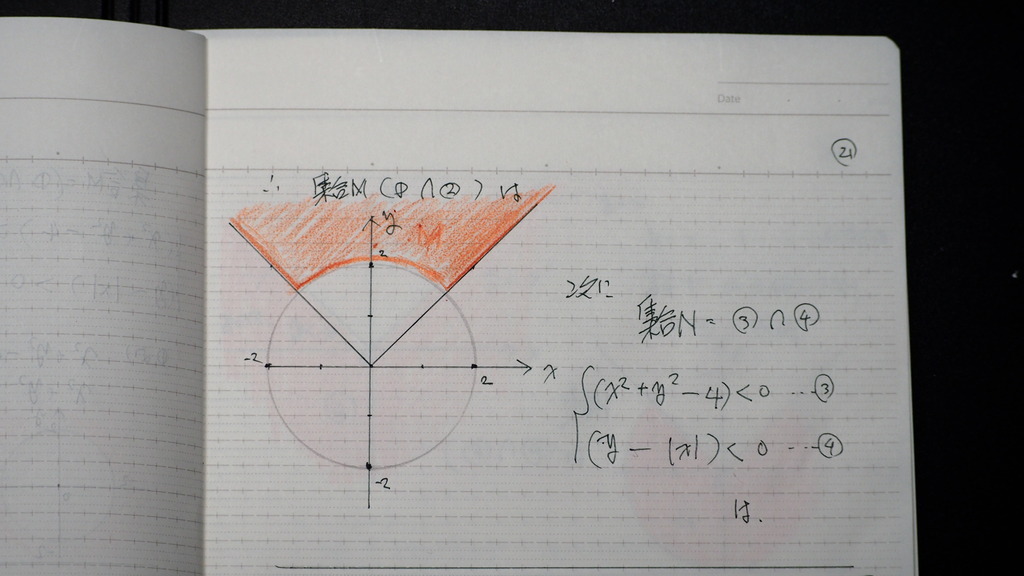
22
集合Nは
円の内部と

23
こんな感じなので
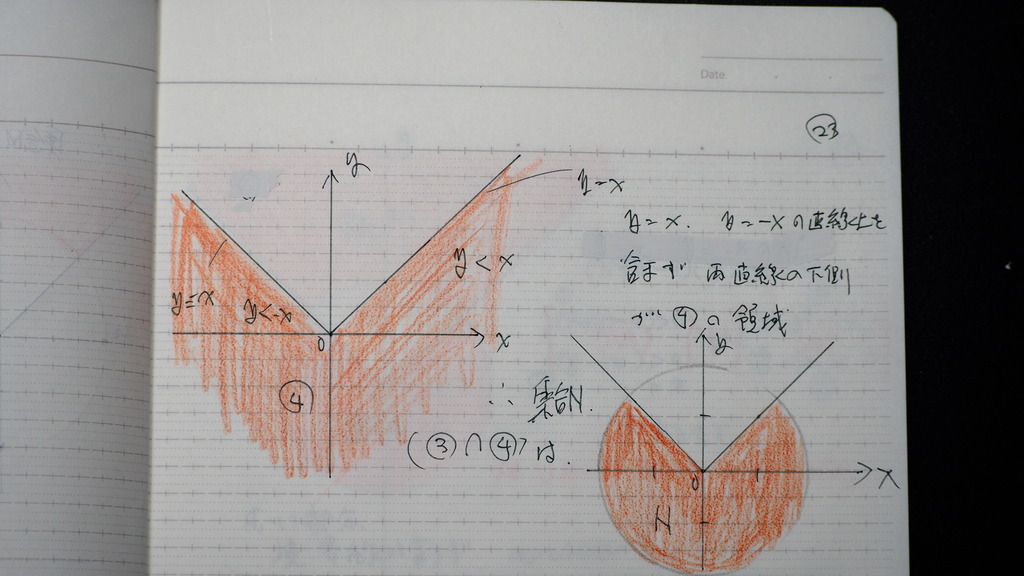
24
まとめると
与式は
大きく 2つに 場合分けで来て
それぞれの 共通部分を
合わせると
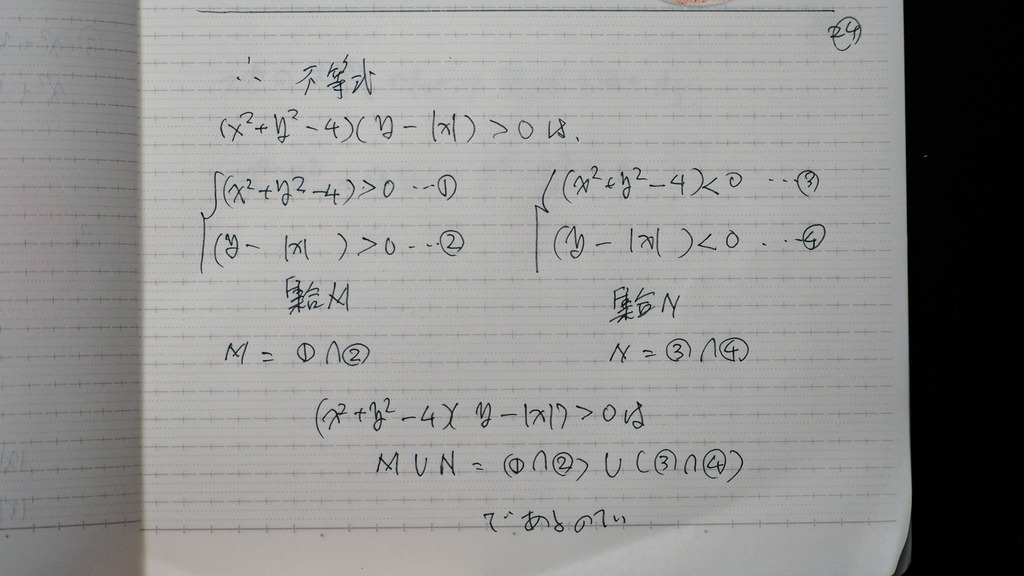
25
こんな感じに
なるですよ
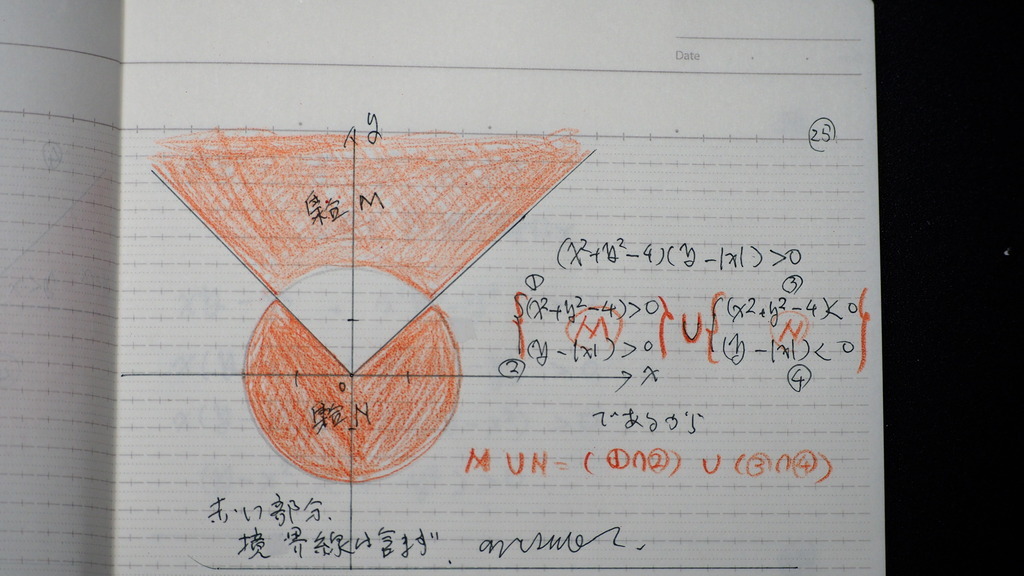
26
次の
不等式のあらわす
領域を 図示せよ

27
先ず 因数分解
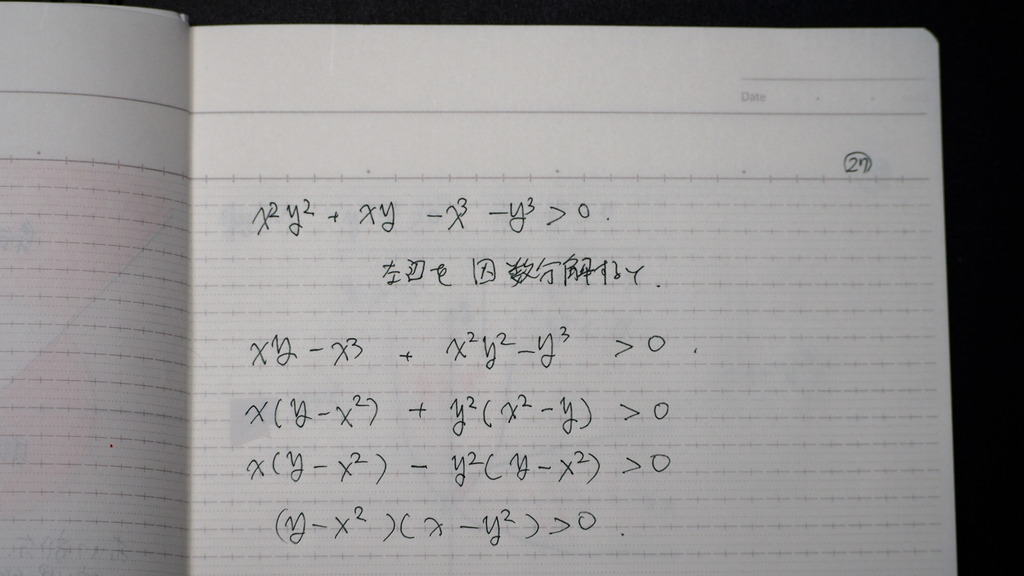
28
因数分解が できれば
場合分け
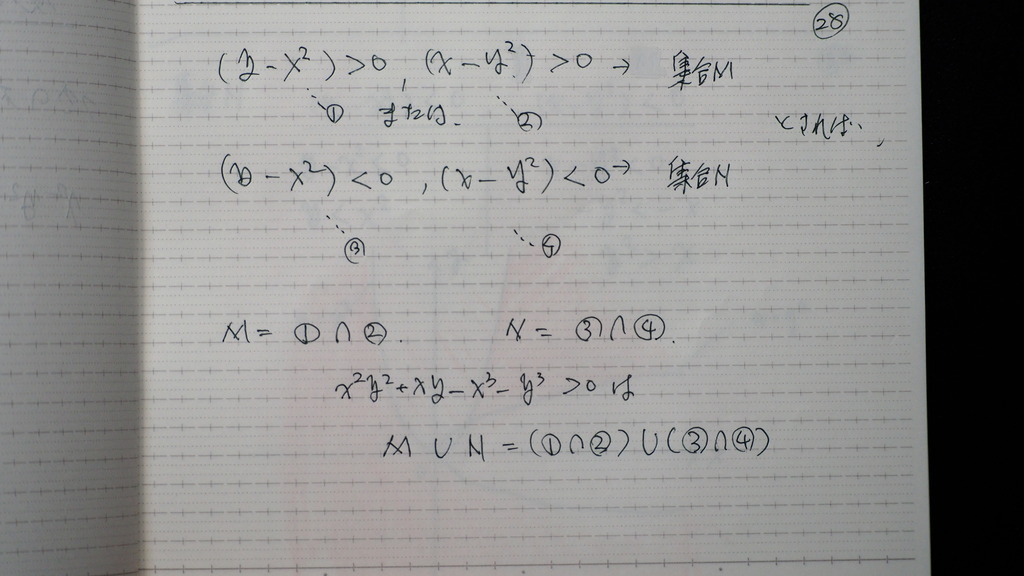
29
集合 ん~
大丈夫かな
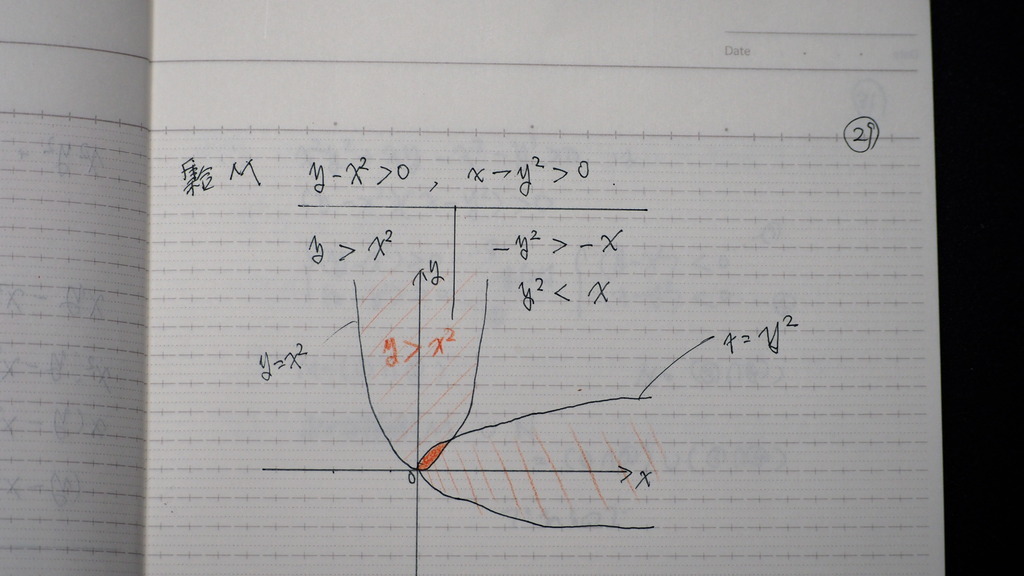
30
こう言うさー
問題なんだけどさ
いま やってるんはさ
すうがくだ~からさ
え わかってる
それなら い いんだけどさ
ホントに 大丈夫かな
だから なんなんだ
赤い所
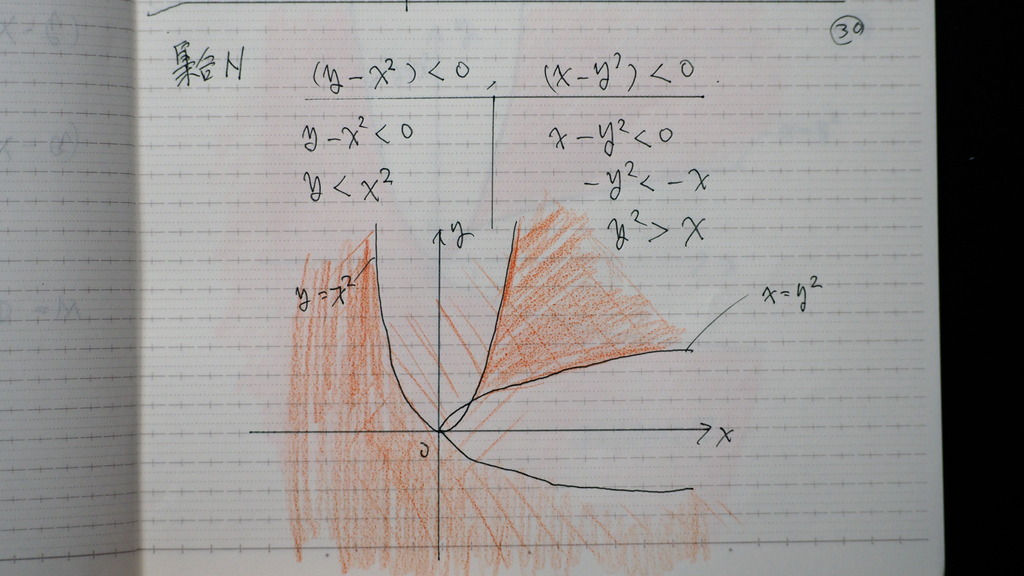
31
だから
まとめると
なので

32
これだ
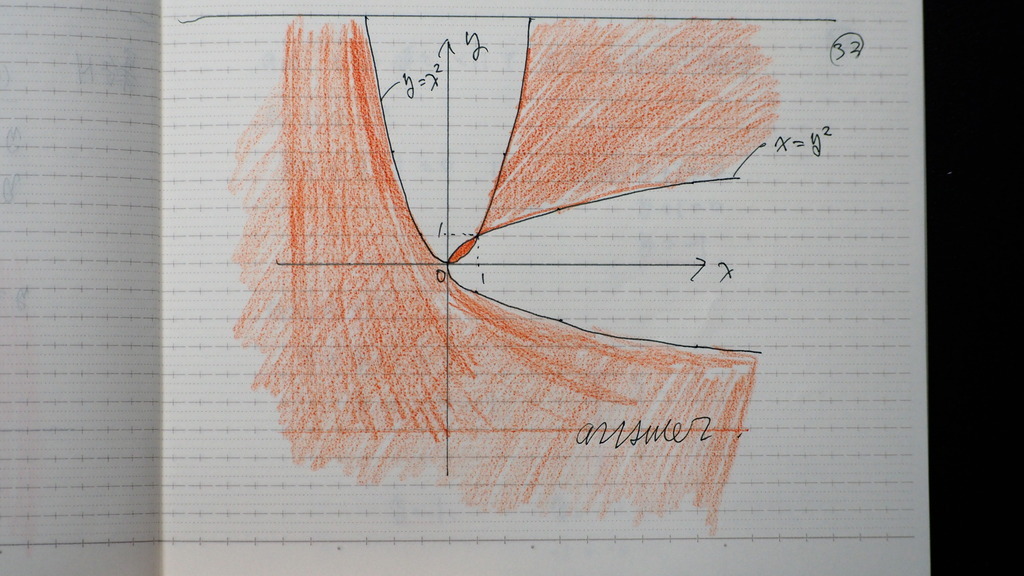
33
ぐわいわり
えーと
問題
読んでいただいて

34
定点の座標から
どんな 値でも いいって言ってるから
都合のいいとこを
2っつ 持ってきて

35
コレダ
で
与式を 変形と言うか
f(x)= に替えてじゃナイスカ
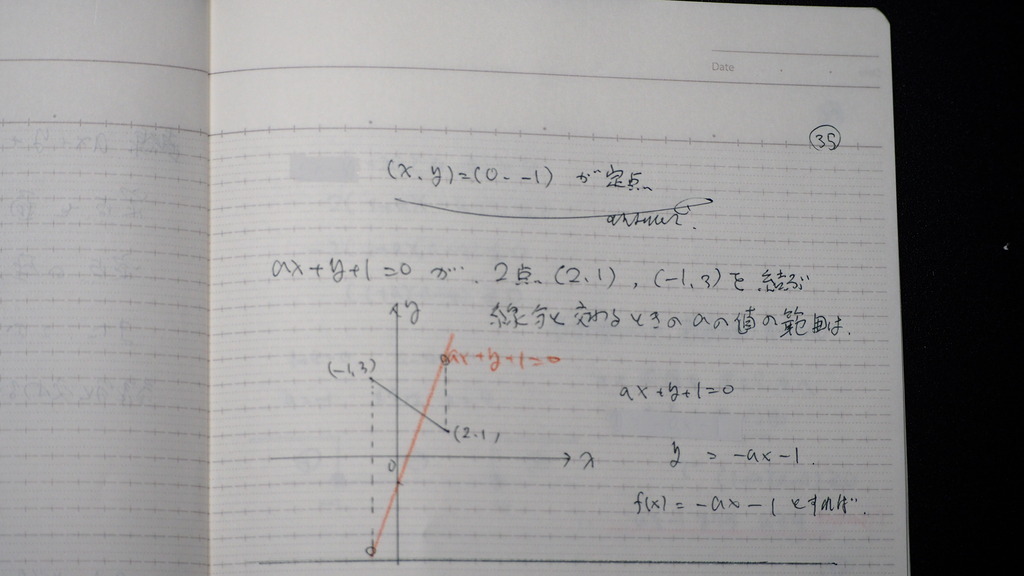
36
直線が 線分と交わるときの
領域の 求め方で

37
これを 解けば

38
最後は
2点が 在って
一方が 円の 内側
他方が 円の 外側
になる
円の 中心座標の 領域を
求めよ
円の 方程式は これなんだって
そこで

39
f(x、y)= にすれば
で
2点を代入したものが
領域の 外と 内 なので
積が マイナス
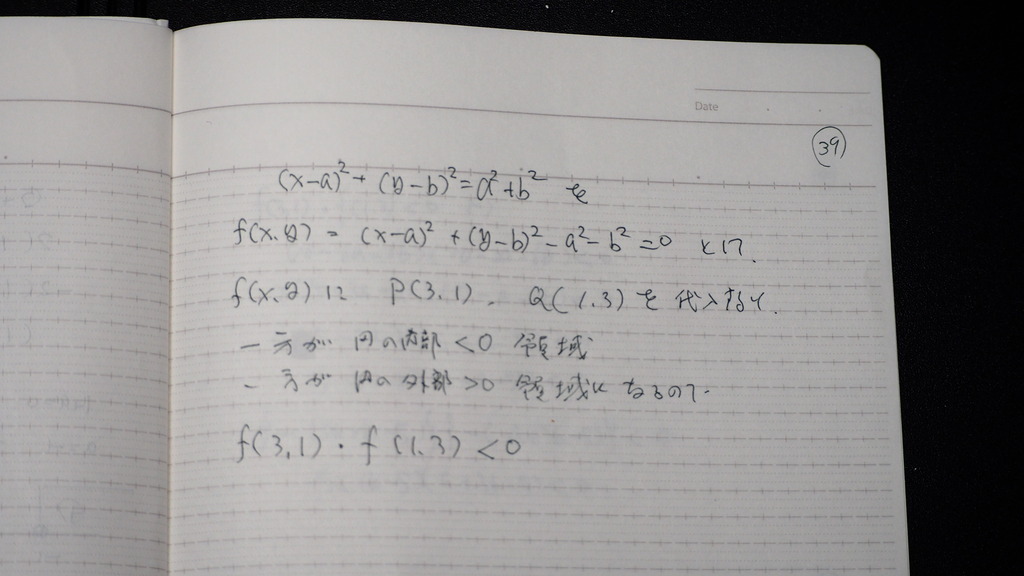
40
これを 計算すると
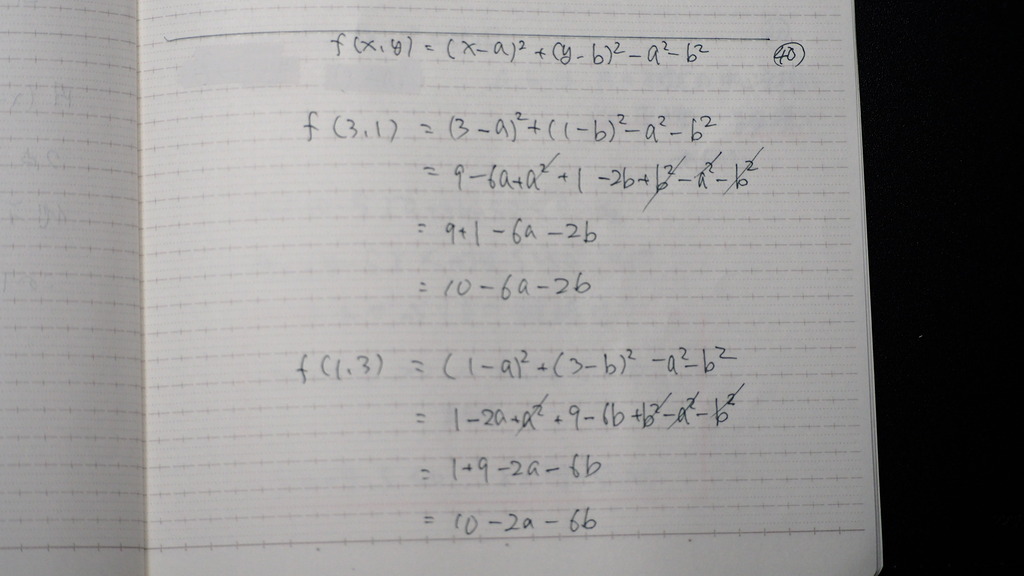
41
二つの 積が マイナス
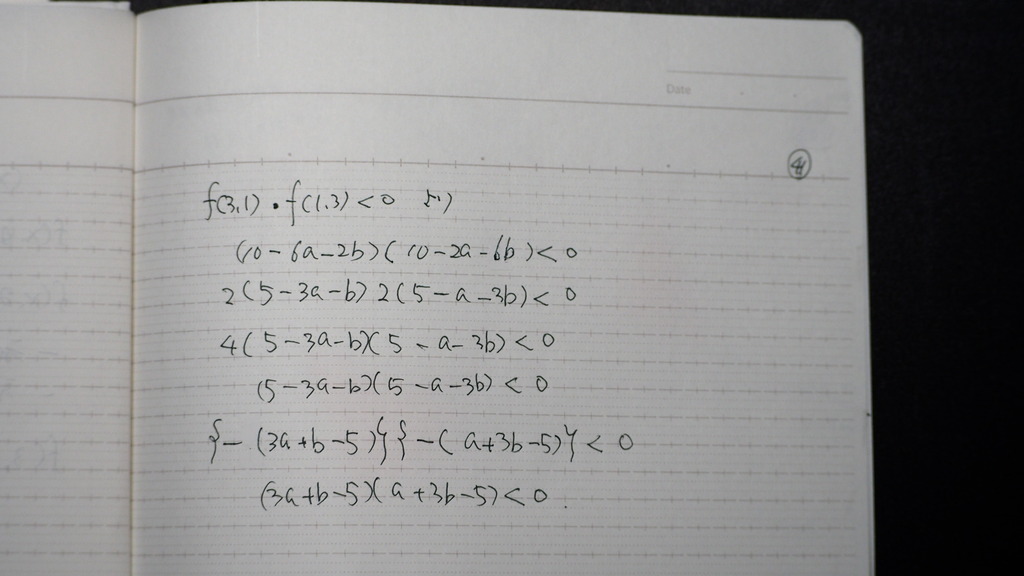
42
ところで
ここでいうところの
a,bは
それぞれ
円の 中心の
x座標 y座標
であるので
x、y を a,bに 代入して
今までのように
領域を
場合分けして
求めると

43
それぞれ
こんなだから
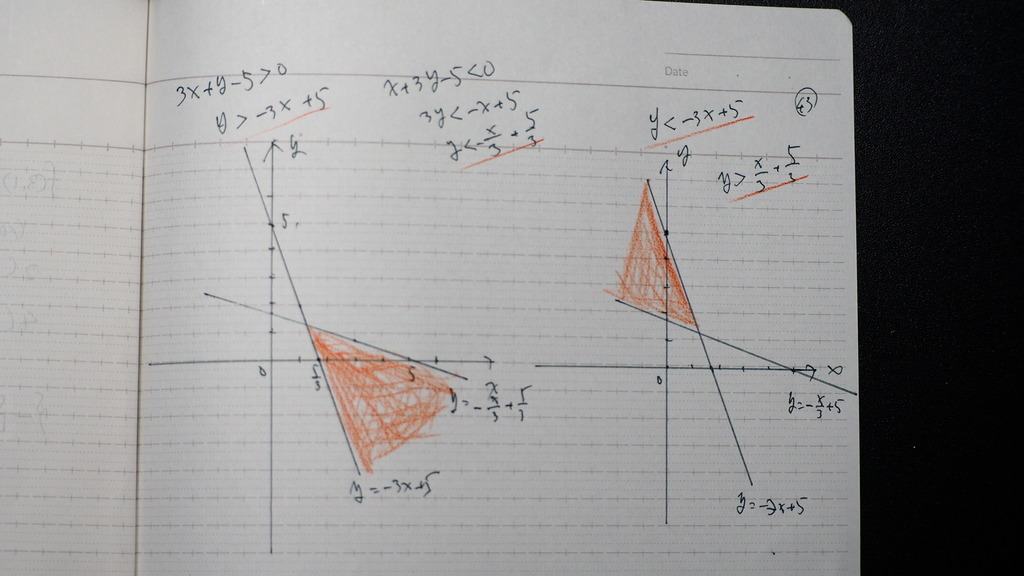
44
こんな感じに なるんだって

お疲れ様です。
01
次の ような 不等式の 領域を
図示せよ
直線 y=mx+2が 2点
A(3,2) B(-1、4)
を 結ぶ線分と 交わるときの
mの範囲を 求めよ
02
可能性としてじゃナイスカ
プラス・マイナス
マイナス・プラス
であるから
まず 大きく 2つに場合分け
03
集合M と 集合N とするでしょ
Mの中の➀②
Nの中の③④
の 共通領域 を
合わせたものが
求める 領域になるので
➀キャップ②:M
③キャップ④:N
M カップ N
(➀キャップ②) カップ (③キャップ④)
04
集合Mの ②の方は
円の方程式で
中心が 原点 半径 1の
周上 および 内部
➀の方は
絶対値があるので
絶対値を プラスで 外すとき
絶対値を マイナスで 外すとき
05
プラスで 外すとき
マイナスで 外すとき
絶対値の 中味の Aを
挟む かたちにして
Aの 符号を
正にすると
なるでしょ
06
であるから
集合Mの方の
共通領域は
これらの 共通部分
07
ここです
円の 内部と
直線の 下と 上
08
集合Nの方は
絶対値は
こんな感じで
こんどは円の外側
09
であるから
まとめると
与式は
二つの 可能性に 場合分けで来て
その M と N の 集合を
合わせたものが
領域になるから
10
こんな 形で
境界線を 含み 赤い所
堺 の 字が
間違ってました
こっち 界
11
かっこ 2は
直線が 線分と 交わると
その時に
12
曲線が 線分を 突っ切てると
線分の 両端の 座標
の x と y の yは
曲線上の xに 対応する
曲線上のy つまり f(x)
と 大きさを
比べると
y1-f(x1)
y2-f(x2)
一方の端が プラスならば
他方の端は マイナス
であるから
曲線 直線が 線分と 交わる領域は
この二つの 積が
マイナス か 等しい所
13
こんな感じに表現できるので
14
これを 計算するじゃナイスカ
15
不等式が
わかんなくなった時は
各因数が ゼロ になるとこを
数直線に 書き込んで
その前後を
交互に
左 ← 右
右から左に
+ - +
16
不等式が
ゼロ 以上になってるとこは
ここ
これが m の 値の範囲
17
では 類題行ってみましょう
18
場合分け
それぞれの 共通領域を
合わせたものが
求める 領域
19
集合Mの方は
円の 方程式は
円の外側
20
絶対値は
こんな感じに なるので
21
場合分け 集合Mは
ここ 赤い所
境界線含まず
22
集合Nは
円の内部と
23
こんな感じなので
24
まとめると
与式は
大きく 2つに 場合分けで来て
それぞれの 共通部分を
合わせると
25
こんな感じに
なるですよ
26
次の
不等式のあらわす
領域を 図示せよ
27
先ず 因数分解
28
因数分解が できれば
場合分け
29
集合 ん~
大丈夫かな
30
こう言うさー
問題なんだけどさ
いま やってるんはさ
すうがくだ~からさ
え わかってる
それなら い いんだけどさ
ホントに 大丈夫かな
だから なんなんだ
赤い所
31
だから
まとめると
なので
32
これだ
33
ぐわいわり
えーと
問題
読んでいただいて
34
定点の座標から
どんな 値でも いいって言ってるから
都合のいいとこを
2っつ 持ってきて
35
コレダ
で
与式を 変形と言うか
f(x)= に替えてじゃナイスカ
36
直線が 線分と交わるときの
領域の 求め方で
37
これを 解けば
38
最後は
2点が 在って
一方が 円の 内側
他方が 円の 外側
になる
円の 中心座標の 領域を
求めよ
円の 方程式は これなんだって
そこで
39
f(x、y)= にすれば
で
2点を代入したものが
領域の 外と 内 なので
積が マイナス
40
これを 計算すると
41
二つの 積が マイナス
42
ところで
ここでいうところの
a,bは
それぞれ
円の 中心の
x座標 y座標
であるので
x、y を a,bに 代入して
今までのように
領域を
場合分けして
求めると
43
それぞれ
こんなだから
44
こんな感じに なるんだって
お疲れ様です。
2023年03月23日
大人のさび落とし08030 図形と方程式 (領域)
08030 図形と方程式 ( 領域 )
01
集合を 表すときの
数学的な 書き方ですが
A B と言う 2つの
集合があるときに
包含関係を 調べよ
02
円の方程式の時の
不等式が 表す領域は
こんなだったですので
集合Aは
こんな感じ
03
集合Bは
絶対値付の 1次不等式
左辺に Y 右辺に X の
ある形にして
Yについて
絶対値を 外すと
04
右辺の マイナスつき 絶対値Xを
外すと
05
表にしたらば
こんな感じの 場合分けになって
じゃナイスカ
06
➀②③④のグラフを
書いてみると
領域は
線上を 含まず
どれも 線分の 下側
絶対値によって
変域に 制限がかかってるので
グラフにすると
07
➀は
ここ
08
②は
ここ
09
③は
Y の前に マイナスがあったので
払ったら
向きが変わって
線分を含まず
上側
10
④
Yの前に マイナスがあったので
払って
符号の 向きが変わり
線分を 含まず
上側
9-2
これを まとめると
こんな感じの 周を含まない
正方形領域になって
10-2
A と B の 包含関係は
BはAに 含まれる
11
領域の判定方法は
一般に
曲線で
平面が 分断されているとき
在る点に対して
不等式が 成り立てば その点は 領域にある
不等式が 成り立たなければ その点は 領域にない
12
つぎの 不等式の 表す領域を
図示せよ
13
不等式の 問題では
要注意もんだい
はじめて やるときや
忘れてると
ひっかかっちゃう
14
グラフを書くときの
癖と言うか
習慣と言うか
グラフを書いたら
かっこ 1は xy=1 じゃなくて
y=1/x の グラフの
不等式であるから
今回は 式変形上は
おなじだけど
領域の時は
違うんですよ
15
6っの 点を 選んで
調べてみると
赤い所になる
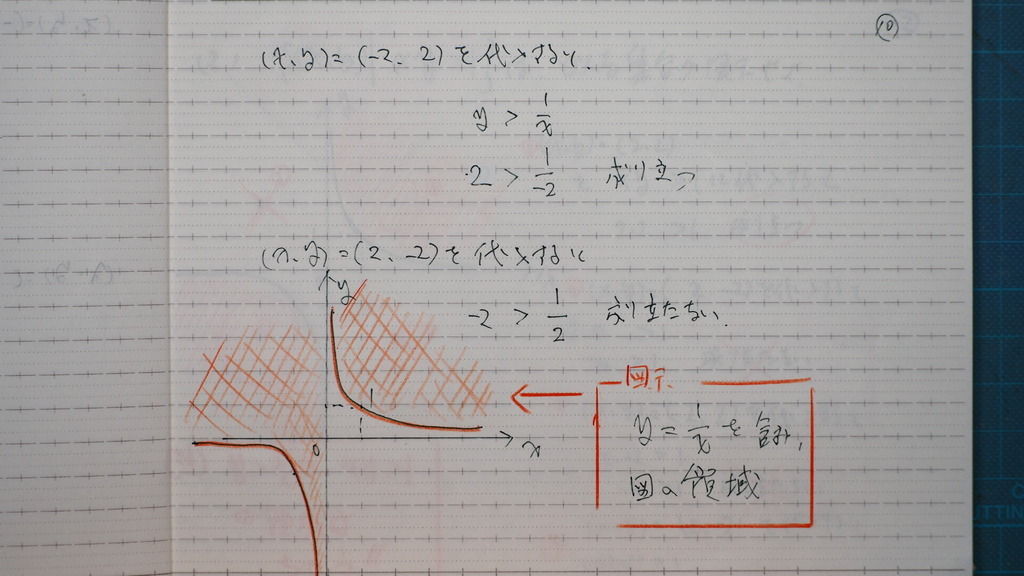
16
これを xy=1の
不等式で
調べると
ほら
ほら
違うじゃん
ねー
17
であるから
正しい方の 領域と
y=x の 下側
を みると
境界線は 含まず
赤い所
18
次の 不等式の 領域を
求めよ
19
絶対値を
0以上で
外すと
20
円の方程式 周上と内部
それと
絶対値を 外したときの
条件から
21
絶対値を
負で 外すと
22
今度は
円の方程式が ちょっと変わって
周上と内部
絶対値を 外した 条件を
入れると
23
小さい円と 大きい円
ピッタリ くっついてると思うけど
計算して
見るとさ
24
大きい円と 直線の 交点は
25
これだ
26
小さい円と 直線の交点は
コレダ
あってる
27
だから
こんな ヒョウタンみたいな かたちに
28
次の 点A 、B について
次のPの集合は
どうなるか
29
P(x,y) として
AP BP
点と直線の距離を
計算したらば
30
ソレゾレ
こんなだからさ
31
両方とも
線分の 長さで
正の 数量だから
二乗しても
大小関係は 変わらない
そこで
辺々 二乗 して
√を はずして
32
円の 方程式かなとも思ったんだけど
整理したらば
簡単な1次式になって
こうです
33
今の要領で
B も見ていくと
34
点と直線の距離から
辺々二乗して
展開して
35
まとめて
見ると
円の方程式になって
36
こんな感じ
37
次はですね
領域の 面積を
求めるんですが
38
A,B,C
領域があって
AカップB と ( A ∪ B ) キャップ C
であるから
Aと Bの 全てに対して
Cが 共通している部分
39
Aの 領域がさ
絶対値が 2重になってる
歌の グループの さ あれはいいんだけど
いいじゃナイスカね
絶対値の時は
深呼吸して
えーと
40
先ず外側から
そうするとさ
-2以上 2以下
または
-2以下 と 2以上
41
さらに
その 内側の 絶対値 xは
0以上と 0以下で
符号が変わるので
今回の領域は 線上を含みますため
等号が 正の符号にも
負の符号にも 付いてます
42
場合分けを して
はずしてくと
➀ Xが
-2以下の時
43
②
Xが -2以上 0以下の時
44
③
Xが 0以上 2以下の時
45
④
Xが 2以上の時
46
全部 まとめると
Aは
Wみたいな 感じで
Bは 円形で
47
合体
さらに
Cは Yが 2以下
であるので
48
線引きをして
求める
面積は
半円と 台形
を 足した形
パイアール二乗 の 半分と
(上底+下底) × 高さ 割る 2
49
次はね
A,B,C
3つの集合があってですよ
(1) Aが Bに 含まれる
か等しい
50
円の方程式
中心が 原点で 半径が 1
の Aと
放物線 X二乗 +k の 線上を 含
開いた 内側
の B
51
超 拡大図 にするとさ
k=-1 の時は
放物線が
円に 食い込んじゃう
だから
kの値を
放物線が
円に 接するとこまで
下してくると
そこで
判別式
52
X二乗を 消去して
Y の 2次方程式
ここで
判別式:Dを
使て
D=0で
53
判別式から
54
kは -5/4以下
55
(2)は
円の方程式の 周上及び内部
と
直線の線上及び 上側
が
空集合 になるときの k
56
直線が
円に 接するときは
連立から
判別式=0
57
kは プラスマイナス √2
58
であるから
Aと Bの 交わりが
空集合になるためには
kが √2より 大きければよい
お疲れ様です。
2023年01月19日
大人のさび落とし 08029 図形と方程式 不等式と領域
大人のさび落とし
図形と方程式
不等式と領域 (1)
01
どんな感じかと言うと
不等式で示された
領域が
グラフの 上 か 下 か
その見つけ方
y大なりは グラフに上
y小なりは グラフの下
わからないときは
特定の点を 式に代入して
不等式の 向きを 確認する

02
例えば
これらは
こんな場合は

03
こんな 表現で
聞かれるときも

04
キャップは 交わり
カップは 全て

05
動点の時は

06
以上踏まえまして
問題
(1) (2) の
不等式の 示す 領域を
図示せよ

07
(ア)
1次不等式
2次元の直線
3は y切片
傾きが -2
で
グラフの 境界を含み 下側

08
大丈夫かどうか
特定の点を
代入したらば
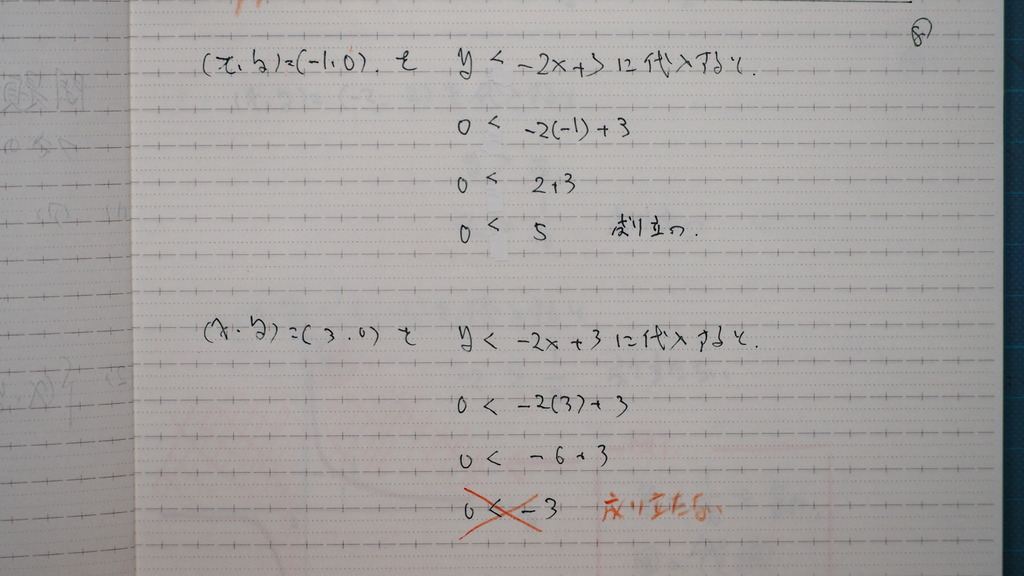
09
グラフは
こんな感じ
式変形する前の
不等式に
特定の点を代入して
調べると
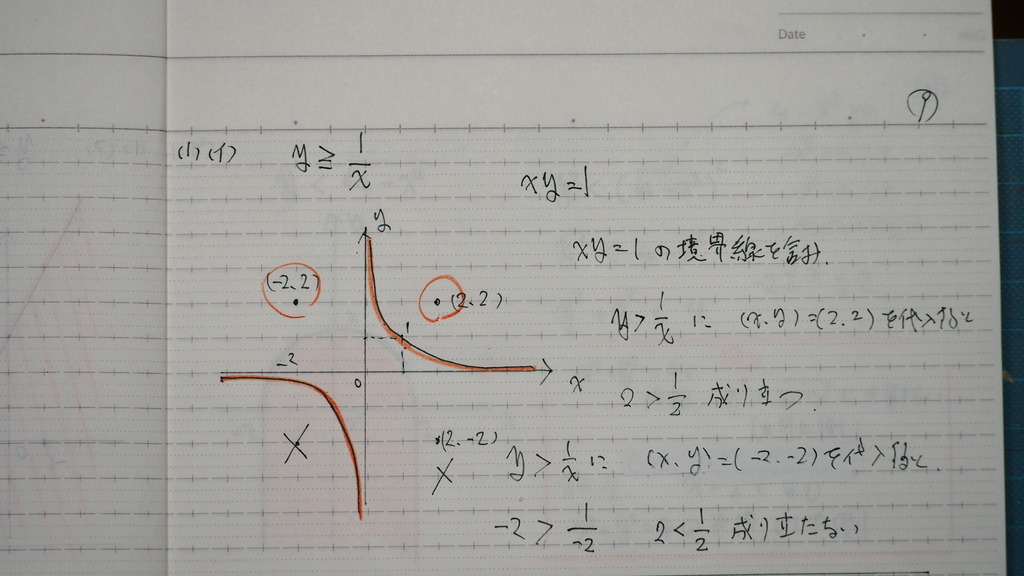
10
こんなかんじ
11
√のとこは
半円
半円より 下側で
-2から 2までの間
注意点は
x=-2 x=2は
境界線含む

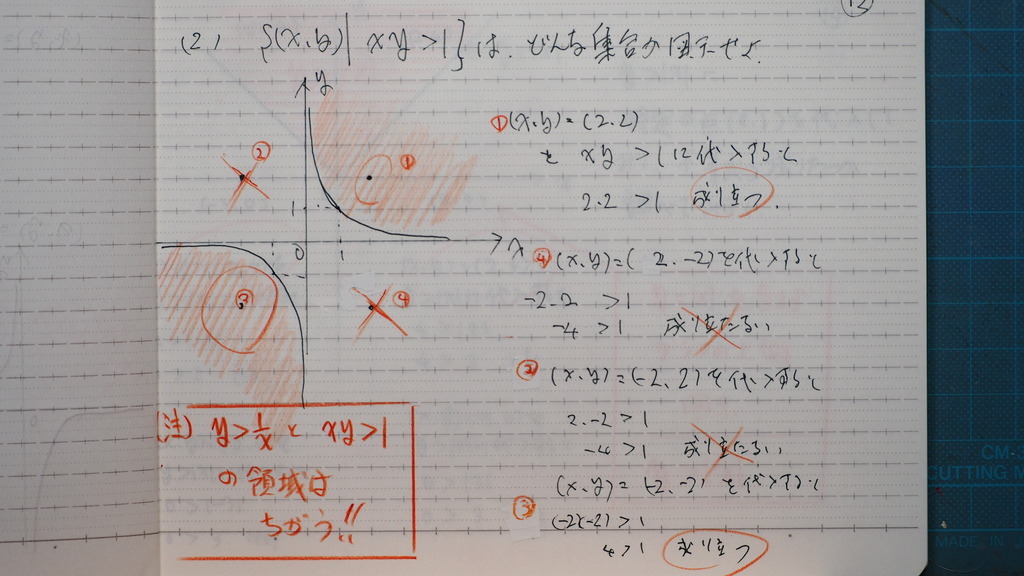
12
さっきの 2番目
(イ)の問題と
おなじでは ないです
13
類題 行ってみましょう

14
グラフを 書いて
点を代入して
確認すると

15
( 画像 未 修正必要 )
場合分けして

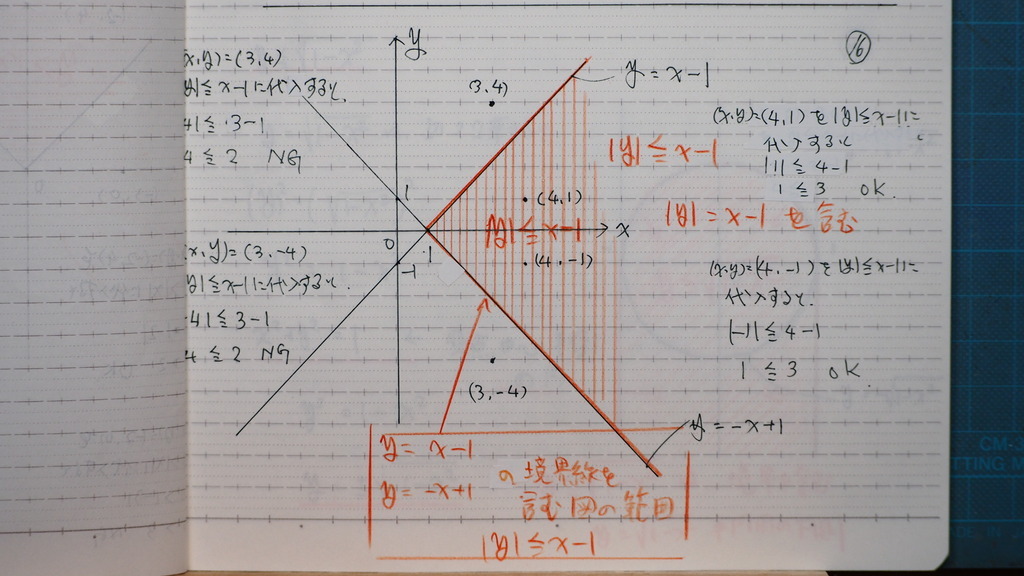
16
グラフの 境界線を含み
この範囲
17
実数条件を調べて

18
半円の 周を含み 下側

19
問題

20
A.N.S
アフタ ・ n ・ショー
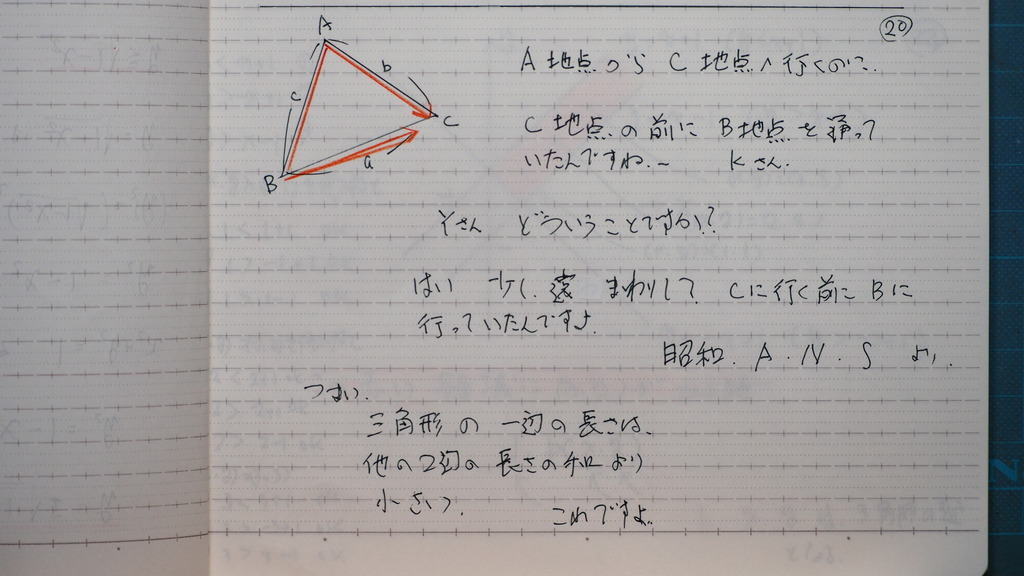
21
三つ 式ができて来て
グラフを
書くじゃナイスカ
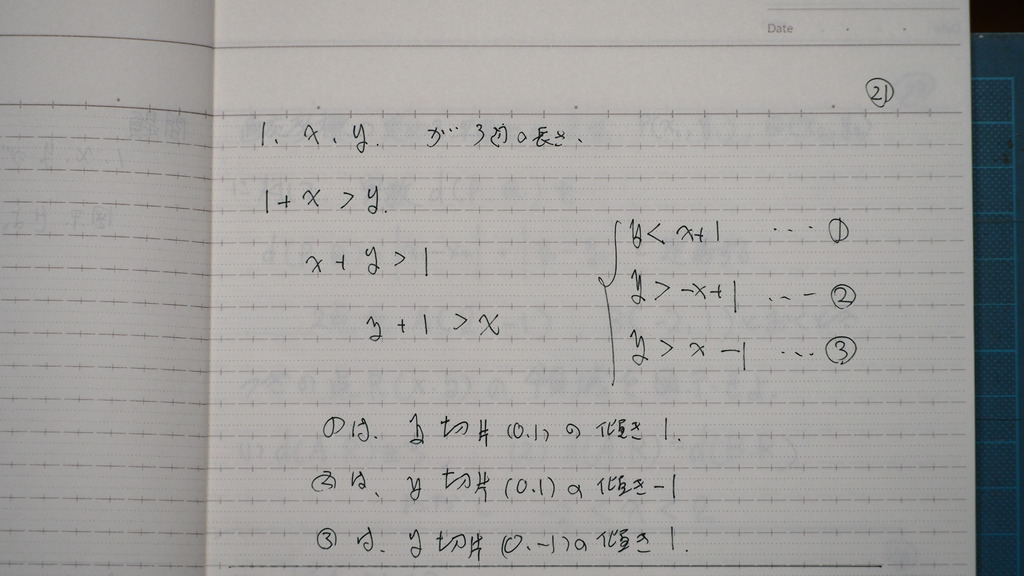
22
この
赤い 領域に 在れば オッケイ

23
問題
これはさ
場合分けが 大変そうだね

24
x系の 絶対値を外すと
2通り
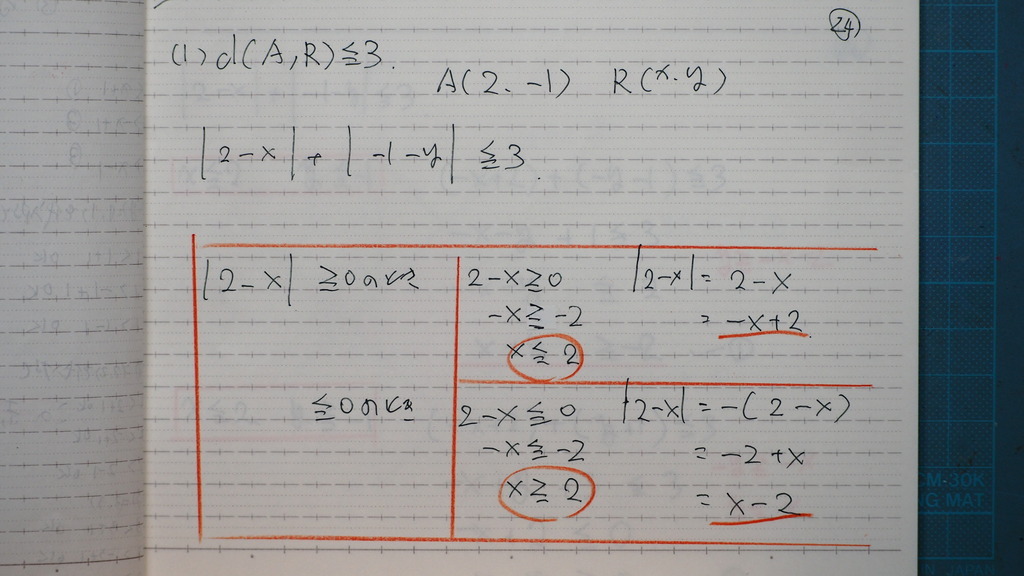
25
y系の絶対値を 外すと
2通り

26
4組に 場合を分けて
まず 2組

27
もう2組

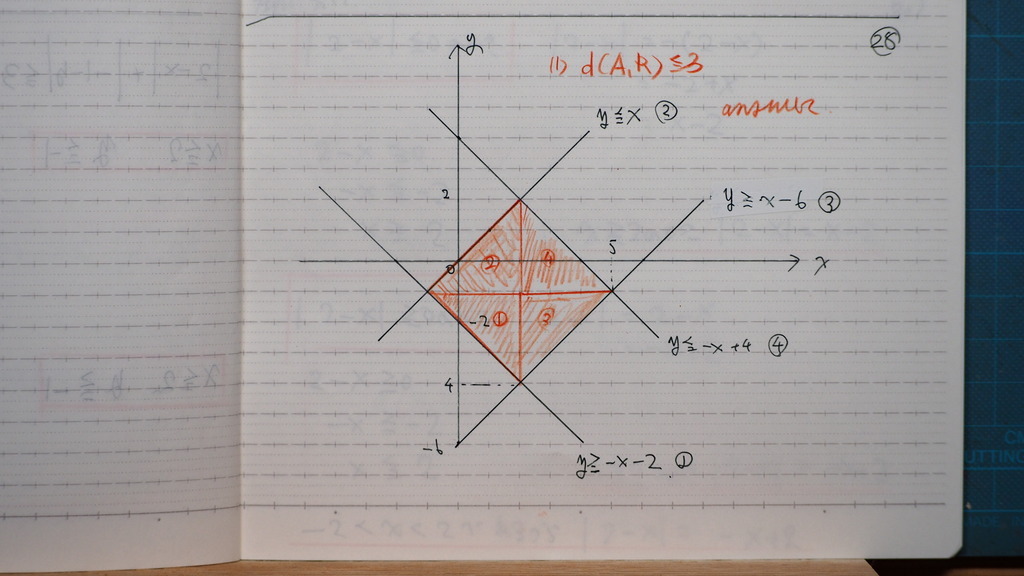
28
それぞれの
領域を
合わせると
こうです
29
今度は
等号で
結んであってですよ

30
左辺 xの入ってるとこは
絶対値を
外してみたところ
片方だけ
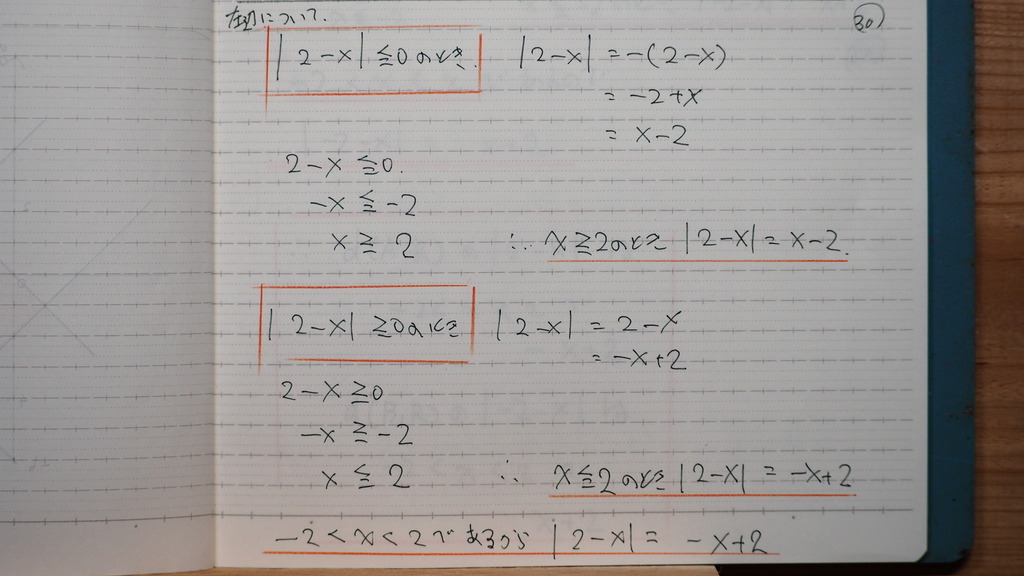
31
右辺の xの入った
絶対値を
外してみたところ
やはり
片方だけ
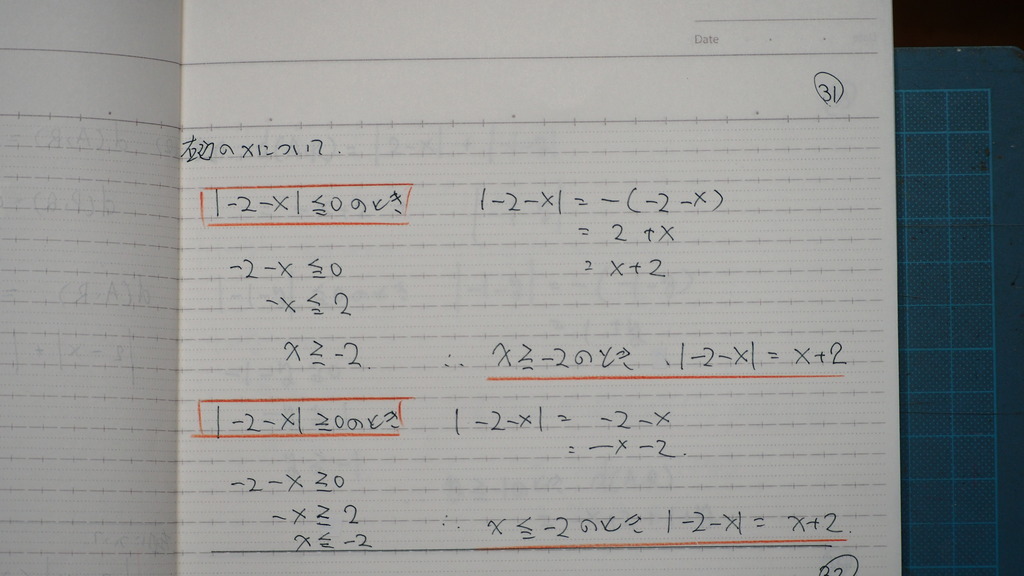
32
であるので
左辺 右辺で
xの入ってるとこは
左辺は -x+2
右辺は x+2

33
左辺の yの入った
絶対値は
-1 以上か
-1 以下か
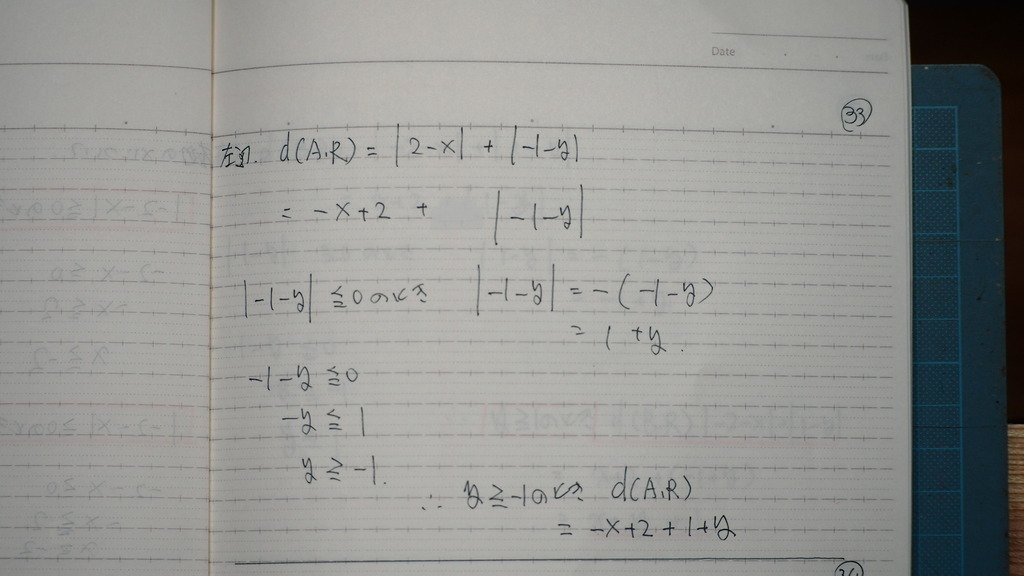
34
整理すると
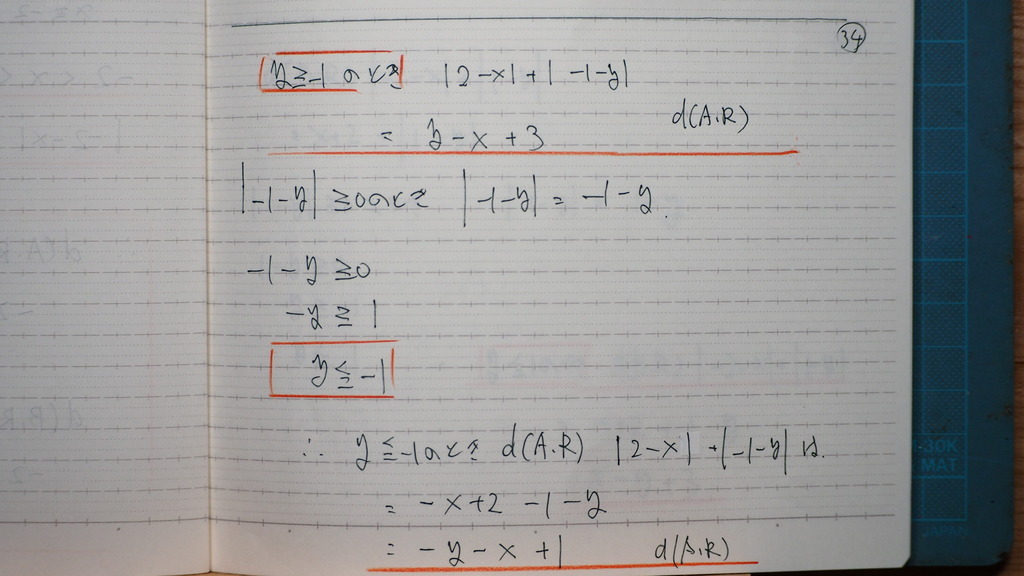
35
右辺の yの入った
絶対値を外すと
1以上の時
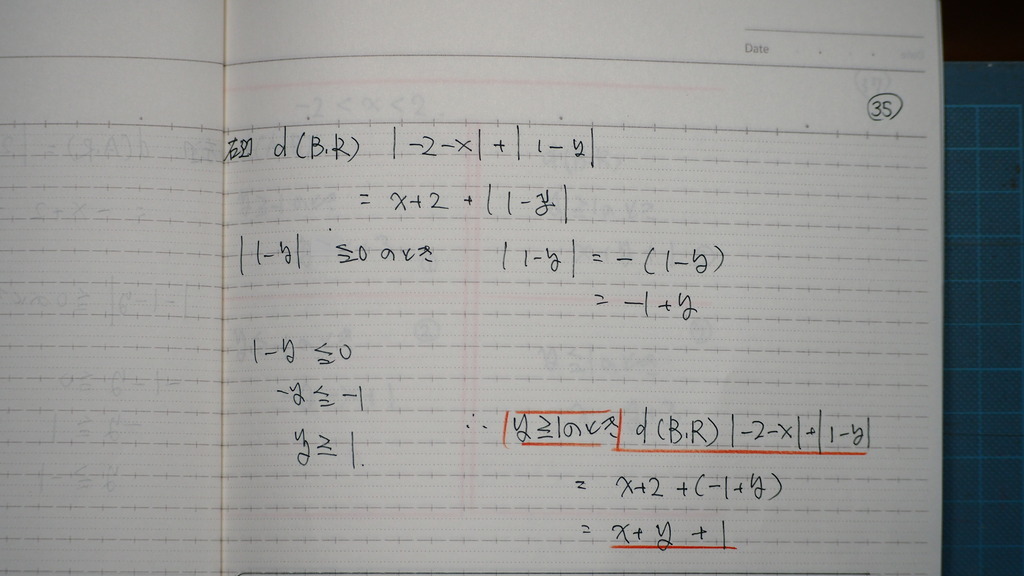
36
1以下
の時
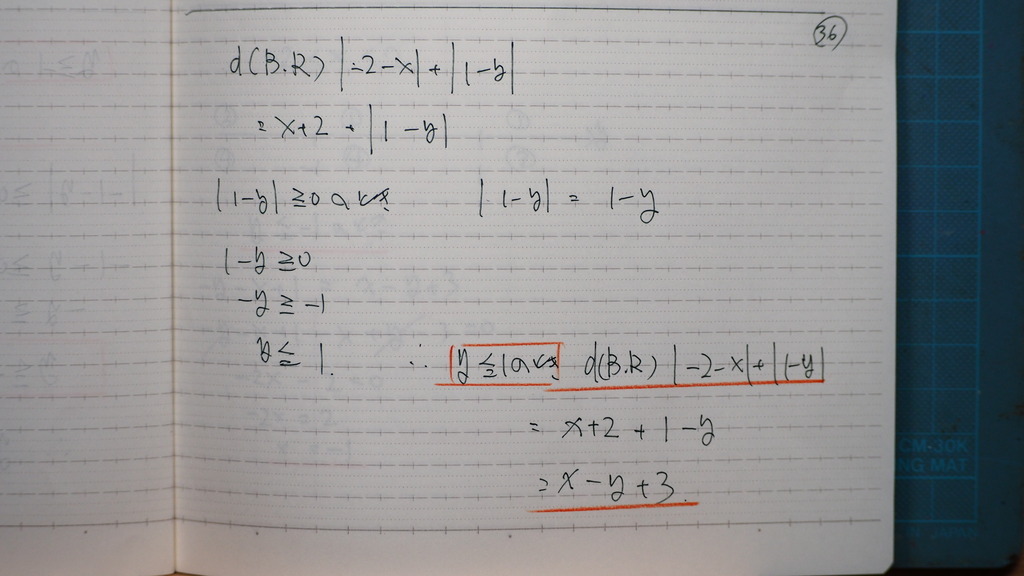
37
整理すると

38
これを
yの値で
場合分けして
等号で
結んで
②④ ➀④ ➀③
3っに 場合分け
yが -1以下の時
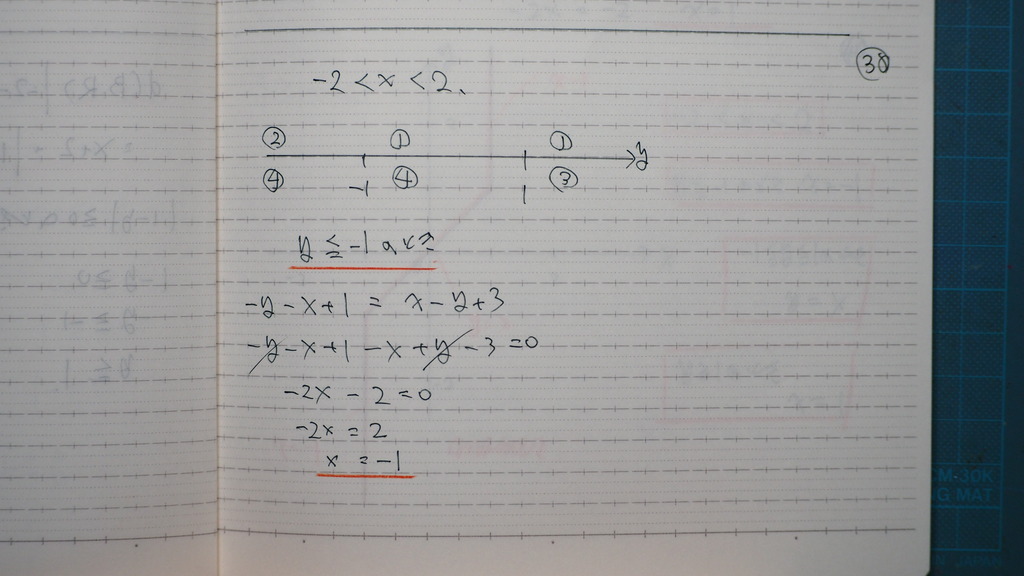
39
yが -1以上 1以下の時
yが 1以上の時
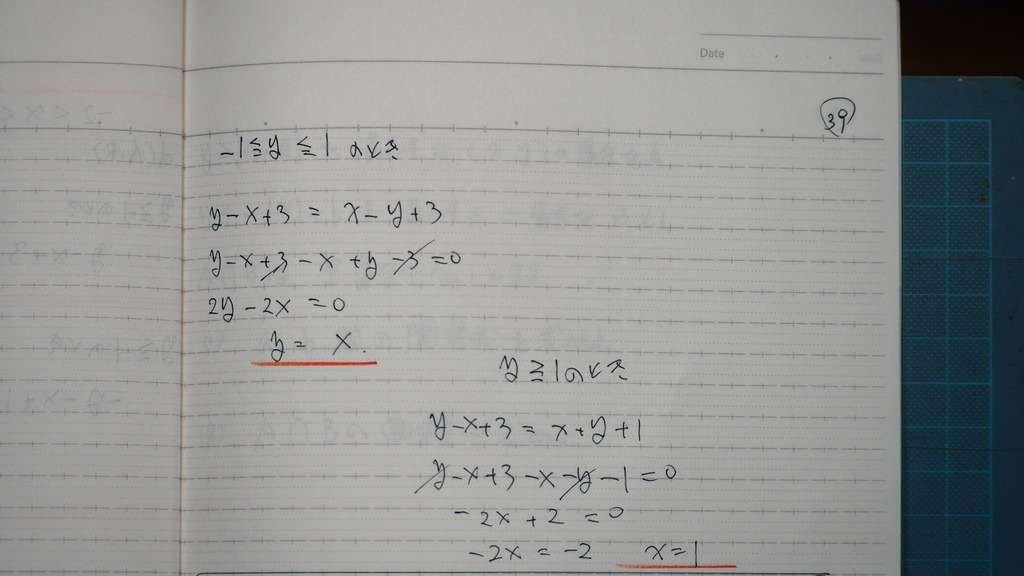
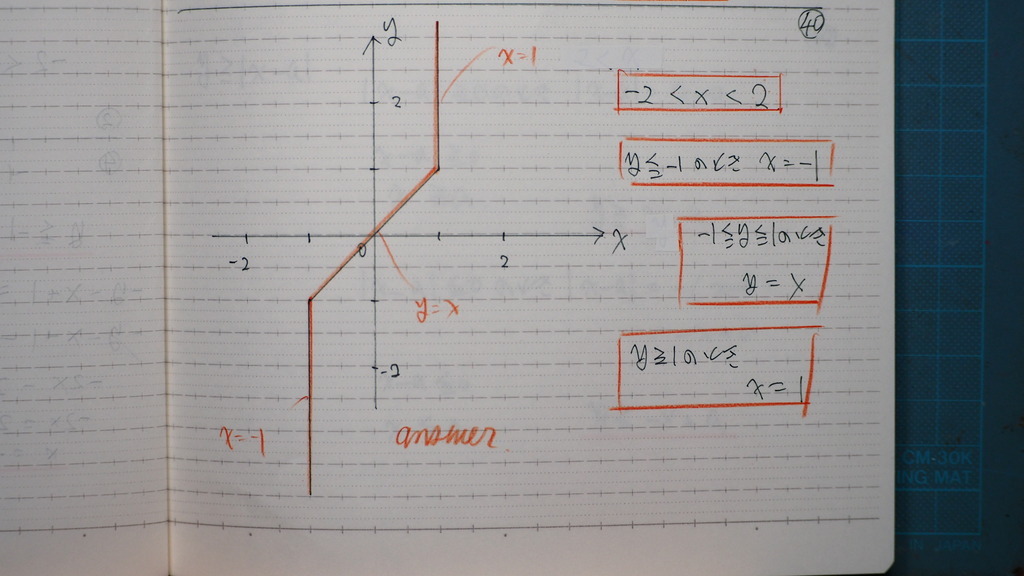
40
図にすると
こんな感じで
41
問題

42
先ずさ
グラフに してみるじゃナイスカ

43
一本目
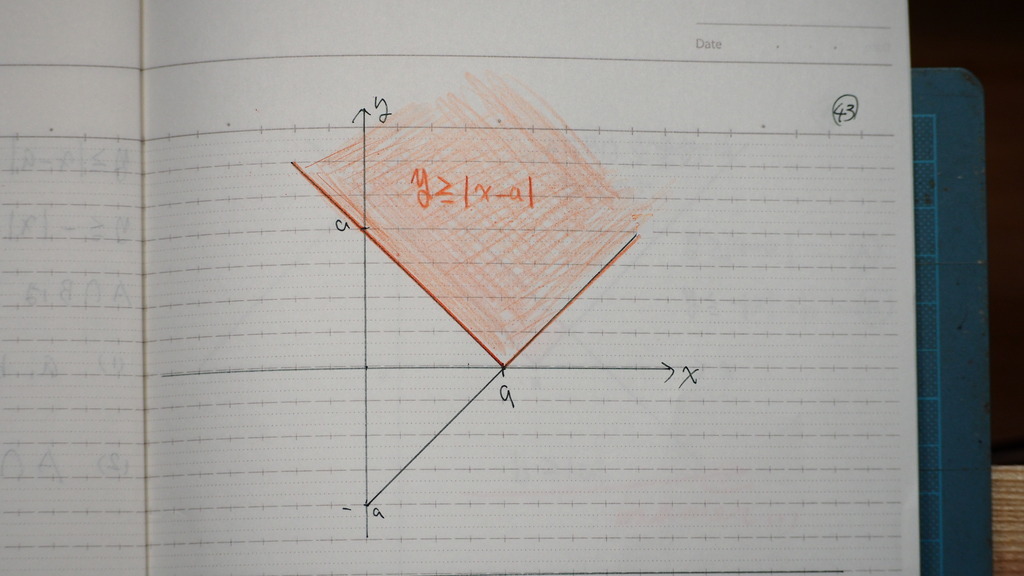
44
2本目
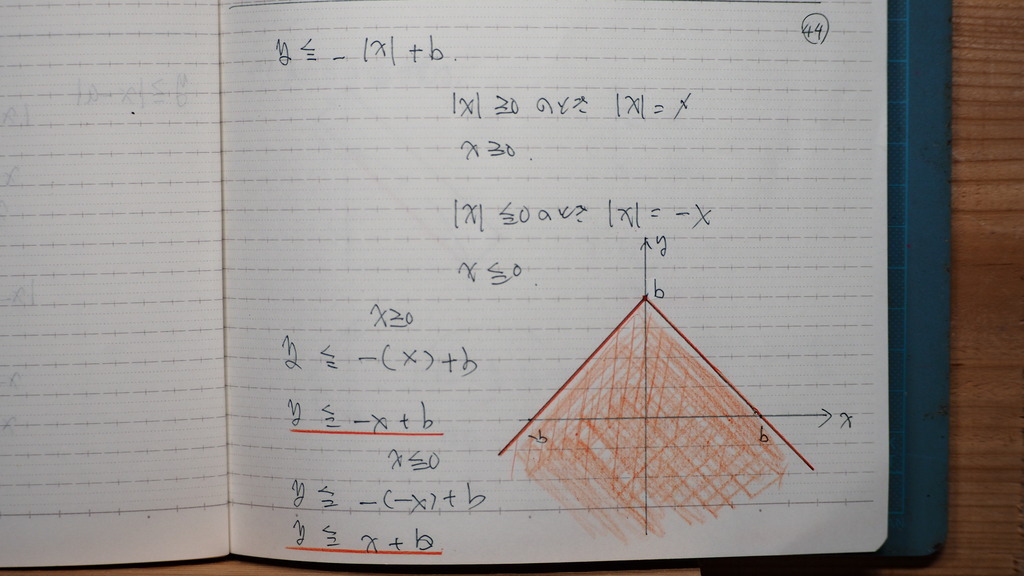
45
それで
AとBの交わり
A ∩ B (キャップ)は
空集合ではない
なので
bが a以上 うえにないと
aが マイナスの時も考えて
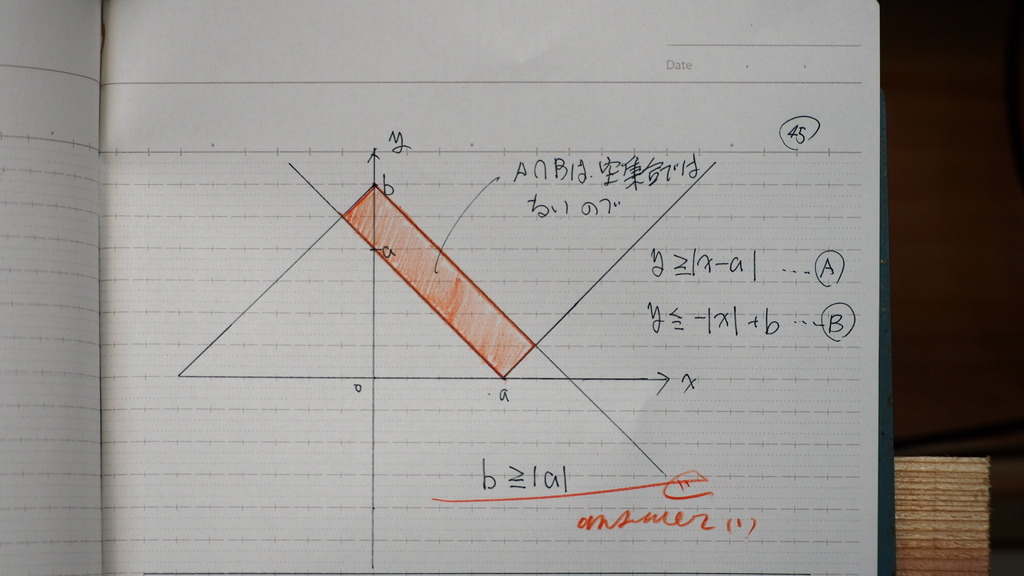
46
長方形の面積なので
直角2等辺三角形の
比の値から
辺の 長さを 出してきて
縦横掛けると
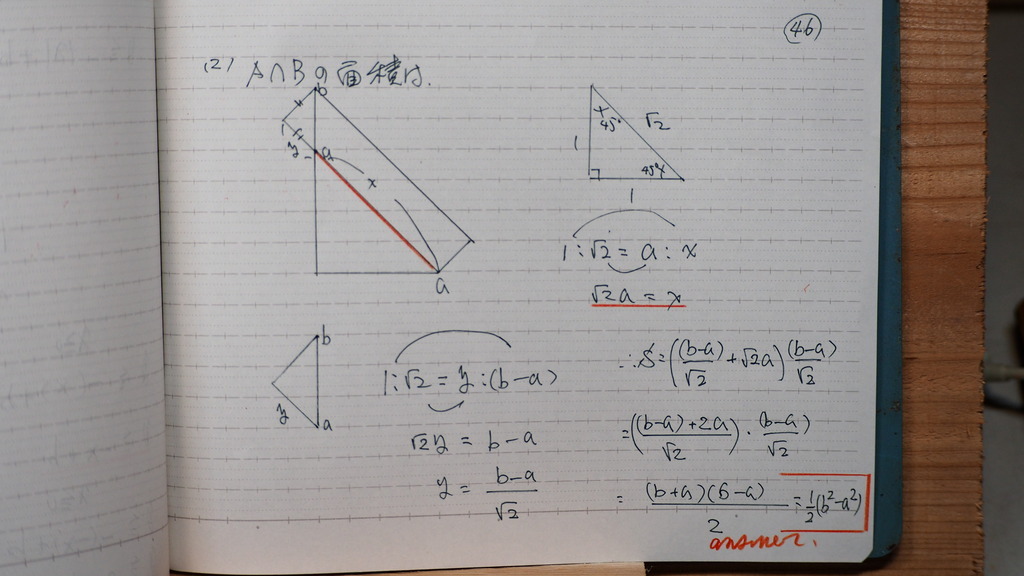
お疲れ様です。
図形と方程式
不等式と領域 (1)
01
どんな感じかと言うと
不等式で示された
領域が
グラフの 上 か 下 か
その見つけ方
y大なりは グラフに上
y小なりは グラフの下
わからないときは
特定の点を 式に代入して
不等式の 向きを 確認する
02
例えば
これらは
こんな場合は
03
こんな 表現で
聞かれるときも
04
キャップは 交わり
カップは 全て
05
動点の時は
06
以上踏まえまして
問題
(1) (2) の
不等式の 示す 領域を
図示せよ
07
(ア)
1次不等式
2次元の直線
3は y切片
傾きが -2
で
グラフの 境界を含み 下側
08
大丈夫かどうか
特定の点を
代入したらば
09
グラフは
こんな感じ
式変形する前の
不等式に
特定の点を代入して
調べると
10
こんなかんじ
11
√のとこは
半円
半円より 下側で
-2から 2までの間
注意点は
x=-2 x=2は
境界線含む
12
さっきの 2番目
(イ)の問題と
おなじでは ないです
13
類題 行ってみましょう
14
グラフを 書いて
点を代入して
確認すると
15
( 画像 未 修正必要 )
場合分けして
16
グラフの 境界線を含み
この範囲
17
実数条件を調べて
18
半円の 周を含み 下側
19
問題
20
A.N.S
アフタ ・ n ・ショー
21
三つ 式ができて来て
グラフを
書くじゃナイスカ
22
この
赤い 領域に 在れば オッケイ
23
問題
これはさ
場合分けが 大変そうだね
24
x系の 絶対値を外すと
2通り
25
y系の絶対値を 外すと
2通り
26
4組に 場合を分けて
まず 2組
27
もう2組
28
それぞれの
領域を
合わせると
こうです
29
今度は
等号で
結んであってですよ
30
左辺 xの入ってるとこは
絶対値を
外してみたところ
片方だけ
31
右辺の xの入った
絶対値を
外してみたところ
やはり
片方だけ
32
であるので
左辺 右辺で
xの入ってるとこは
左辺は -x+2
右辺は x+2
33
左辺の yの入った
絶対値は
-1 以上か
-1 以下か
34
整理すると
35
右辺の yの入った
絶対値を外すと
1以上の時
36
1以下
の時
37
整理すると
38
これを
yの値で
場合分けして
等号で
結んで
②④ ➀④ ➀③
3っに 場合分け
yが -1以下の時
39
yが -1以上 1以下の時
yが 1以上の時
40
図にすると
こんな感じで
41
問題
42
先ずさ
グラフに してみるじゃナイスカ
43
一本目
44
2本目
45
それで
AとBの交わり
A ∩ B (キャップ)は
空集合ではない
なので
bが a以上 うえにないと
aが マイナスの時も考えて
46
長方形の面積なので
直角2等辺三角形の
比の値から
辺の 長さを 出してきて
縦横掛けると
お疲れ様です。
2023年01月12日
22041 大人のさび落とし 空間座標とベクトル 最終ページ 空間図形(2)
大人のさび落とし
空間座標とベクトル
空間図形(2)
01
問題
こんな感じに
立方体から
中点を選んで
連結すると
正六角形になるんだって
証明して

02
であるから
座標を使ってじゃナイスカ
こんな感じで
2分の にするより
2倍しちゃえば
楽だから
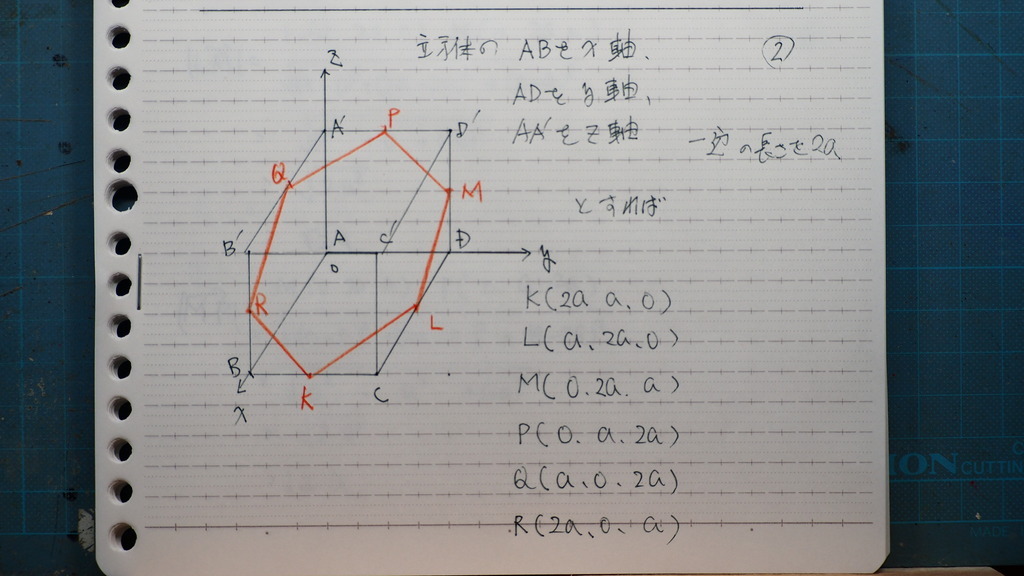
03
座標を
設定したところで
それぞれの
辺の長さが
等しいか
二点間の距離の計算が
6問

04
同だ
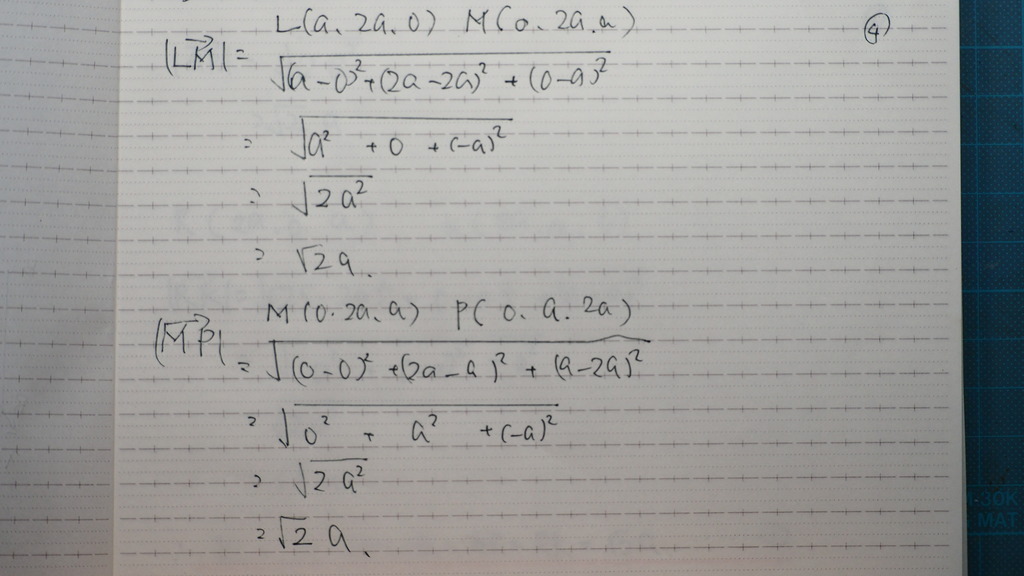
05
同だ
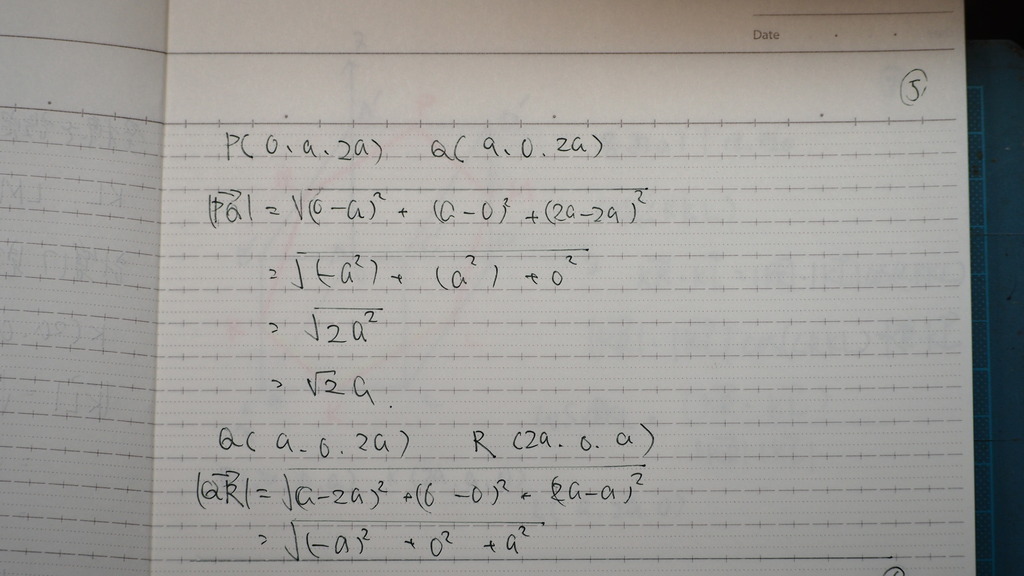
06
みんな 同じだった
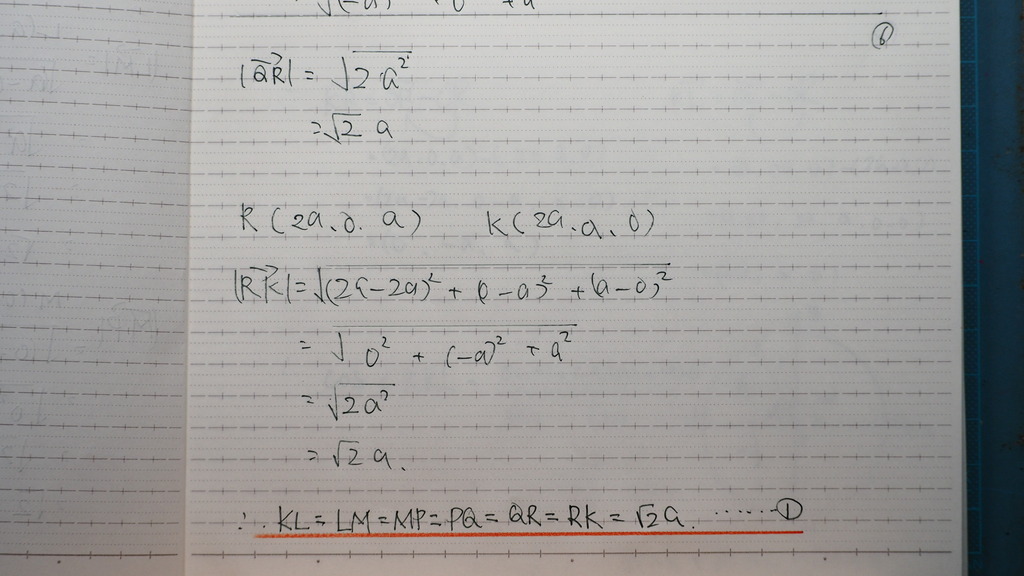
07
今度は
隣り合う辺の
なす角を
計算すると
計算問題 6問
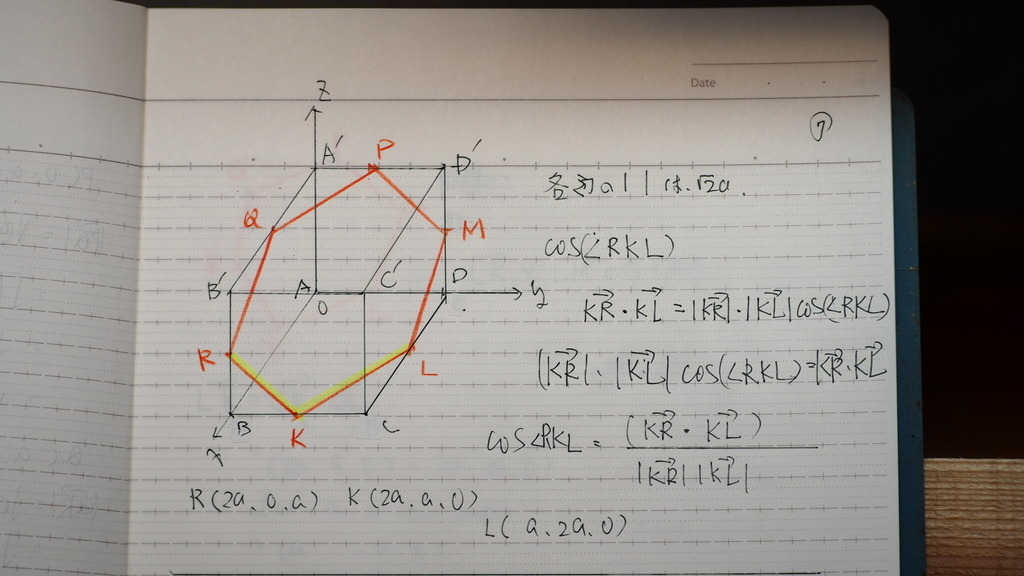
08
120ど

09
同様に
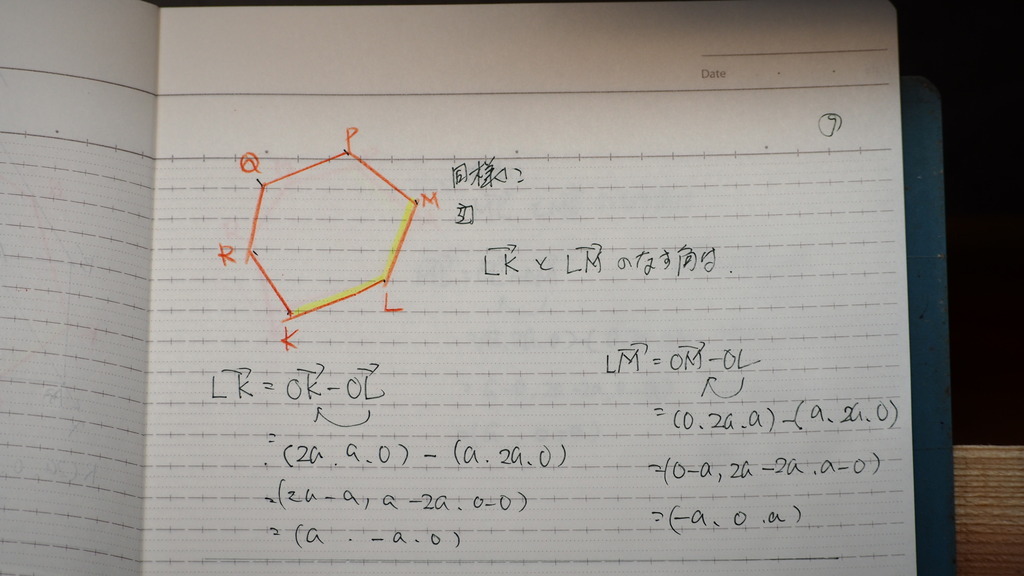
10
120度
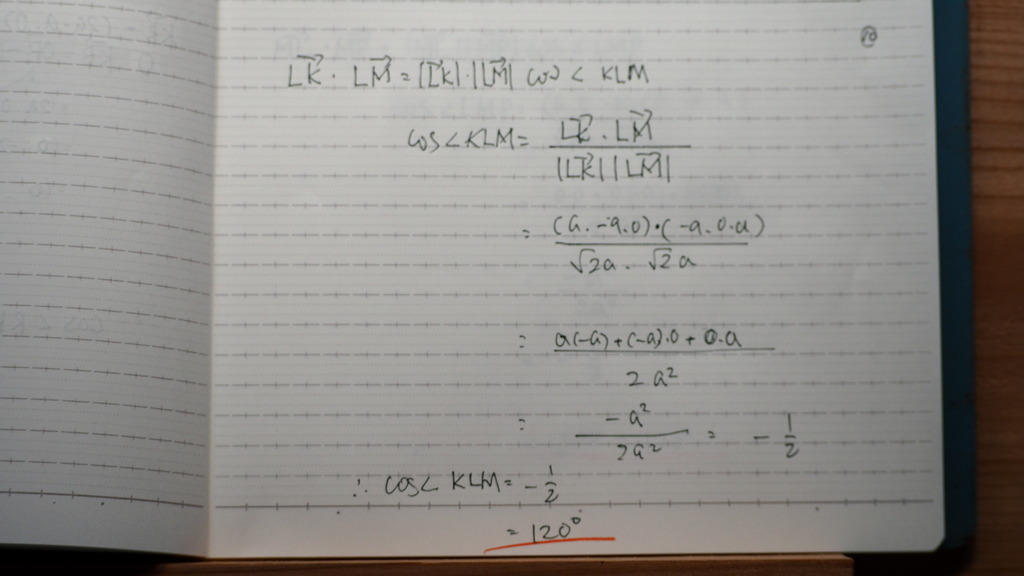
11
同様に
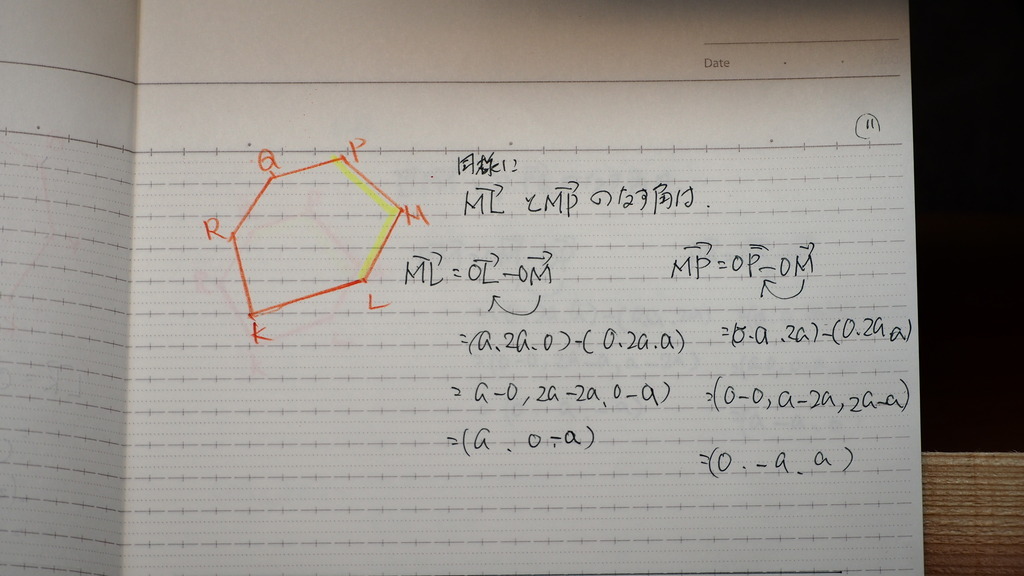
12
120ど
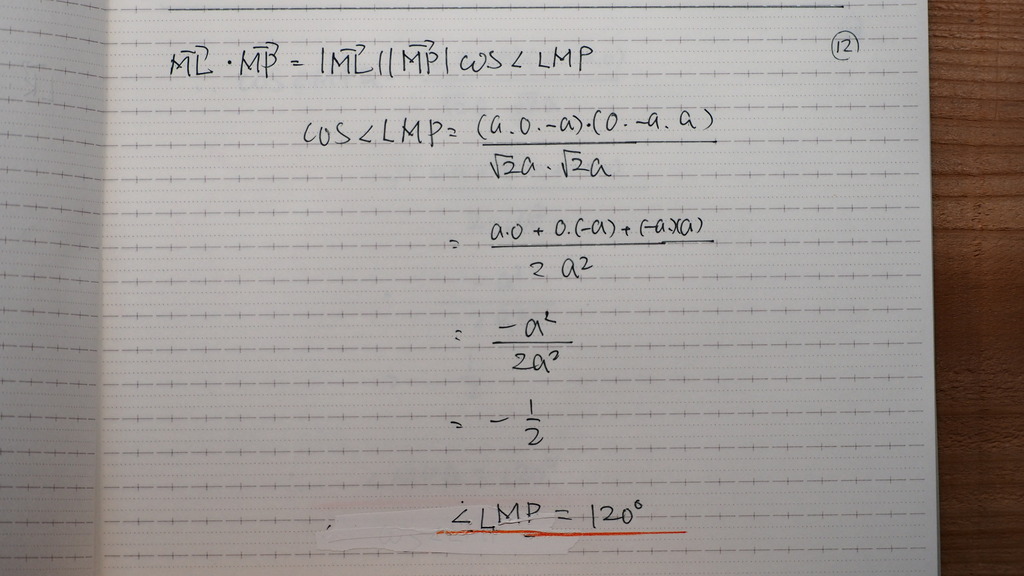
13
同様に
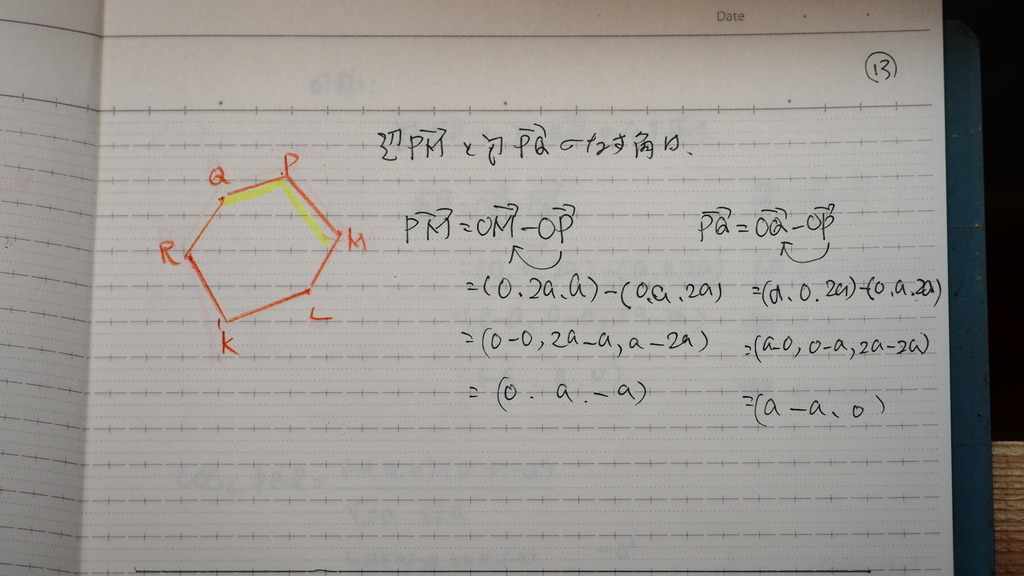
14
120度
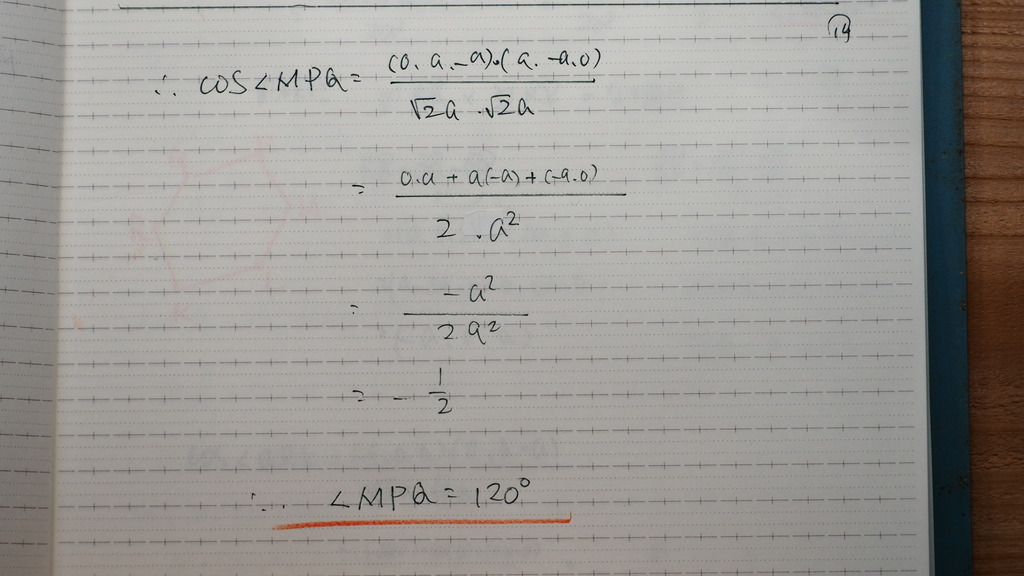
15
同様に
120度
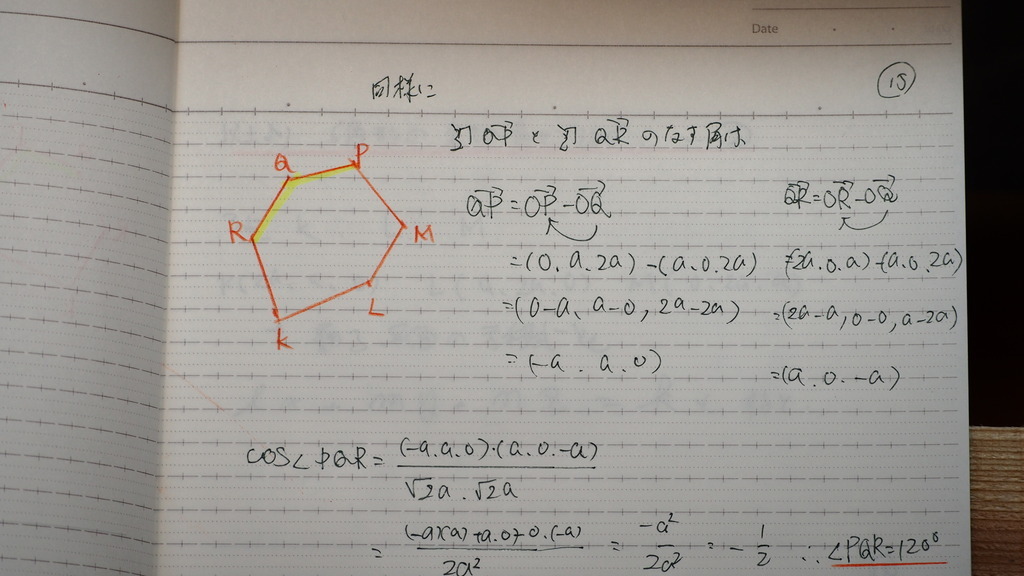
16
同様に
これはさ
実際に
過去に 某大学の入試に
出たんだそうだけど
やっぱり
全部 計算したのかな
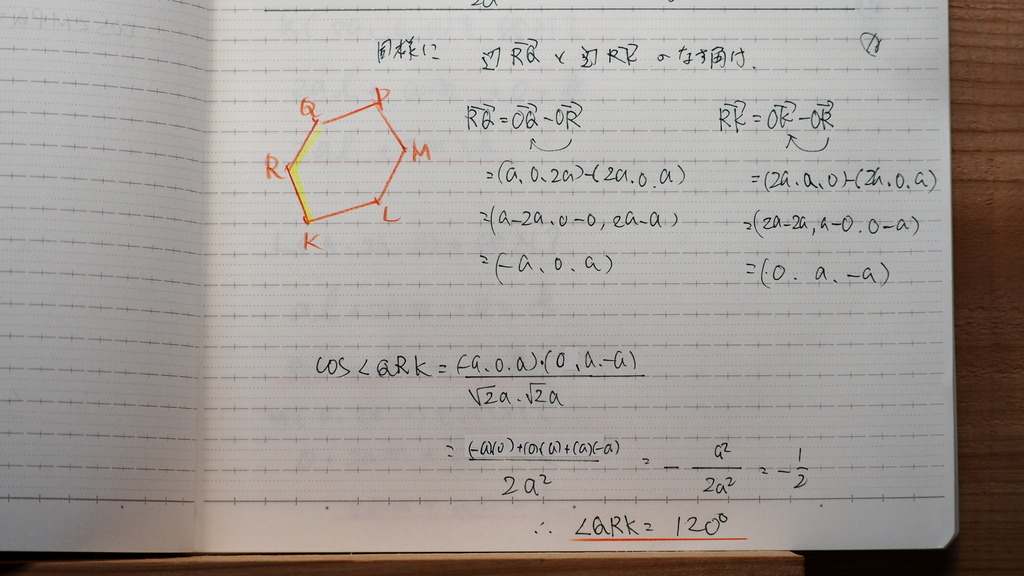
17
で さらに
3点を ひっぱり出してきて
平面の方程式を
求めると

18
媒介変数表示形から

19
3本式が出て来て

20
法線ベクトルが
みんな同じだから
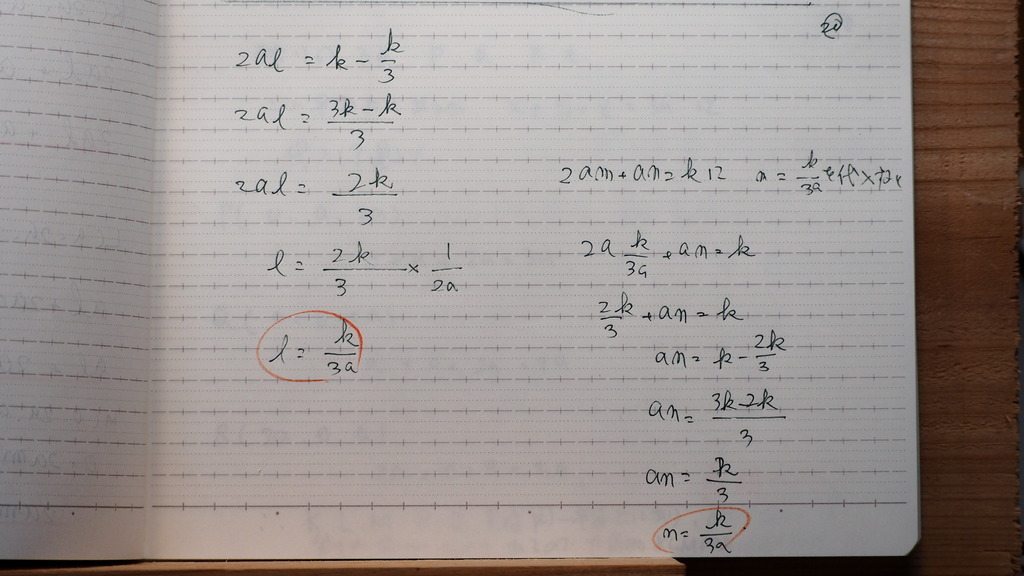
21
これが
平面の 方程式

22
残りの 3点を
ソレゾレ
代入したらば
全て
同一平面上にあるので
これはもう
正六角形だよ

23
問題

24
直線の 方程式は
こうだから

25
媒介変数表示形から
Z=0
を
代入して
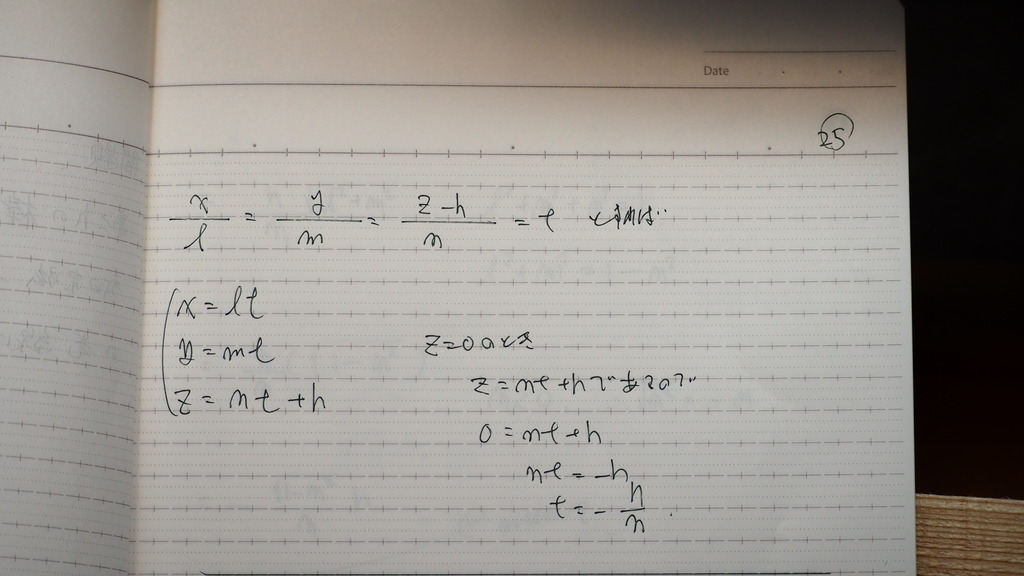
26
交点の 座標が出たので
影の 大きさは
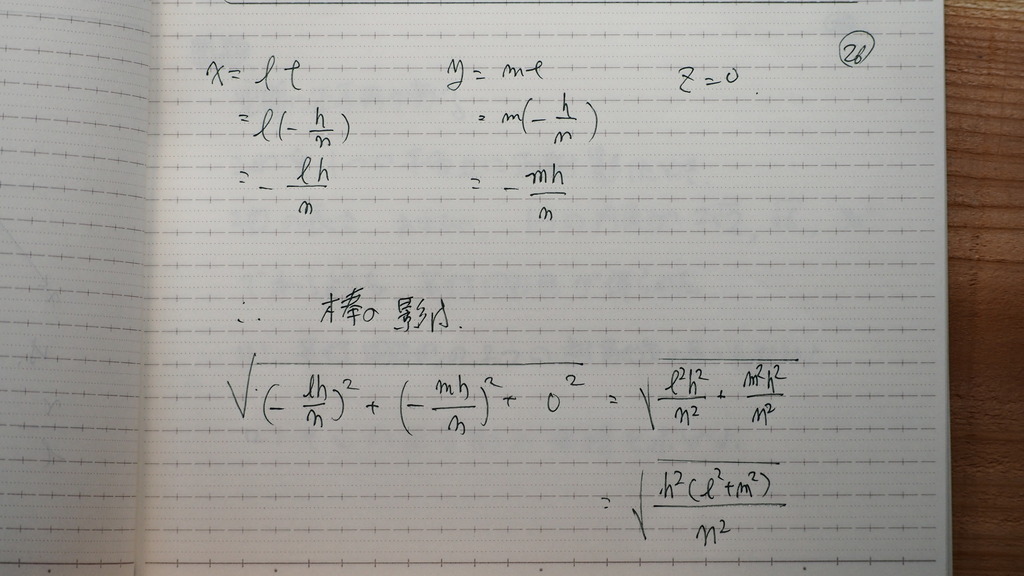
27
nは マイナスなんだね

28
問題
正方形を
平面に 正射影したんだって
そうしたら
影が
こんなで
平行四辺形になった
対角線のながさは
元の正方形の面積は

29
余弦定理を
使えば
早いよね
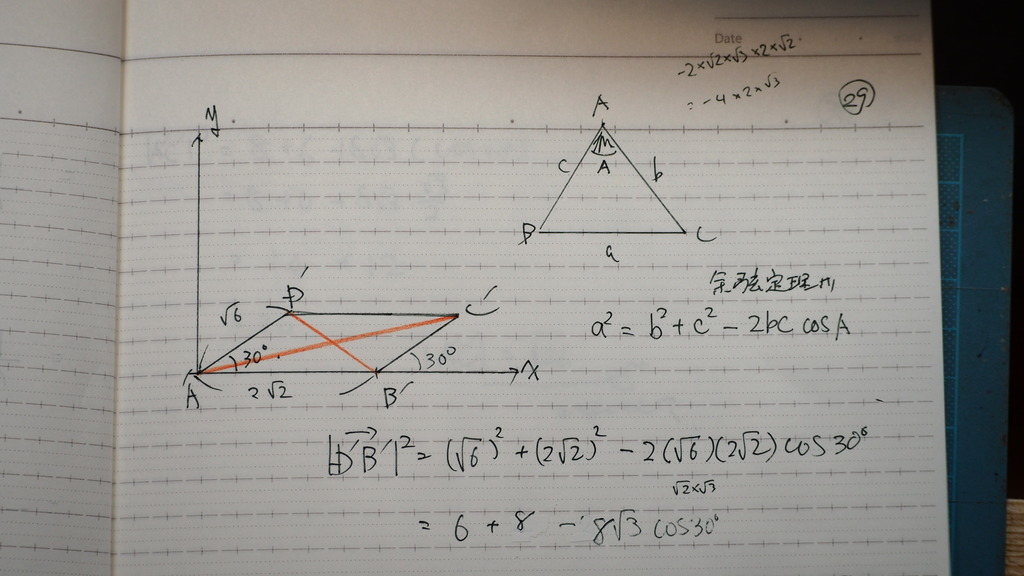
30
平行四辺形だからさ
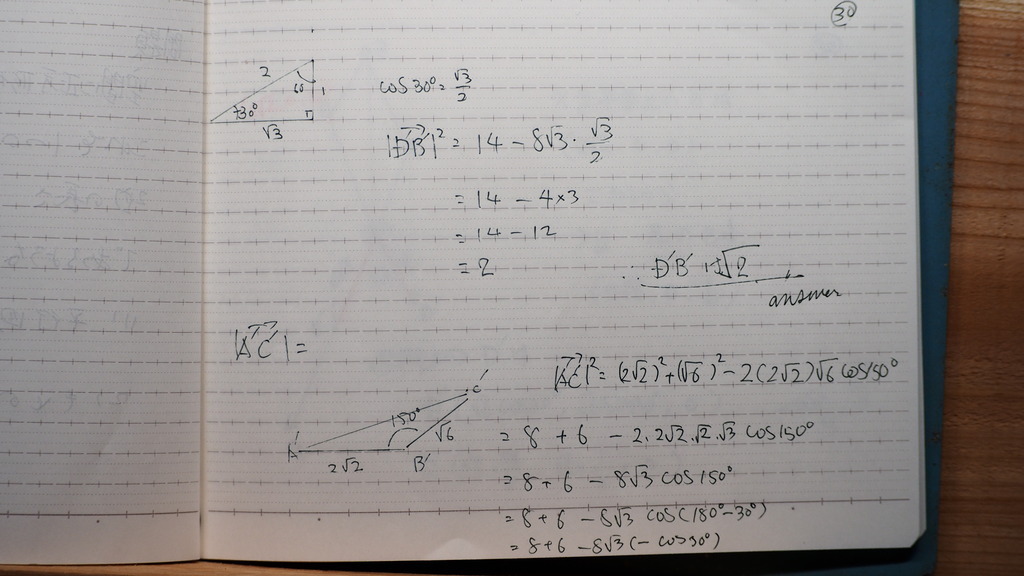
31
余弦定理は
2乗だからさ
ルートで
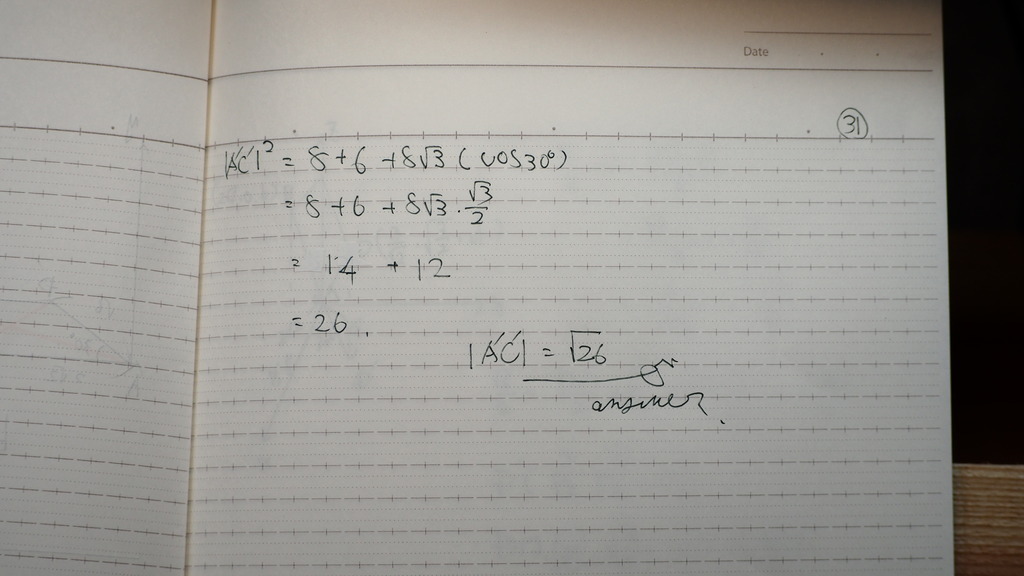
32
問題は
次なんだけどね
真上から
ななめに 成ってる
正方形を
投影してるでしょ
だから
座標は こんなんでさ
ただ
計算しやすいように
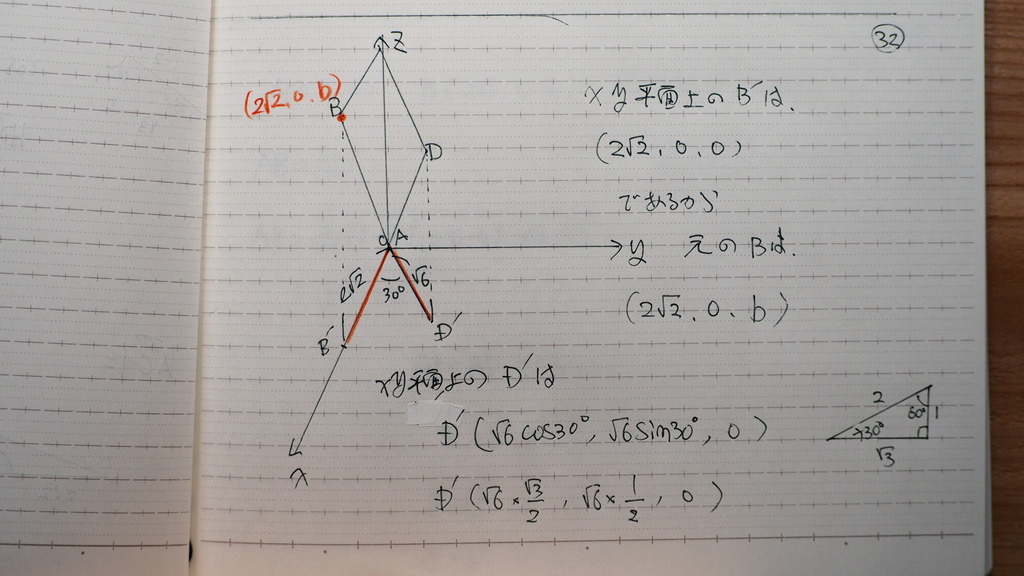
33
わざと
√2を 入れる形で
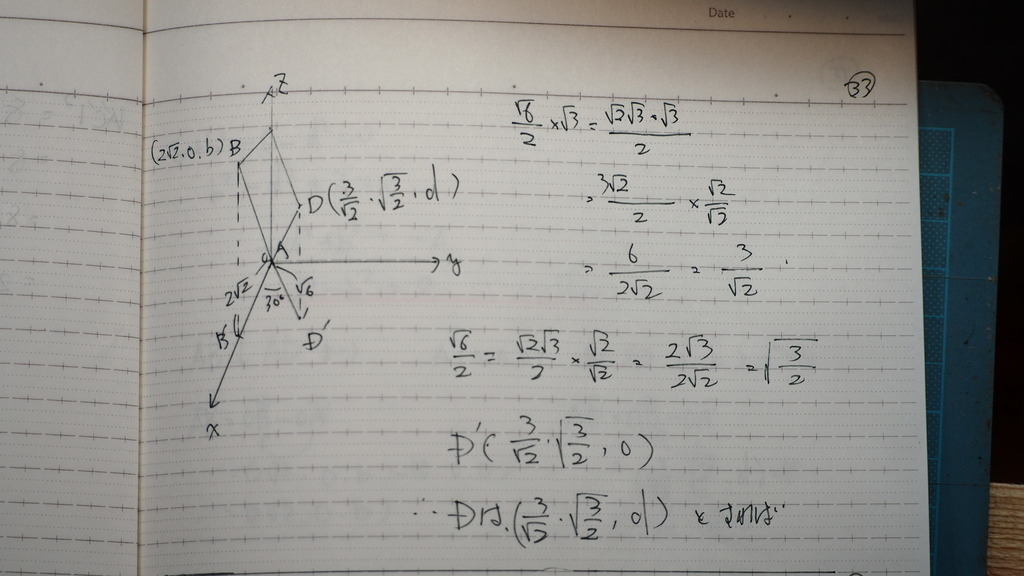
34
そうでもないか
で
なんか式が出て来て
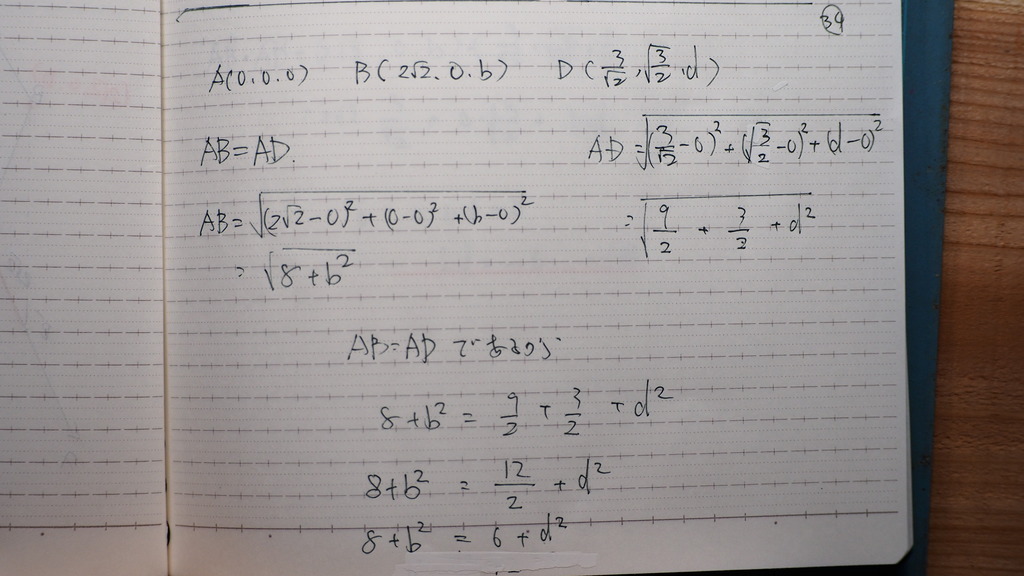
35
もう一本
内積の
成分の計算から
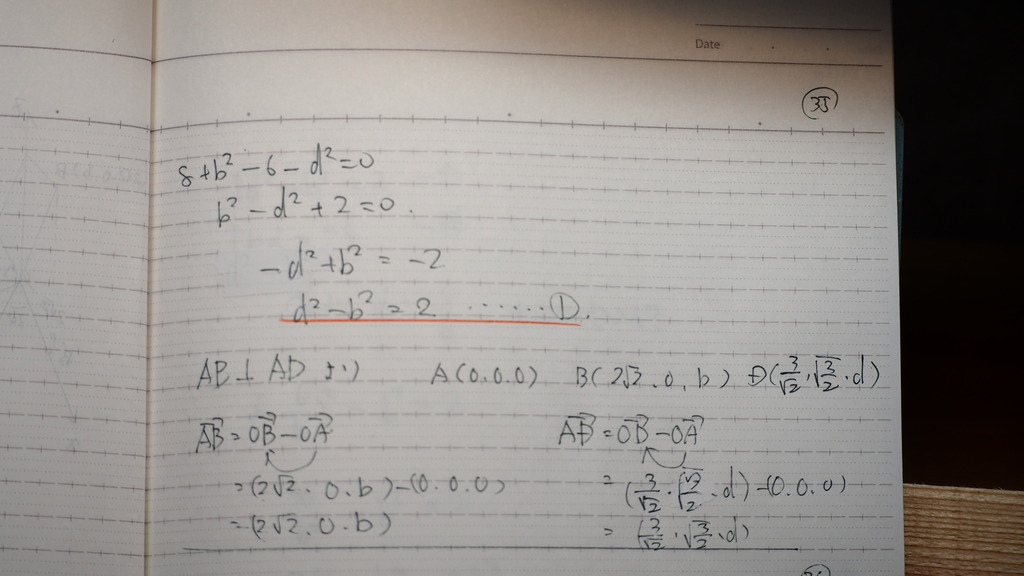
36
式が出て来て

37
これを
解くと
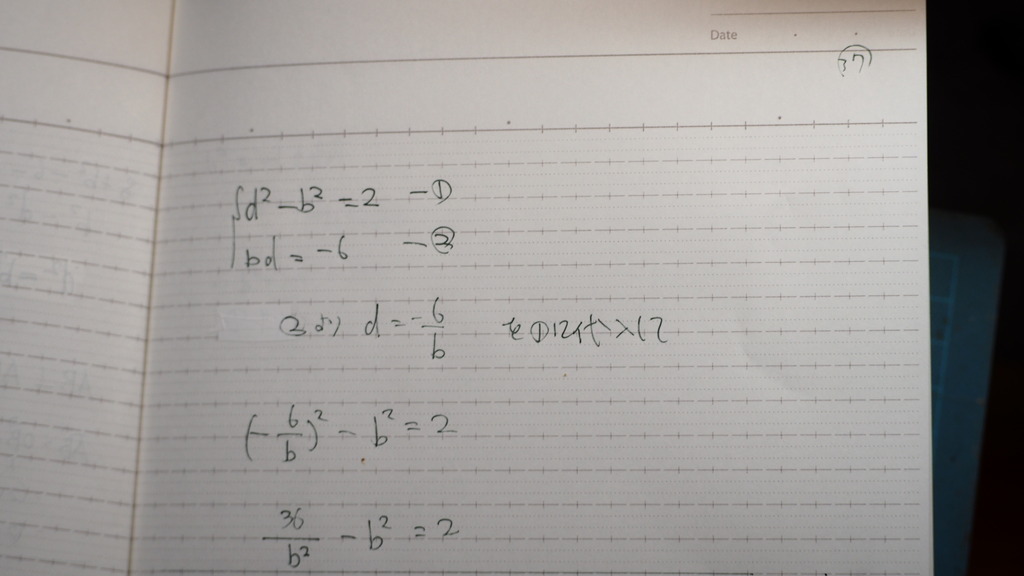
38
4乗だからさ
置き換えて
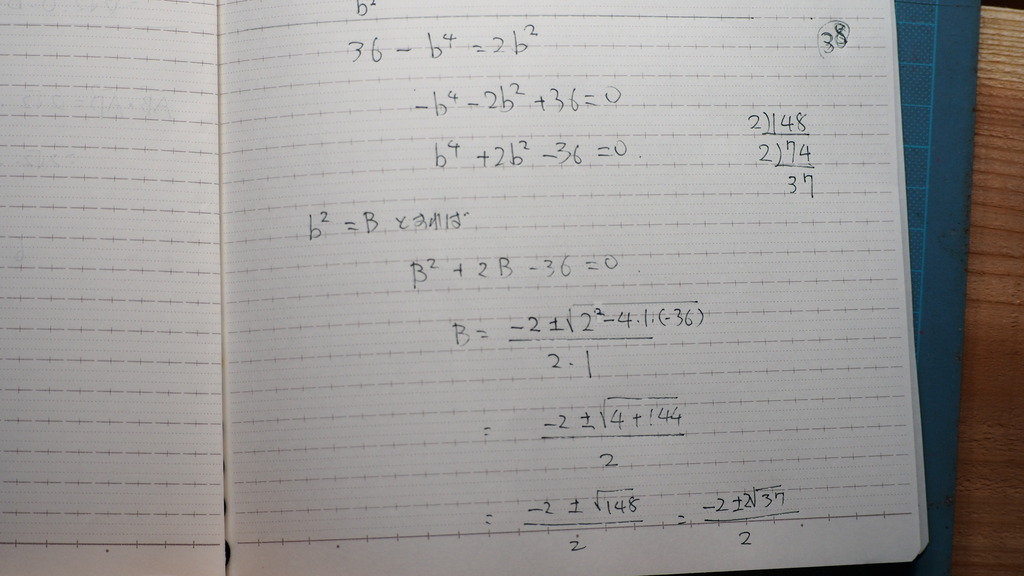
39
長さだから
マイナスは
まずいよな
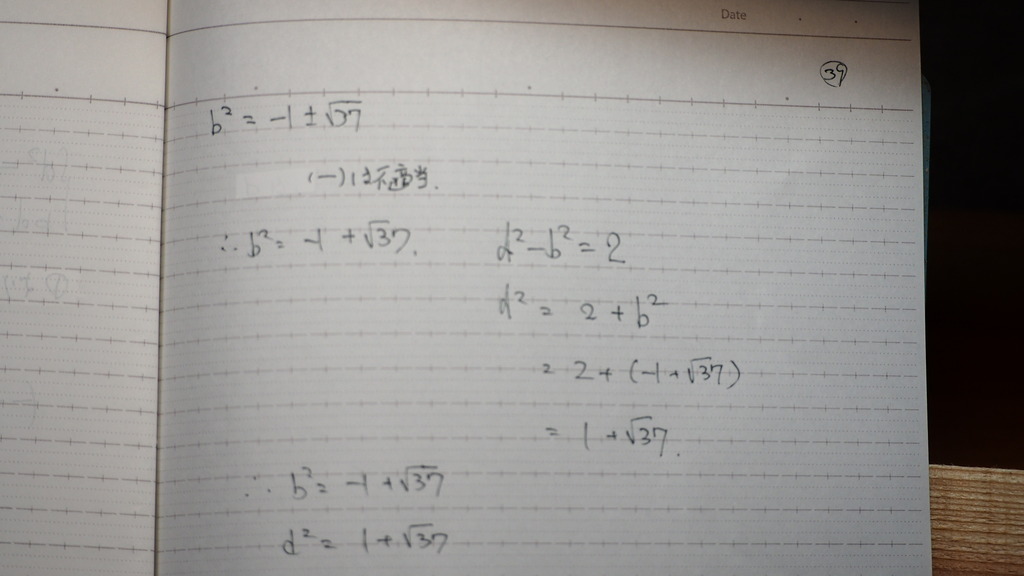
40
で
面積 ダメかな と思ったんだけど
正方形だから
ABの二乗で
行けるんだからさ
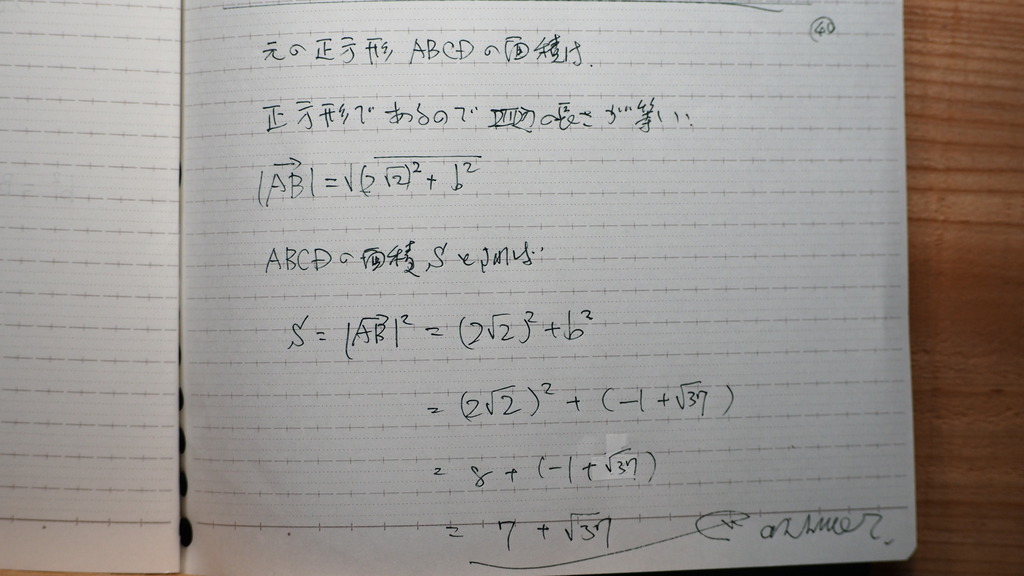
b2乗に -1+√37を 代入したら
7+√37
お疲れ様です。
空間座標とベクトル
空間図形(2)
01
問題
こんな感じに
立方体から
中点を選んで
連結すると
正六角形になるんだって
証明して
02
であるから
座標を使ってじゃナイスカ
こんな感じで
2分の にするより
2倍しちゃえば
楽だから
03
座標を
設定したところで
それぞれの
辺の長さが
等しいか
二点間の距離の計算が
6問
04
同だ
05
同だ
06
みんな 同じだった
07
今度は
隣り合う辺の
なす角を
計算すると
計算問題 6問
08
120ど
09
同様に
10
120度
11
同様に
12
120ど
13
同様に
14
120度
15
同様に
120度
16
同様に
これはさ
実際に
過去に 某大学の入試に
出たんだそうだけど
やっぱり
全部 計算したのかな
17
で さらに
3点を ひっぱり出してきて
平面の方程式を
求めると
18
媒介変数表示形から
19
3本式が出て来て
20
法線ベクトルが
みんな同じだから
21
これが
平面の 方程式
22
残りの 3点を
ソレゾレ
代入したらば
全て
同一平面上にあるので
これはもう
正六角形だよ
23
問題
24
直線の 方程式は
こうだから
25
媒介変数表示形から
Z=0
を
代入して
26
交点の 座標が出たので
影の 大きさは
27
nは マイナスなんだね
28
問題
正方形を
平面に 正射影したんだって
そうしたら
影が
こんなで
平行四辺形になった
対角線のながさは
元の正方形の面積は
29
余弦定理を
使えば
早いよね
30
平行四辺形だからさ
31
余弦定理は
2乗だからさ
ルートで
32
問題は
次なんだけどね
真上から
ななめに 成ってる
正方形を
投影してるでしょ
だから
座標は こんなんでさ
ただ
計算しやすいように
33
わざと
√2を 入れる形で
34
そうでもないか
で
なんか式が出て来て
35
もう一本
内積の
成分の計算から
36
式が出て来て
37
これを
解くと
38
4乗だからさ
置き換えて
39
長さだから
マイナスは
まずいよな
40
で
面積 ダメかな と思ったんだけど
正方形だから
ABの二乗で
行けるんだからさ
b2乗に -1+√37を 代入したら
7+√37
お疲れ様です。
22040 大人のさび落とし 空間座標とベクトル 空間図形(1)
大人のさび落とし
空間座標とベクトル
空間図形(1)
01
3垂線の定理と言うのがあるですが

02
問題を
図にしてくと
平面上に
2本の直線があると
Hで 交わってる
そこへ
平面ほかのPから 垂線を
下したとき
2直線に
垂線が 垂直ならば
任意の 平面上の直線に対しても
垂直であることを
示せ
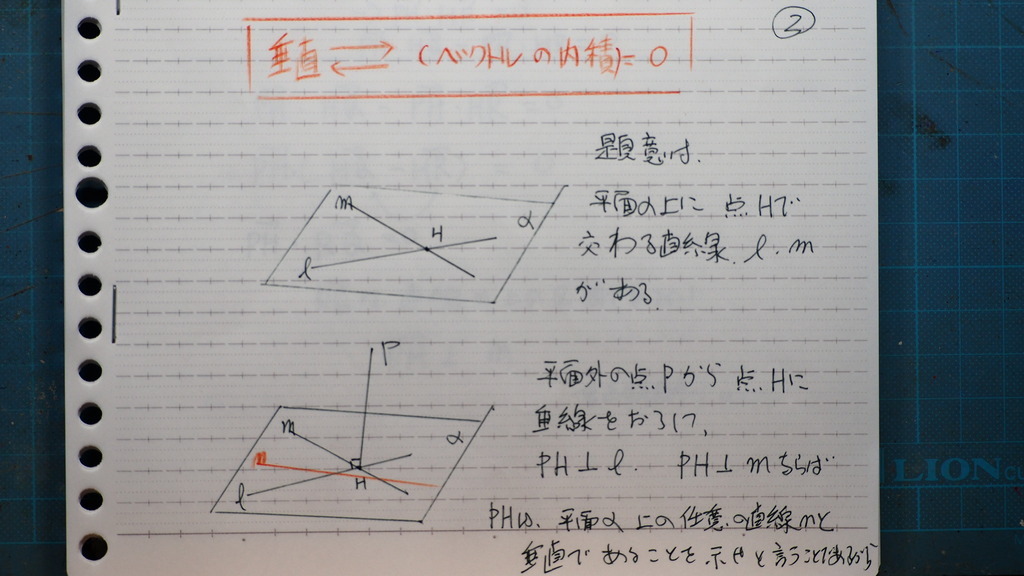
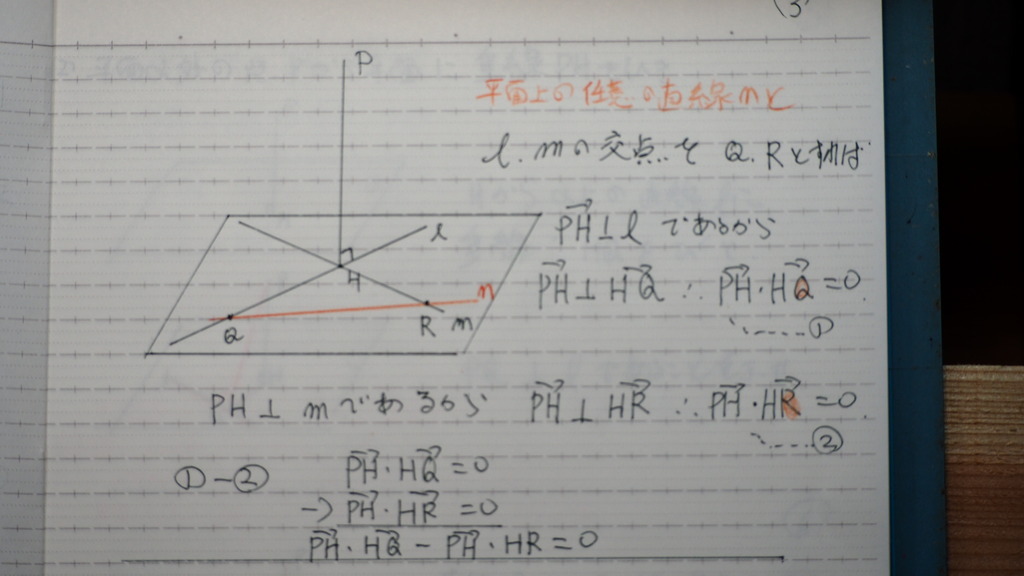
03
だから
平面上に
もう1本 n と言う
任意の直線を
引くじゃナイスカ
他の2直線との 交点を
Q,R とすれば
PH 垂直 L なので
L 上のベクトル HQとも
当然 垂直
PH 垂直 mであるから
m上のベクトル HR とも
当然垂直である
ここで
出てきた ➀②の式を
引算すると
PH で くくると
04
なんと
直線 n 上の ベクトル
RQ と 垂直になってる
だから
PH 垂直 n

05
今度は
Hから 平面上の 直線に
垂線を 引いたばあい
その交点を Qとすれが
PQ 垂直 L であるを
示せ

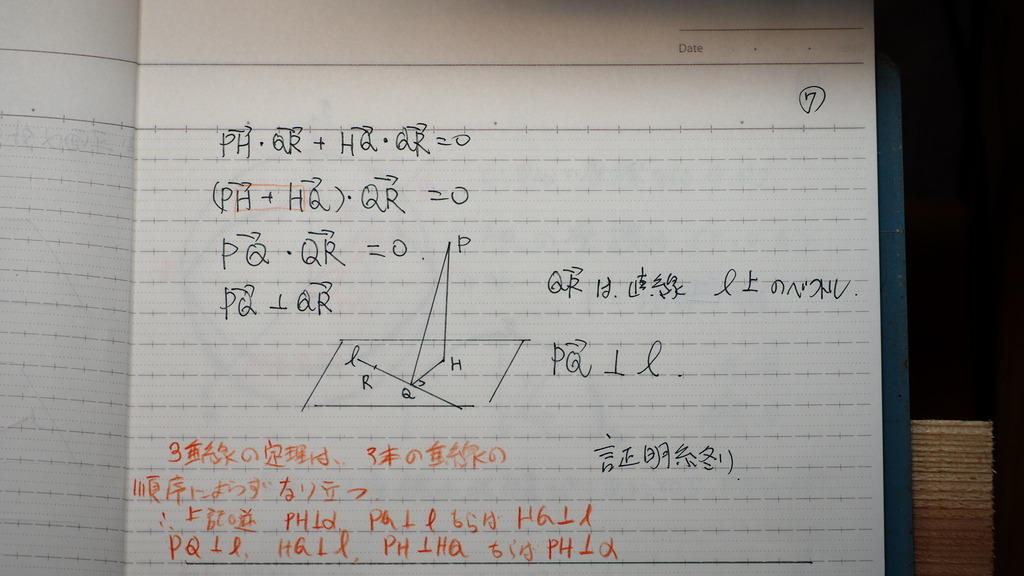
06
PH 垂直 Lであるから
とうぜん
L 上の ベクトル QRとも
垂直である
Hから Lに垂線を引いて
Qとしたのだから
当然
HQ 垂直 QRである
今度は
この ③④式を
足すと

07
なるんですよ
08
今度は
たまに 出て来そうな 問題です
地球は 丸かった
地球を 球と考えて
A地点を 北緯0度 東経0度
B地点を 北緯45度 統計35度
としたとき
地球の中心を 0として
角AOBは 何度か

09
空間座標を
考えるでしょ

10
普段から
こういう 計算してないと
あれって思いませんか
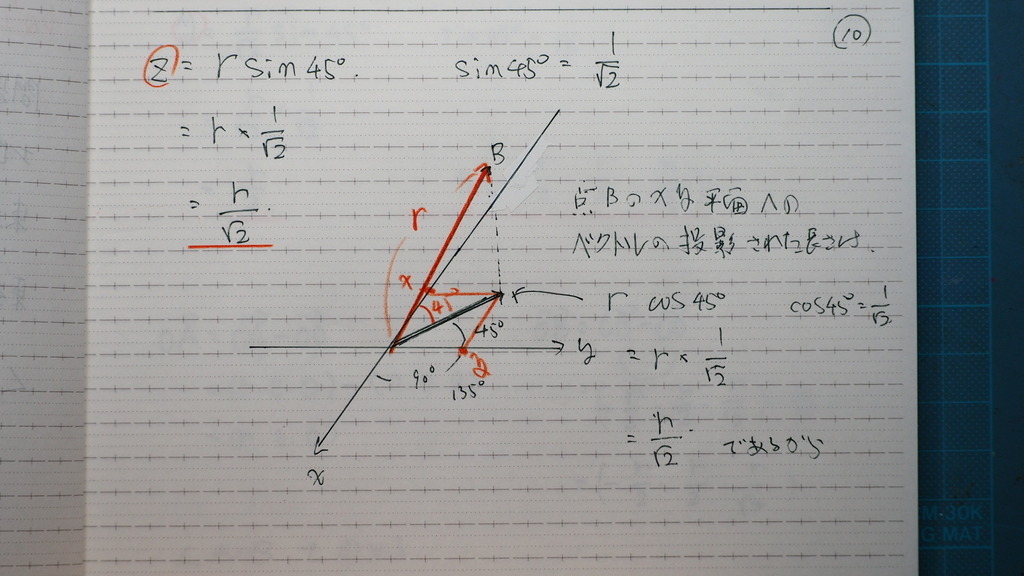
11
だからね
コレ イメージわかるかな
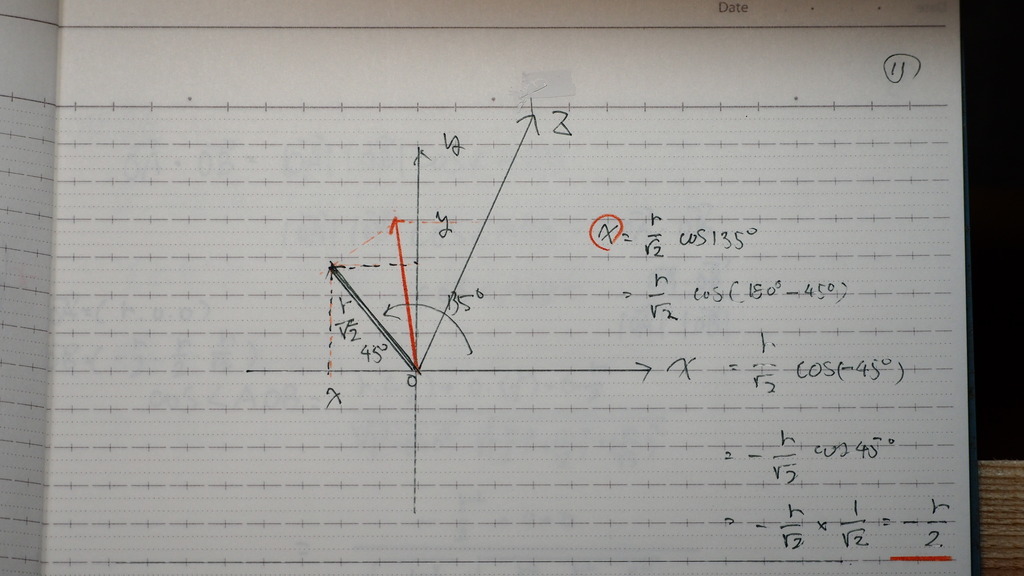
12
だからね
Bの座標は こうなんですよ
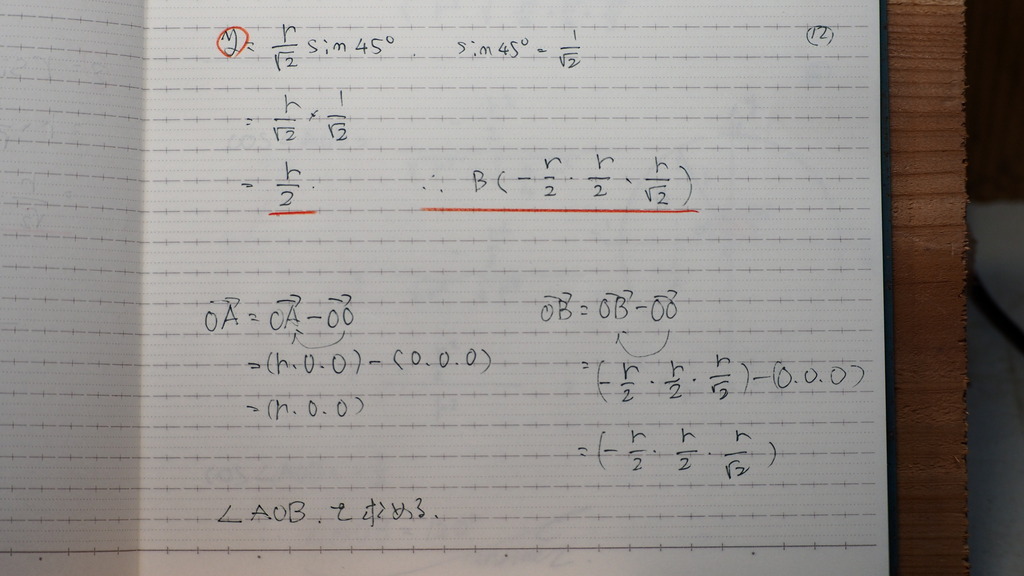
13
これで
空間座標の なす角を
求めると

14
120度
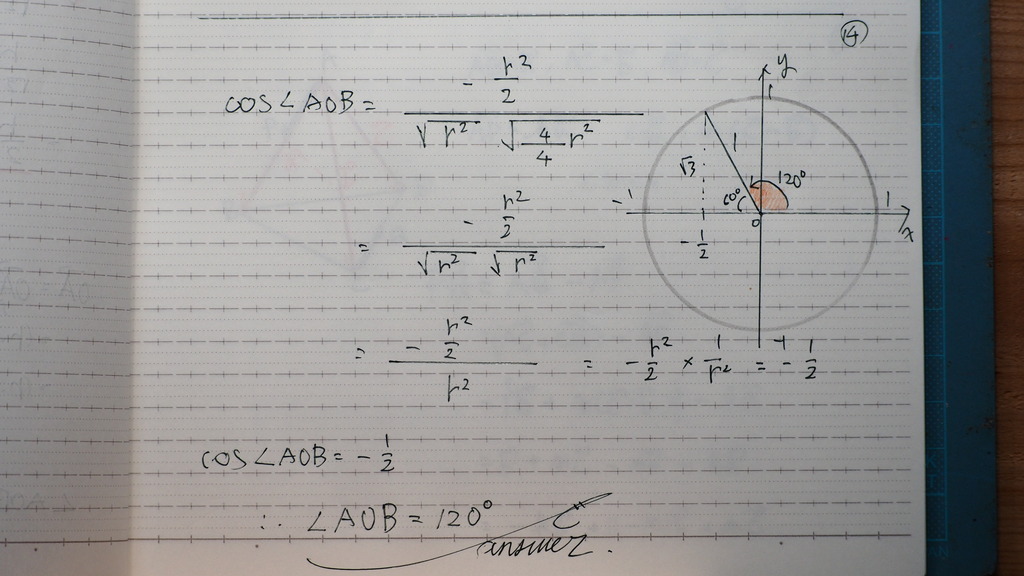
15
問題
これは
ベクトルの 設定が
出来れば
半分できた

16
まず 基本的な ベクトルは
こんな感じで
AP と CQ を
こんな感じにできれば

17
2乗で 内積を
展開してくと
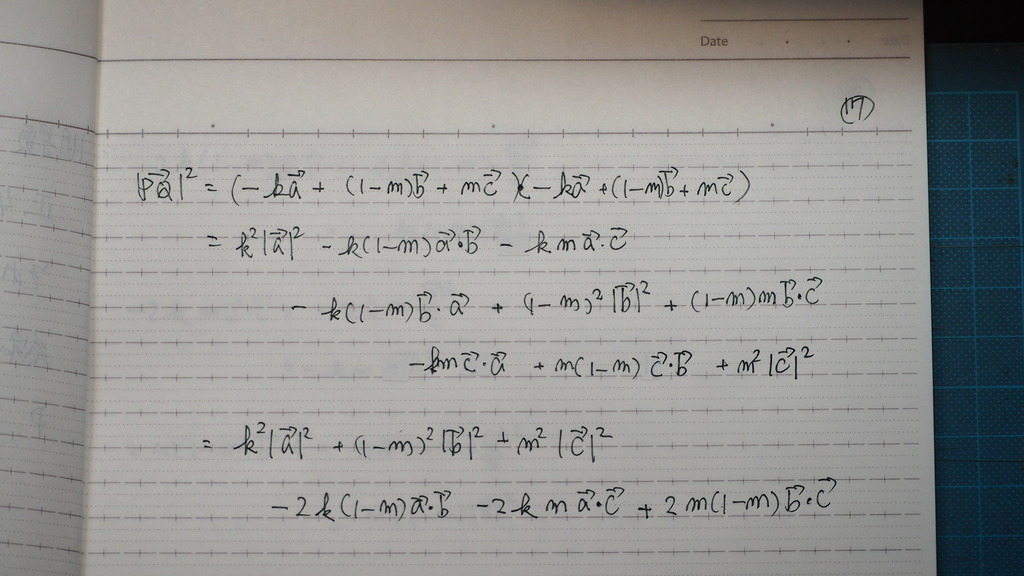
18
題意より
正四面体であるので
もうちょっと 簡単になる

19
こんな感じに
まとめて
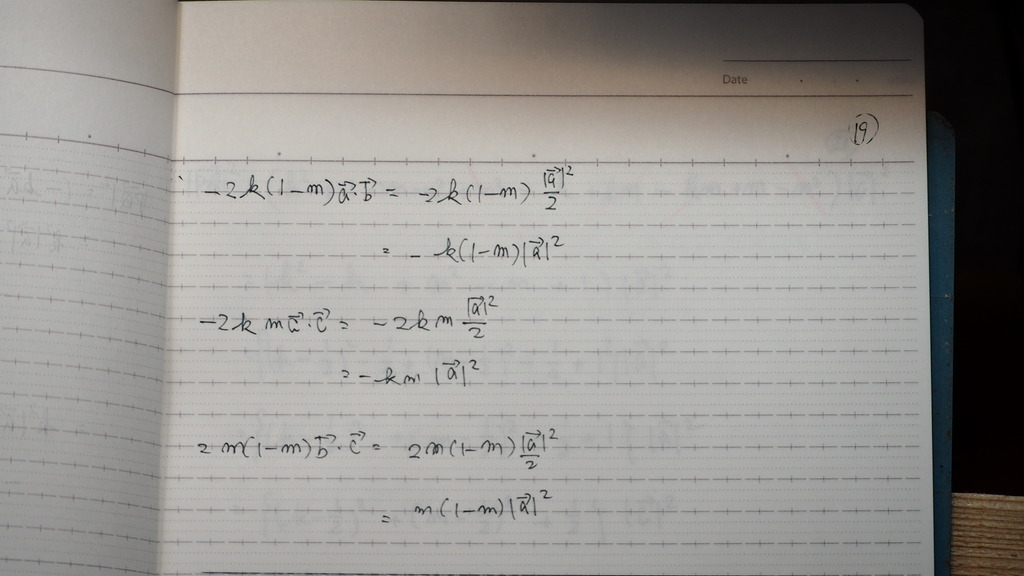
20
整理して
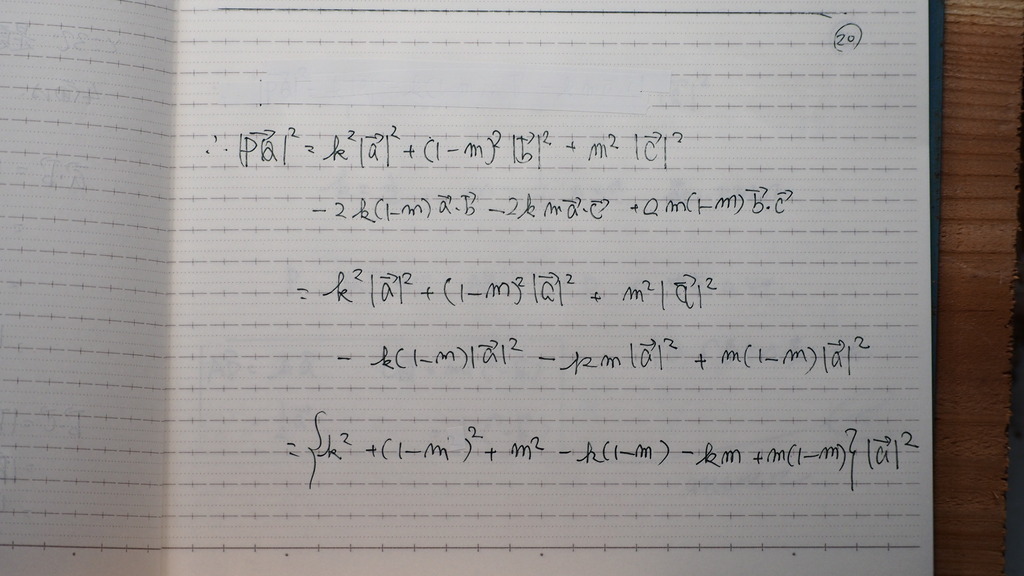
21
これをさ
平方を 作ると
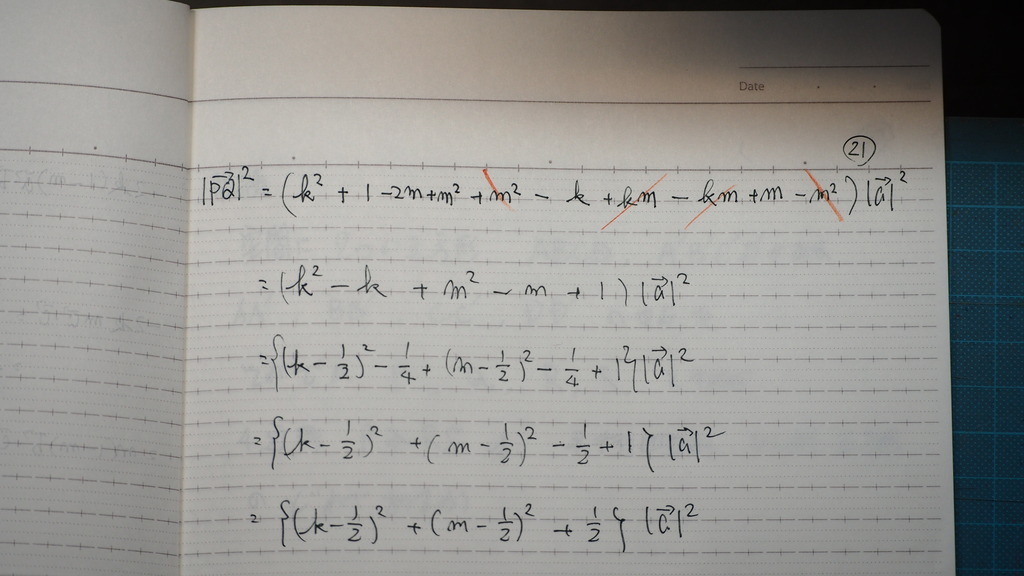
22
P,Qが それぞれ
中点の時
最初になる

23
問題

24
これはさ
中点の 連結定理で
計算したらば
PQは
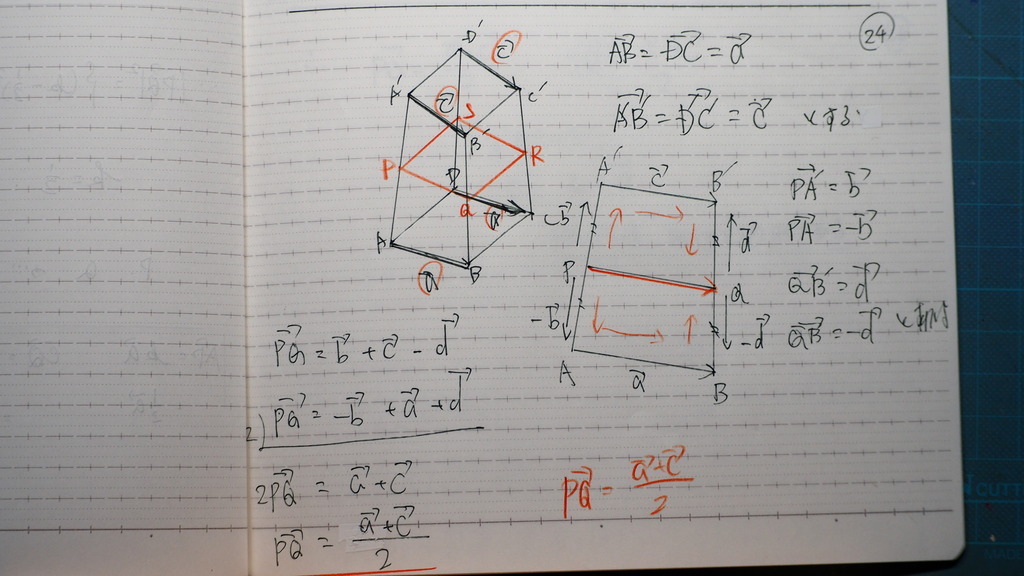
25
SRは
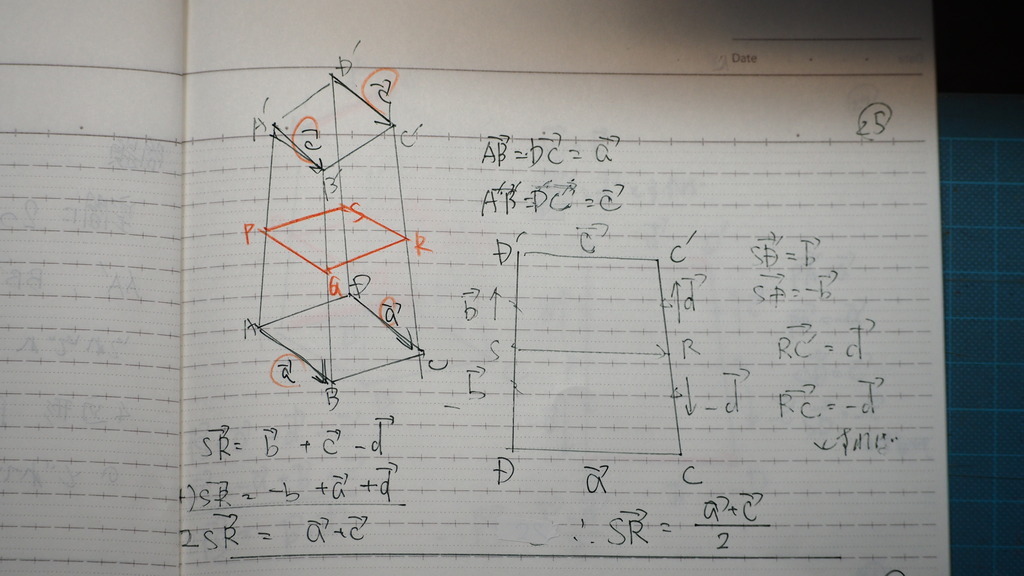
26
ここで
平行四辺形
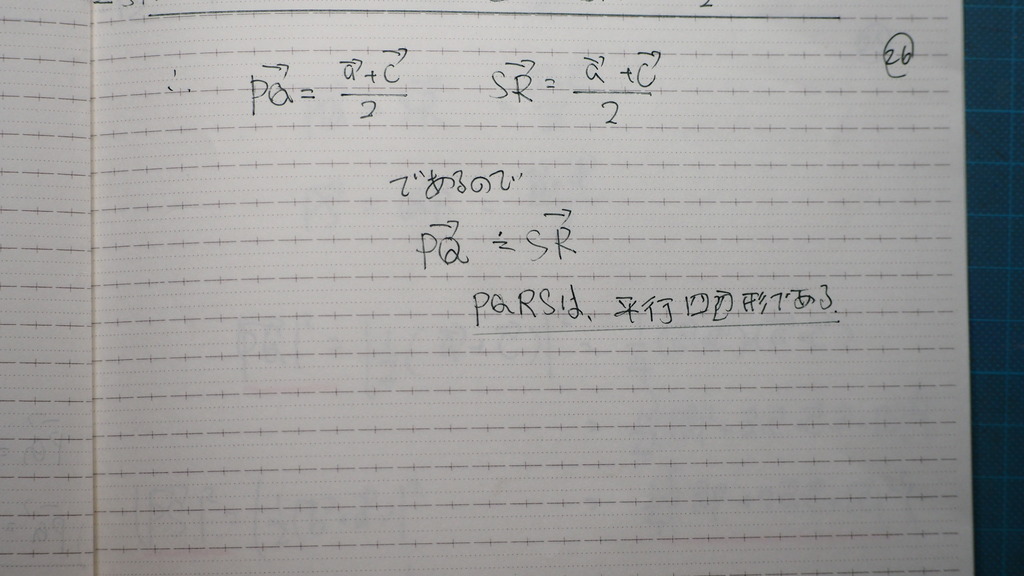
27
で
PSは
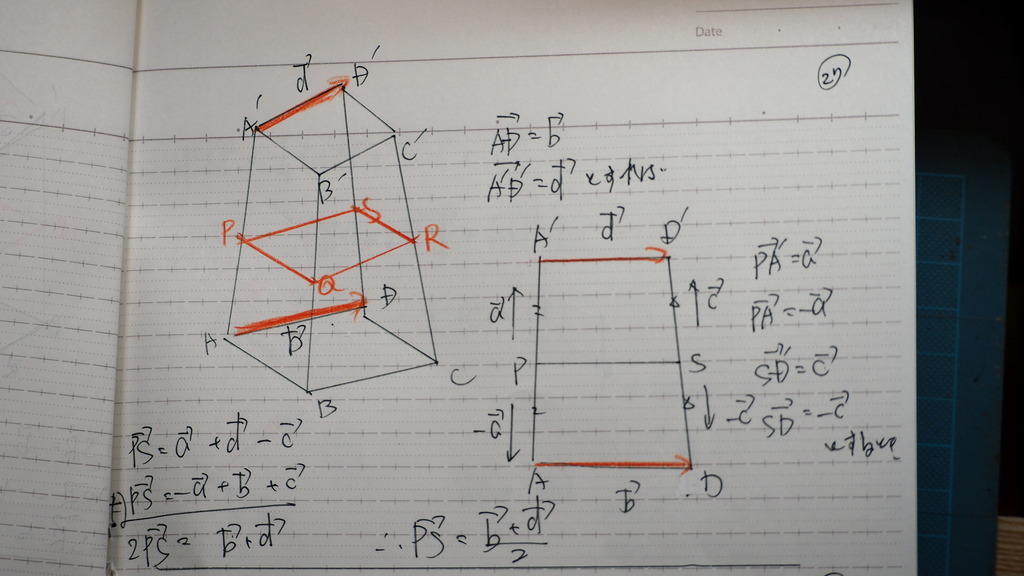
28
QRは

29
PQ と PSは
必ず 平行とは 限らない
であるから
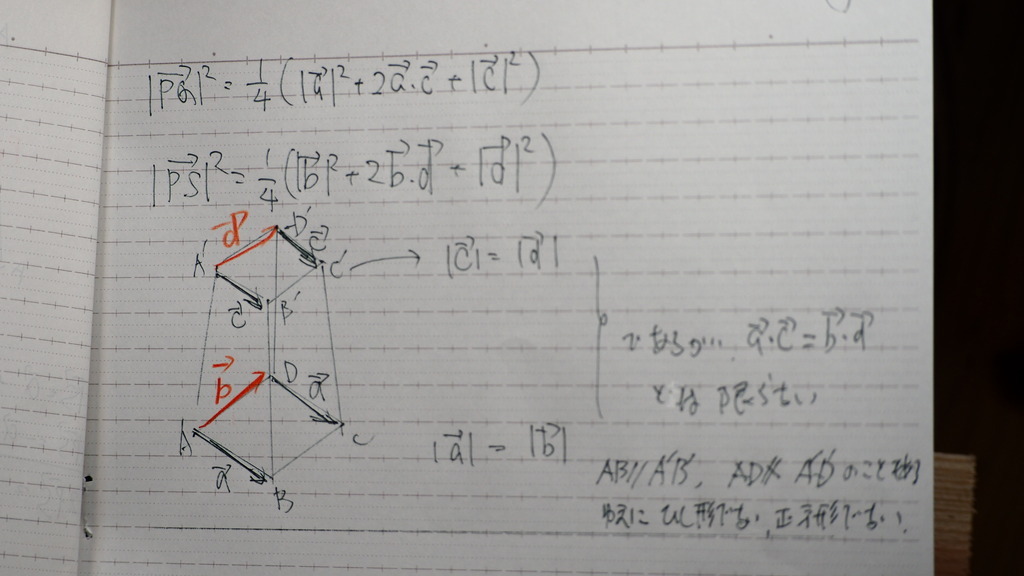
平行四辺形
お疲れ様です。
空間座標とベクトル
空間図形(1)
01
3垂線の定理と言うのがあるですが
02
問題を
図にしてくと
平面上に
2本の直線があると
Hで 交わってる
そこへ
平面ほかのPから 垂線を
下したとき
2直線に
垂線が 垂直ならば
任意の 平面上の直線に対しても
垂直であることを
示せ
03
だから
平面上に
もう1本 n と言う
任意の直線を
引くじゃナイスカ
他の2直線との 交点を
Q,R とすれば
PH 垂直 L なので
L 上のベクトル HQとも
当然 垂直
PH 垂直 mであるから
m上のベクトル HR とも
当然垂直である
ここで
出てきた ➀②の式を
引算すると
PH で くくると
04
なんと
直線 n 上の ベクトル
RQ と 垂直になってる
だから
PH 垂直 n
05
今度は
Hから 平面上の 直線に
垂線を 引いたばあい
その交点を Qとすれが
PQ 垂直 L であるを
示せ
06
PH 垂直 Lであるから
とうぜん
L 上の ベクトル QRとも
垂直である
Hから Lに垂線を引いて
Qとしたのだから
当然
HQ 垂直 QRである
今度は
この ③④式を
足すと
07
なるんですよ
08
今度は
たまに 出て来そうな 問題です
地球は 丸かった
地球を 球と考えて
A地点を 北緯0度 東経0度
B地点を 北緯45度 統計35度
としたとき
地球の中心を 0として
角AOBは 何度か
09
空間座標を
考えるでしょ
10
普段から
こういう 計算してないと
あれって思いませんか
11
だからね
コレ イメージわかるかな
12
だからね
Bの座標は こうなんですよ
13
これで
空間座標の なす角を
求めると
14
120度
15
問題
これは
ベクトルの 設定が
出来れば
半分できた
16
まず 基本的な ベクトルは
こんな感じで
AP と CQ を
こんな感じにできれば
17
2乗で 内積を
展開してくと
18
題意より
正四面体であるので
もうちょっと 簡単になる
19
こんな感じに
まとめて
20
整理して
21
これをさ
平方を 作ると
22
P,Qが それぞれ
中点の時
最初になる
23
問題
24
これはさ
中点の 連結定理で
計算したらば
PQは
25
SRは
26
ここで
平行四辺形
27
で
PSは
28
QRは
29
PQ と PSは
必ず 平行とは 限らない
であるから
平行四辺形
お疲れ様です。
22039 大人のさび落とし 空間座標とベクトル 平面図形(2)
大人のさび落とし
空間座標とベクトル
平面図形(2)
01
問題
・・・・・
外心って なんだけ
垂心って 何だっけ
重心って 何だっけ

02
外心ってのは
この場合
三角形ABCの外接円の
中心
垂心ってのは
各頂点から
対辺に 下した垂線の交点
重心てのは
そこに 糸を 付けたとしたら
つり合うところ
出ですよ
垂心であるから
例えば
AH が 対辺BCに 垂直か
調べれば
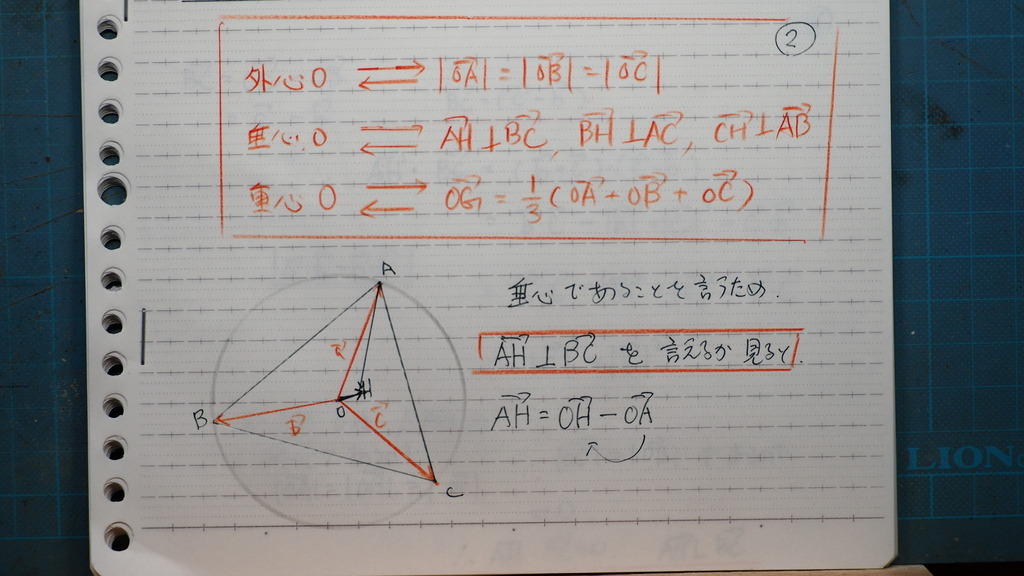
03
まず
題意よりの式
ベクトルを
設定して
AHは こうでしょ

04
BCは こうだよね
内積を
計算すると
ダメかなっと思ったとき
Oは 外心なので
OA OB OCは 等しい
なったじゃナイスカ

05
同様にですよ

06
なるでしょ

07
同様にですよ
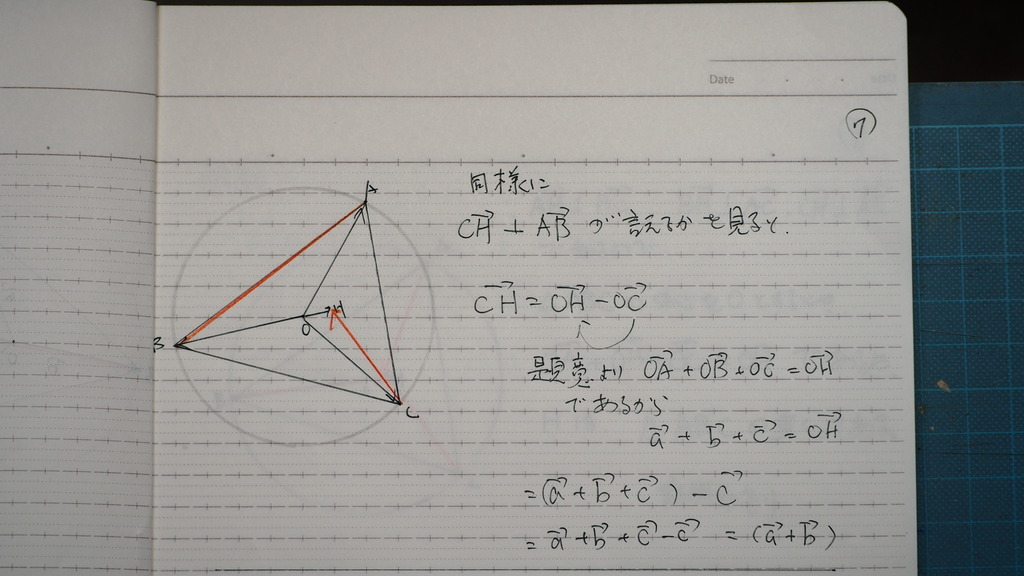
08
なりましたよ

09
だからじゃナイスカ
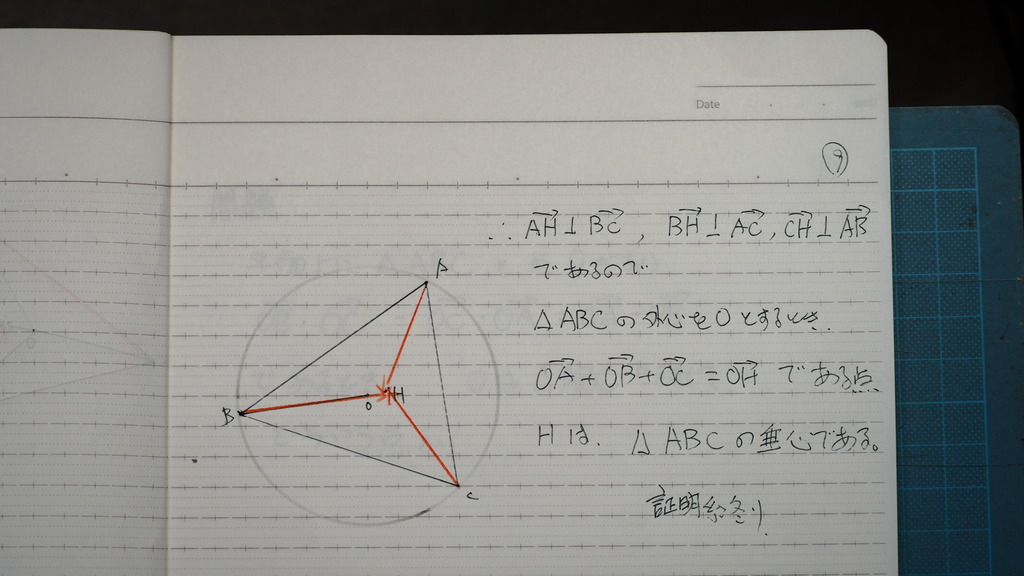
10
今度は
一直線上に
三角形の
外心 重心 垂心が
あることを 言うんですが
重心を Gとしたら
OH は OGの 3倍
Oは 三角形の 外心
ハットトリックじゃナイスカ

11
問題

12
一見難しそう なんだけど
垂直が出てきたよ
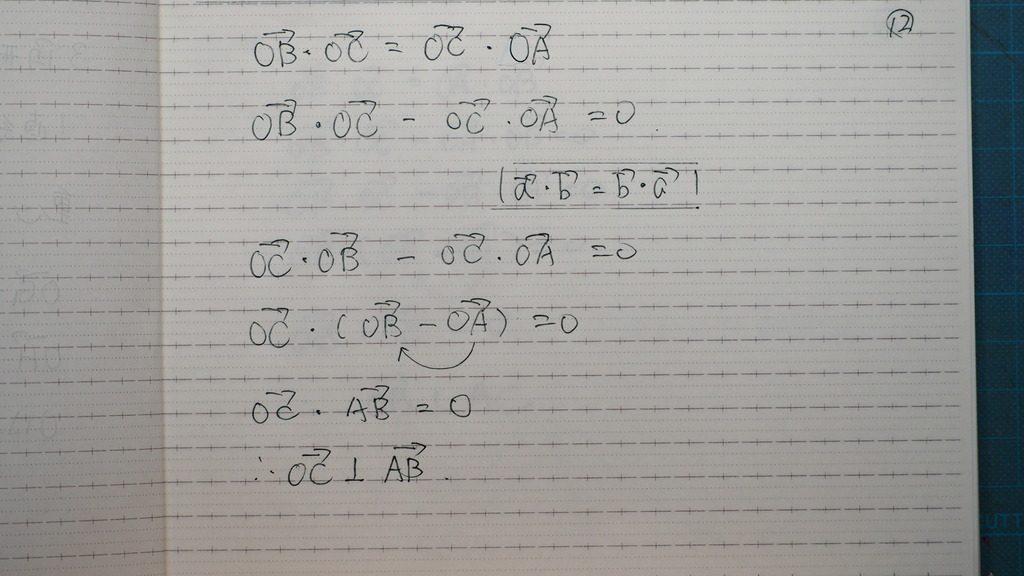
13
これも

14
これも

15
これは 垂心だよね
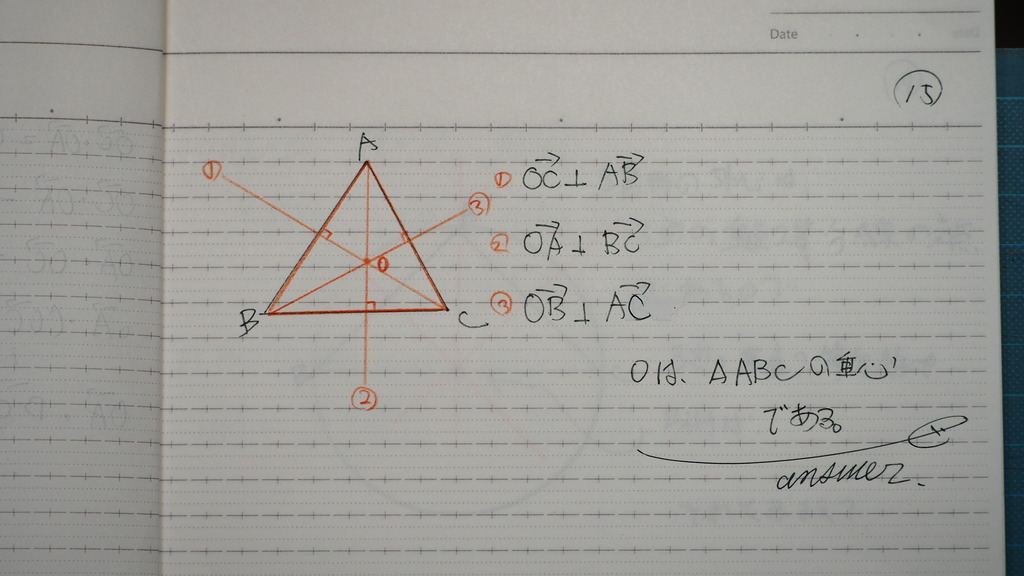
16
問題
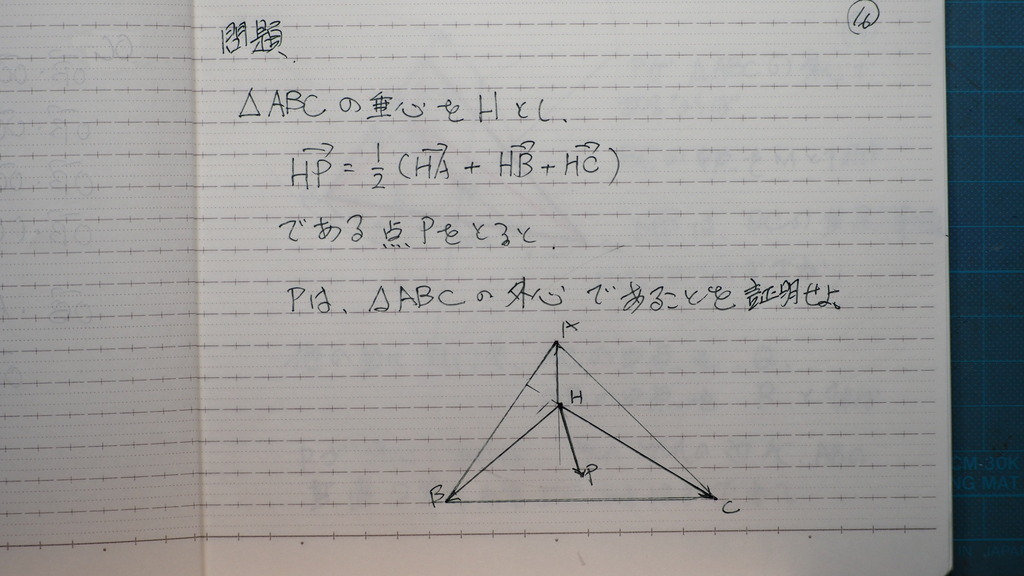
17
外心は
三辺の垂直2等分線
の 交点だから

18
P が 三角形ABCの
外心ならば
各辺の 垂直2等分線上に
Pがあるはずであるから
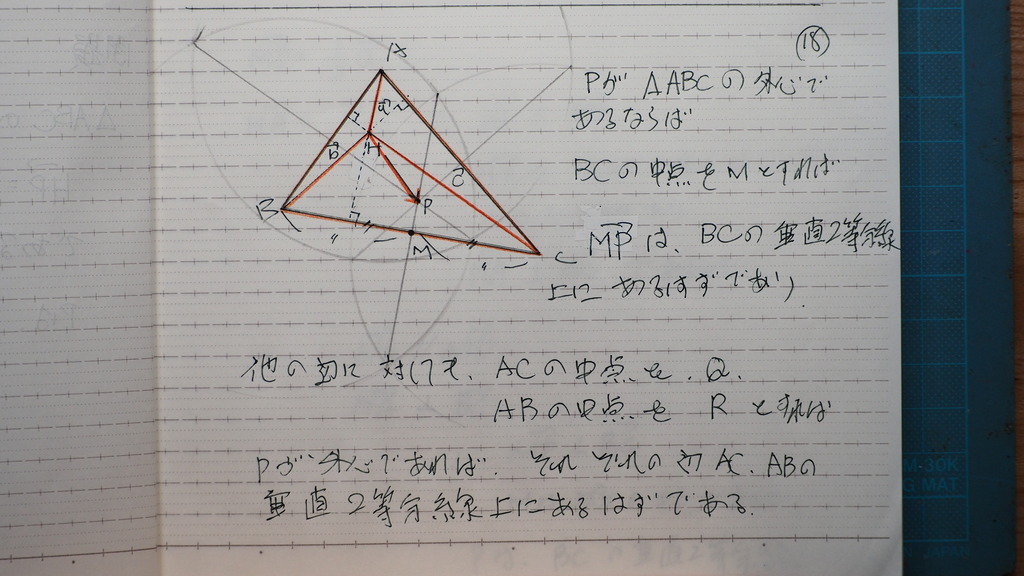
19
まず BC の 中点をMとすれば
HMは(b+c)/2
MPはHP-HM
これがさ

20
HA と 平行
Hは 垂心だから
HA と BC は 垂直
ということは
MPは HAと平行なんだから
MP垂直 BC
Mは BCの中点
なので
Pは BCの 垂直2等分線上にある

21
同様に
QPも

22
ACの 垂直2値応分線上に
Pがある

23
同様に

24
ABの垂直2等分線上にも
Pがあるので

25
Pは 外心である

26
問題

27
図にすれば
Pが 円周上を動くとき
波線を OK とおくと
Kは定点
定点と 動点の 引き算になる
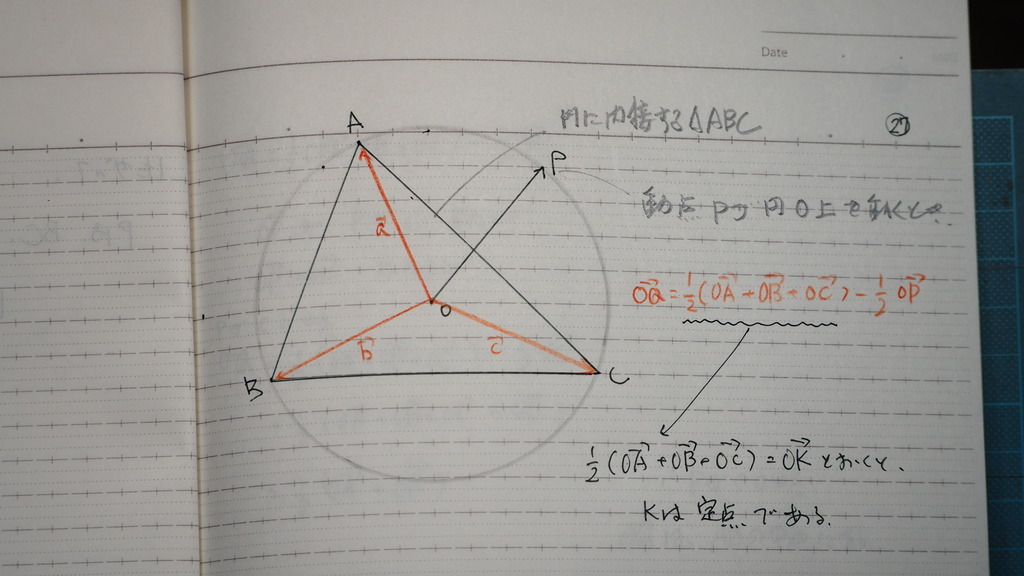
28
どうやら
Qは 円を 描くようで
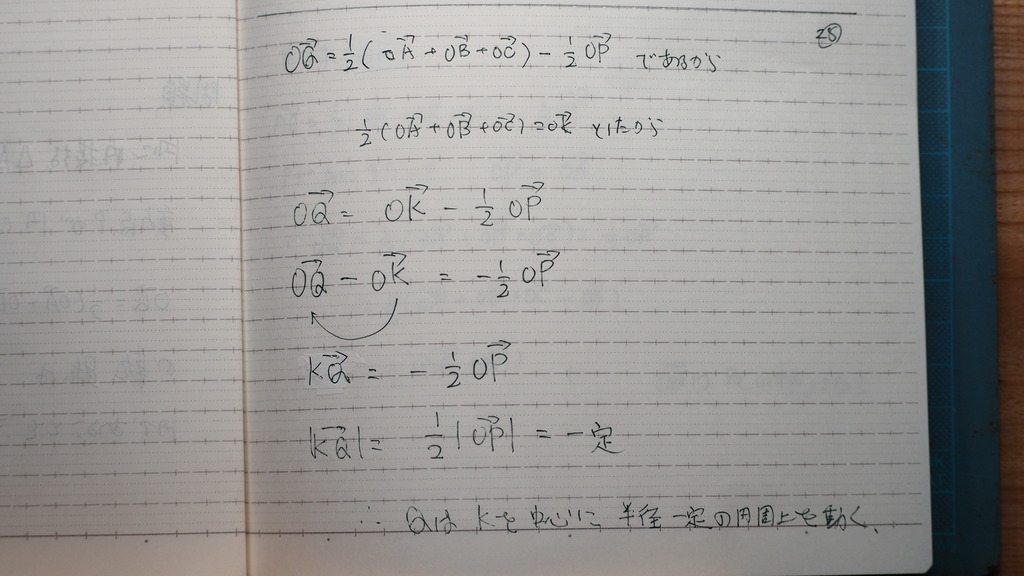
29
OPが 各頂点に来るとき
Oは 外心であるから
OPとOC
OPとOB
OPとOA
が それぞれ等しくなる
そうすると
中点を
通ってる

30
同様に
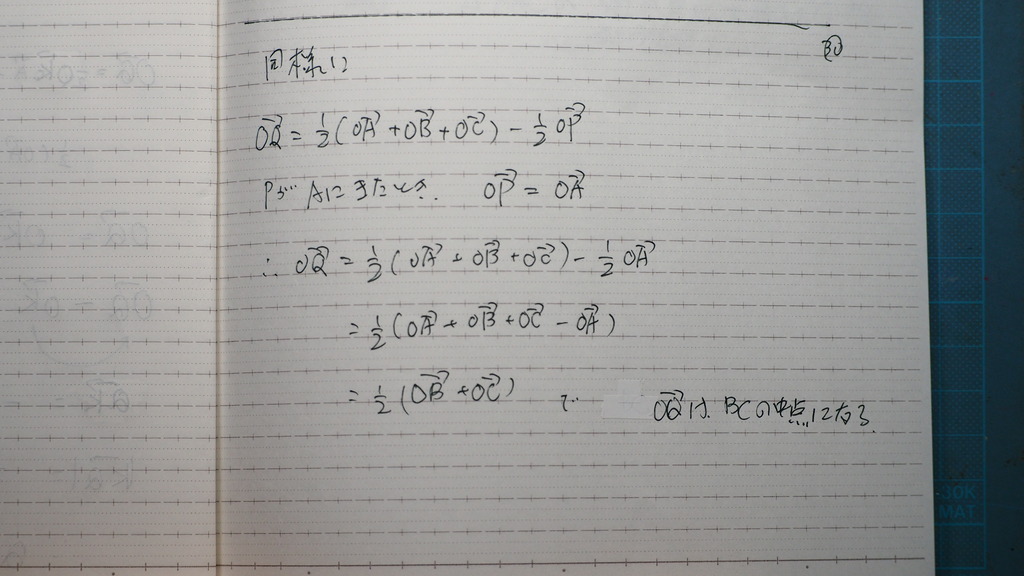
31
三角形 の 各辺の 中点を
通る円を 描く

お疲れ様です。
空間座標とベクトル
平面図形(2)
01
問題
・・・・・
外心って なんだけ
垂心って 何だっけ
重心って 何だっけ
02
外心ってのは
この場合
三角形ABCの外接円の
中心
垂心ってのは
各頂点から
対辺に 下した垂線の交点
重心てのは
そこに 糸を 付けたとしたら
つり合うところ
出ですよ
垂心であるから
例えば
AH が 対辺BCに 垂直か
調べれば
03
まず
題意よりの式
ベクトルを
設定して
AHは こうでしょ
04
BCは こうだよね
内積を
計算すると
ダメかなっと思ったとき
Oは 外心なので
OA OB OCは 等しい
なったじゃナイスカ
05
同様にですよ
06
なるでしょ
07
同様にですよ
08
なりましたよ
09
だからじゃナイスカ
10
今度は
一直線上に
三角形の
外心 重心 垂心が
あることを 言うんですが
重心を Gとしたら
OH は OGの 3倍
Oは 三角形の 外心
ハットトリックじゃナイスカ
11
問題
12
一見難しそう なんだけど
垂直が出てきたよ
13
これも
14
これも
15
これは 垂心だよね
16
問題
17
外心は
三辺の垂直2等分線
の 交点だから
18
P が 三角形ABCの
外心ならば
各辺の 垂直2等分線上に
Pがあるはずであるから
19
まず BC の 中点をMとすれば
HMは(b+c)/2
MPはHP-HM
これがさ
20
HA と 平行
Hは 垂心だから
HA と BC は 垂直
ということは
MPは HAと平行なんだから
MP垂直 BC
Mは BCの中点
なので
Pは BCの 垂直2等分線上にある
21
同様に
QPも
22
ACの 垂直2値応分線上に
Pがある
23
同様に
24
ABの垂直2等分線上にも
Pがあるので
25
Pは 外心である
26
問題
27
図にすれば
Pが 円周上を動くとき
波線を OK とおくと
Kは定点
定点と 動点の 引き算になる
28
どうやら
Qは 円を 描くようで
29
OPが 各頂点に来るとき
Oは 外心であるから
OPとOC
OPとOB
OPとOA
が それぞれ等しくなる
そうすると
中点を
通ってる
30
同様に
31
三角形 の 各辺の 中点を
通る円を 描く
お疲れ様です。