といっても今年の夏は東京も気温も上がらなかったから、あまり避暑って感じじゃなかったですけどね。まあとにかく楽しかったです! それでは気分をリフレッシュしたところで「こばとの数学基礎講座」始めましょー。
こばとの数学基礎講座
三角関数とベクトル編⑤ ピタゴラスの定理と円の方程式
さて、いつものように半径 1 の円(単位円)をぐるーりと描いてみましょー。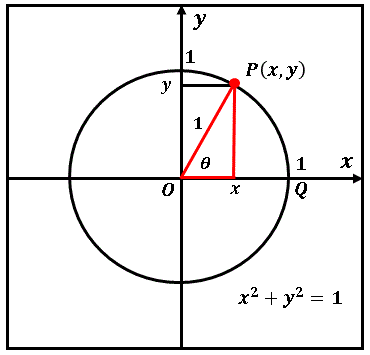
この円の上を動き回る点 (x, y) はどのような関係を満たしているのかを考えてみます。図にあるように適当な所に点 P(x, y) をとってみましょー。すると斜辺の長さが 1 で、他の 2 辺の長さが x と y の直角三角形(赤い三角形)に着目すると、かの有名な ピタゴラスの定理(三平方の定理) によって
x2 + y2 = 1
という関係があることがわかります。これが直交座標系における 円の方程式 なのです。半径 1 の円はこの関係を満たす点の集合なのです。
さて、今やりたいことは、線分 OP が x 軸となす角度 θ を使って円周上の点 (x, y) を表すことです。つまり x と y を角度 θ の関数として
x = x(θ), y = y(θ)
のように表してみたいのです。これを 三角関数 または円関数とよびます。でもこのままの記号ではちょっと紛らわしいので、x(θ) と y(θ) にあらためて
x(θ) = cosθ, y(θ) = sinθ
という名前をつけてあげることにしましょう。sin と cos はそれぞれコサイン、サインと読みますよ。さらに線分 OP の傾きを表す関数、つまり y(θ) / x(θ) を
y(θ) / x(θ) = sinθ / cosθ = tanθ
と定義します。tan はタンジェントとよびますよ。名前をつけたのはいいとして、まだこの関数がどんな性質をもつのかよくわかりませんね。とりあえず先ほどの円の方程式
x2 + y2 = 1
すなわち
cos2θ + sin2θ = 1
が成り立っているのは確かですけどね。あと円周上をぐるぐる動くところを想像してみると、第 1 象限 (x, y がともに正の領域) では、θ が大きくなるほど x(θ) = cosθ は減っていくし、逆に y(θ) = sinθ は増えていきますね(円の方程式を見てもその関係はなんとなくわかります)。今のところ、わかるのはそれぐらい。
三角関数については、ひとまずこれだけわかっていれば十分です。
次回からはベクトルについてお話しますよ。
「え? 三角関数はもうこれだけ?」と急展開に驚くかもしれないけど、ベクトルを学びながら、少しずつその正体が見えてくるようになるので、焦らないでくださいなー。それではまた次回お会いしましょー。
≫ 矢印で足し算・引き算