ボルト選手の引退レースがあんなふうに終わってしまったのは、ちょっと残念でしたねー。こばと、応援してたのになー。まあ、それはともかく今日も元気に数学しましょー。あ、そうそう、もしかすると Google Chrome をお使いの皆さんは、円周率πの表示が明朝体になっていないかもしれないかもしれません(IE なら大丈夫です)。今、Blog Cat さんが対策を検討中なのでしばらくお待ちくださいな。
こばとの数学基礎講座
三角関数とベクトル編② 度数法と弧度法を互いに変換します
前回は 弧度法 について学びました。でも今まで親しんできた度数法から弧度法に切り替えるのは、慣れるまで少し時間がかかります。そこで今回はいくつか例で、度数法と弧度法をお互いに変換する練習をしましょう。
よく使う角度の変換を覚えましょう
前回の復習ですけど、下図において弧 PQ の長さをθと定めていますよ。
もちろん変換公式もあるけど、まずは簡単な例で感覚的に変換してみましょー。アップルパイを切り分ける感じでね。パイでπを学ぶのです ...... ただの駄洒落ですよ。そんなにドン引きしないでくださいな。度数法は青、弧度法は赤色の文字で表示しますよ。まずは点 P をぐるりと1周させて円を描くと ......

これは簡単ねー。度数法では 360°、弧度法では 2π ですね。
これを次々に半分にしていきましょー。
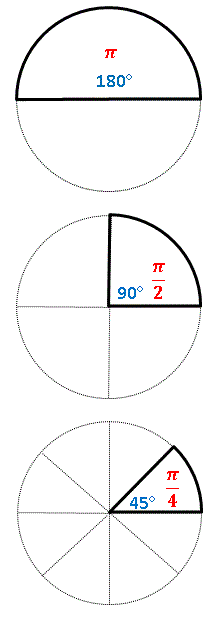
度数法では 180°, 90°, 45°となって、弧度法では π, π/2 , π/4 となります。それでは再び切り分ける前に戻しますよ。

今度は 6 等分、12 等分にしてみましょー。

度数法では 60°, 30°となって、弧度法ではπ/3 , π/6 となるのです。大体このへんまでがよく使う角度なので、図を何度か見て計算しないでもぱぱっと出てくるようにしてくださいな。
度数法と弧度法を計算で変換しましょう
でも 17°とか 55°というような中途半端な角度の場合は、さすがに計算しないと変換できません。でもπラジアン = 180° [1]
てことだけ覚えていれば、いつでもお互いを変換することができますす。[1] の両辺をπで割れば 1 ラジアンが何度なのかわかります。
1 ラジアン = 180°/π (≒ 57.296°) [2]
逆に [1] の両辺を 180°で割れば
π/180 ラジアン = 1° [3]
となります。それでは「度数法 ⇔ 弧度法」の変換を練習してみましょう。たとえば 「 2.5 ラジアンは何度かなあ」と思ったときは [2] を使って
2.5 × 180°/π= 450°/3.14 = 143.31°
というように計算することができます。「 41°は何ラジアンかなあ」と思ったときは
41π/180 = 41 × 3.14/180 = 0.72 ラジアン
と計算できますよ。関数電卓や Excel があれば、計算式を知らなくても簡単に「度数法 ⇔ 弧度法」の変換ができるけど、何回かは自分で練習したほうが感覚をつかみやすいですよ。それでは、今回はこのへんでー。次回は「負の角度」について学びますよー。
≫ 角度の符号