Excel VBA　数学実験室

こばとの数学基礎講座01　数の種類

　夏休みも近いので中高生向けの基礎編を始めます。初回なので紹介のために最新記事にアップします。夏休み後にサイドバーメニューに引っ込めますので、これまでのExcel数学を楽しみにしたいた人もご心配なく。これからも本編では「複雑な形のグラフ」を紹介していきます。

こんにちは！　KOBATOです！
　『眺めて楽しむ数学ブログ　エクセルでお手軽に数学しよう！＜基礎編＞』を担当することになりました。それにしてもやたらと長い名前のタイトルですねー。ここのブログ主さんのセンスがないんでしょうねー。面倒なので 『数学基礎講座』とでも言っておくことにします。ついでに私の名前もくっつけて『こばとの数学基礎講座』としておきましょう・・・・・・元のタイトルがほとんどなくなっちゃったね・・・・・・ま、いいか。それでは、これからよろしくお願いします！

　数学は読んで字のごとく"数"を扱う学問です。
　"数"と聞いたとき、"1, 2, 3, ・・・・・・ " というふうに頭に思い浮かべるのではないでしょうか。人によっては "0, 1, 2, 3 ・・・・・・" と 0 を含めて並べるかもしれません。上の二通りの並べ方は数学では別々の種類に分類されます。後でも説明しますが、それぞれ「自然数」、「正の整数」と呼ばれています。
　数学では「これはこういう数だよ」、「それはこういう数だよ」ときちんと決められています。いい加減な使い方をすると「ダメ！」と怒られてしまいます。そこが数学の厳しいところですね。ですから初めにしっかりと数の分類について学んでおきましょう。

　中学生の皆さんにとっては唐突かもしれませんが、「虚数」の説明から始めたいと思います。そのほうが数全体を分類しやすいのです。最初は少し不思議な感じもあるかもしれませんが、そのうちに慣れます。


という方程式があります。その意味は「同じ数同士を掛けて -1 となる数を求めなさい」ということです。難しく言うと「２乗して -1 になる数を求めなさい」という難問です。初めてこの問題を目にした人は、「え？　え？」と戸惑いながらも頭の中であれやこれやと答えを見つけ出そうとするかもしれません。でもいくら探したところで無駄な努力というものです。そんな数はないんですから。「なんだと！」と怒らないでくださいね。なければ作ればいいのです。何だかずるいようですが、数学ではそれが許されます。1 + 1 = 2 だって最初に作った「決まり事」なのですから。その決まり事が数学全体に良い影響をもたらすと皆（数学を研究する偉い人たち）が認めればそうやって「拡張」してもいいのです。
　でも数の種類が増えると、それぞれに名前をつけて区別しなければいけませんね。そこで、今まで扱ってきた普通の数を「実数」、２回掛けて −1 になる数を「虚数」と呼ぶことにします。実数と区別するために虚数は i という記号を使います。つまり、


です。これで問題は解けましたね。めでたし、めでたしです。
　まだ釈然としない気分が残るかもしれませんが、数学の勉強が進んでいくうちにこの決まり事（定義）の重要性がわかってきます。さて、この虚数ですが、２乗して −1 になる以外の計算では普通の数と同じように振る舞うように決めておきます。


というような感じで足し算、引き算、掛け算、割り算ができます。普通の数と違う所は自分自身を掛けたときに i が消滅して -1 になってしまうということです：


　では実数と虚数の足し算はどうするのでしょうか？　計算のしようがないので、1 + i とか、3 + 2i のようにそのまま足し算の記号で書いておくしかありません。このように実数と虚数を組み合わせた数 a + bi を「複素数」と呼ぶことにします。「複素数」はこれから区分する全ての種類の数を含みます。ですからあらゆる数は「これは複素数だね」と言えば、正解と言えば正解なのですけど、やっぱり物事はもう少し細かく分類しておかないと、これから色々と不便です。

　そこでまず実数を「有理数」と「無理数」とに分けます。

　「有理数」とは 1/2, 3/7 のように分数で表せる数のことです。別の言い方をすれば、1：2, 3：7 のように比で表せる数ということです。

　では無理数とは何でしょうか？
　一辺の長さが１の正方形を書いてみます。そして対角線を引きます。この対角線の長さを求めてみましょう。小学校でやる図形の問題みたいですよね。でもこれ、簡単なようでいてとっても難しいのです。もう少し先のお話の先取りになりますが、少しだけ『ピタゴラスの定理』を使ってみましょう。

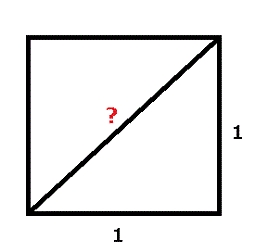
直角三角形の斜辺の長さを x, その他の２つの辺の長さを a, b とすると、


が成り立つことが知られています。今は a = b = 1ですから、とても簡単な形となって、


となりますね。つまり「２乗して 2 となる数を求めなさい」という問題になります。さきほどの虚数の場合と比べると、「何となくできそうだな」と思えますよね。ちょっと探してみましょう。1 と 2 の間にあるはずですから、x = 1.5 としてみましょうか。


ちょっと大きすぎました。少し値を小さくして x = 1.4 としてみます。


　惜しいですね！
　今度はちょっぴり小さかったようですね。なので「ちょっぴり」足して、1.41 にしてみますね。

　あと少しで正解にたどりつけそうですよ！
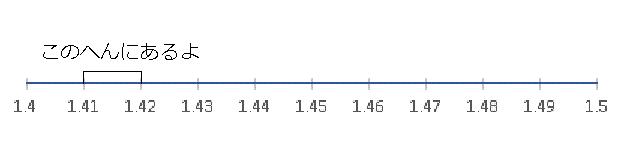
　x = 1.42 でどうでしょうか？


　ありゃ？　今度はちょっと大きくなってしまいましたね。
　それなら x = 1.415 ぐらいでしょうかね。


　・・・・・・ほぼ正解？　これでよしとしますか？　「そんなのはすっきりしない！　きっちり 2 にならないとダメ！」と思われる人がほとんどだと思います。でも実は上の方法をいくら繰り返しても決して正解は得られないのです。汗水たらして何とか頑張って続けてみると、


　という数が得られます。しかし、これを１０年続けたところで、答えに近づくことはできても、残念ながら本当の正解には辿りつけないのです。「じゃあ、これも虚数と同じで普通に存在しない数なの？」と思うかもしれませんが、虚数とは異なります。実数の中に「必ずある数」なのです。1.40 と 1.42 の間に確かに存在するはずです。図形に現れている線分なのですから。でもそれを小数の形で書くことができない数なのです。仕方なく、この「あるはずの数」を√の記号を使って √2 というふうに書くことにします。「ルート２」と読みます。これが無理数です。英語では irrational number と書きます。irrational とは「不合理な」という意味です。あるはずなのに書けないのですから、確かに不合理ですよね。数字の世界は不思議です。

　有理数に戻りましょう。これも「整数」と「分数（小数）」の２つに分けます。

　「整数」とは ・・・・・・ −3, −2, −1, 0, 1, 2, 3, ・・・・・・という数です。
　「分数」とは 1/2, 2/3, 1/5 のような数ですが、分数であっても 6/3 は約分すると 2 になってしまうので、「整数」のほうに区分けされます。つまり、より正確に言うと「約分しても整数にならない分数」ということになります。

　整数をさらに細かく分けると、「正の整数」、「負の整数」、「自然数」です。
　　正の整数：0, 1, 2, 3, ・・・・・・
　　負の整数：・・・・・・ -3, −2, −1, 0
　　自然数：1, 2, 3, ・・・・・・
　
　分数は 1/4 = 0.25 のように終わりのある「有限小数」と、1/3 = 0.333333・・・・・・というように、小数点以下の数字がいつまでも続く「循環小数」に分けられます。注意しておきたいのは、小数は「無理数」とは異なって、あるところで切れていなければ必ず"循環"するということです。しなければ無理数となってしまいます！　もう大事件です！　一見して循環していなさそうに思える小数も 0.14285714285714 ・・・・・・というように長い桁をしっかり見届ければ循環節を見つけられるでしょうし、0.2239851 のように桁が有限で終わっているはずです。

　自然数のさらなる分類は数学において特に重要な概念を含んでいます。
　自然数は「素数」と「合成数」に分けられます。
　「素数」とは１とその数自身のほかに約数をもたない数のことです。ただし、1 は除きます。具体的に書き並べてみると、2, 3, 5, 7, 11, ・・・・・・です。素数以外の数は「合成数」です。合成数は必ず素数の積で表せます。たとえば、


などです。これは中学校で習う素因数分解というものですね。素数については次回で詳しく扱う予定です。

　さて、ここでまとめの意味をかねて「実数の数直線」を見てみましょう。「実数」は複素数のすぐ下に分類される数でしたね。

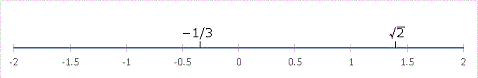
　実数というのは「上の全ての数直線を満たす数」です。もし満たさなければ、数直線は線ではなくなって、途切れ途切れになってしまいます。みっともないですよね。そんなのはとても線とはよべません。ただの切れ端です。言い換えると、整数と分数、無理数をすべて使えば数直線は完全に埋め尽くされるのです。これを少し難しい言葉で言うと、「実数は連続である」といいます。この「連続である」という概念は初等段階ではあまり気にしなくてもよいのですが、数学の勉強を進めていくと大切な概念として再登場します。頭の隅に置いておいてくださいね。
　今のところ実数の連続性に関わってくるのは、閉区間と開区間という考え方です。中学校の早い段階で不等号の使い方は勉強しますね。


という記号です。「−1 以上で 1 以下の数」です。これを閉区間といいます。別の記号を使って [a,b] と書くこともできます。なぜ閉じているというのでしょうか？　それは次の開区間を見ることでわかってきます。


これを開区間、別の記号で {−1,1} と書くのですが、とても深い意味をもっています。x は端の −1 や 1 の値をとれませんが、そこに限りなく近づくことはできます。ちょっと試してみましょう。 1 に近い数として 0.99 あたりをとってみましょう。近いですね。あと少しで端にぶつかってしまいそうな数ですね。でも 0.999 はもっと近いですよ？　0.9999 ならさらに近いです。0.999999999 ・・・・・・というように桁数を増やせばいくらでも近づくことができますね。そこに終わりがありません。こういう状態を「開いている」とよぶわけです。
　ちなみに −1 < x ≦ 1 や −1 ≦ x < 1 のように片側だけが開いていることを半開区間といい、(−1, 1], [−1, 1) のような記号で表すこともできます。

　ふう。疲れましたね。これで「数の分類」はおしまいです。表にまとめておきますね。


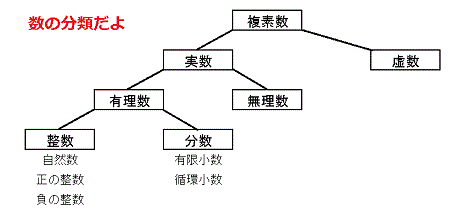
　では、こばとの数学基礎講座２＜素数＞でお会いしましょう！
　（一人で話してると疲れるね。次回は小春ちゃんでも呼ぼうかな・・・・・・話が進まなくなるかもしれないからやめとこうかな・・・・・・どうしようかな）

　おまけとして、少し不思議なお話をしますね。

とおいて、両辺を10倍します。
右辺を少し変形して、
右辺の２項目は a に等しいので置き換えますね。
となります。右辺の a を左に移項すると
ですから、両辺を 3 で割ると、
a の値を代入してみると・・・・・・
となります。「そんなばかな！」と思われるかもしれませんが、これは数学的に全く正しいのです。これが「極限値」という考え方なのです。さきほどお話した開区間において、1 に極限まで近づいた状態です。これを認めなければ、3a と 1 の間が空いてしまいます。数直線に穴が開くということです。連続ではなくなってしまい、数学は破綻します。これを正しいと認めることで、数学は「微分」という概念を獲得してさらなる飛躍を遂げたのです。