[Excel] 波の数を増やしてギザギザにします
今回は f(x) = log [1 + x + 1/x + g(x)] という関数を作って g(x) に三角関数を入れてみます。その前にまず g(x) = 0 としたときのグラフを見ておきましょう。
原点付近で + ∞ になり、極小値を作ったあと再びゆったりと + ∞ へ向かう関数です。
それでは g(x) = cosx を入れてみます。

全体的になだらかに波打つようになりました。
cosx の影響で極小値をとる x もずいぶんと右側に寄っています。
今度は g(x) = cosx + sinx としてみます。

波の数が増えてきました。g(x) = cos5x + sin2x とすると ......

振動周期が短いのでギザギザです。
[Excel] 波打ちながら二次関数的に振る舞うグラフ
三次関数を1次式を含む関数で割って、二次関数的なグラフを解析してみます。y = x 3 を x - sinx で割ってみます。定義域は 0 < x です。
予想通り波打ちながら2次関数のように振る舞うグラフが描かれました。(10, 100), (20, 400) の付近を通っていますね。しかし前回と異なり、原点付近で急増する関数ではありません。むしろ原点付近では平坦になっていますね。これは x - sinx と x 3 が均衡を保っているということを示しています。具体的に計算してみますと、
x = 0.1 : y = 1.000E-03 / 1.666E-04
x = 0.01 : y = 1.000E-06 / 1.667E-07
x = 0.001: y = 1.000E-12 / 1.667E-13
というように、急激に x を変化させても比率(およそ 1 桁違います)を保持しています。
原点付近の拡大図を見てみましょう。
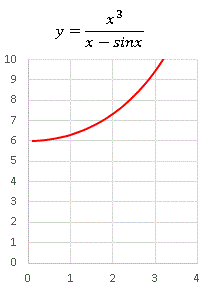
x → 0 の極限で y → 6 になることがグラフから見てとれます。不思議なことにきっちり 6 という整数です。この値はどこからくるのでしょうか? その答えは sinx の級数展開にあります。連続で微分可能な関数は x の多項式で表すことができることが知られています。 sinx の場合は、
となります。これを y に代入して分子・分母を x 3 で割ると、
という形になりますね。x → 0 の極限を取れば y → 6 が得られます。数値計算だけではデータで 6.003000786 のような値を見ることになるので、本当に正確に 6 に収束するかどうか確信することはできません。大事なところは数学の基本に立ち返るということも大切です。