問題36 数字のピラミッド [高2★★☆☆☆]
下図のような数字のピラミッドを作ります。同じ規則で下まで無限に段が続いていると考えてください。
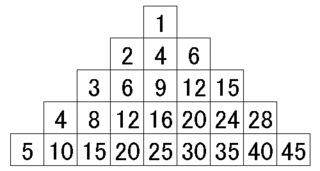
上から数えて 1 段目から p 段目にある数を全て足し合わせるといくつになりますか。
[ヒント] もちろん数列の知識を使います。見た目ほど難しくはないです。答えの式が出たらいくつかの数字で検算してみてください。
≫ [Amazon数学書籍] 若き数学者のアメリカ(新潮文庫)
解答36(等差数列の和の公式を用います)
まず上から k 段目にある数字の和 σ (k) を求めます。等差数列の和の公式は
ですから、初項 a1 と項数 n , 公差 d がわかればよいのです。 k 段目の初項は k, 項数は 2 k - 1, 公差 k となっているので、上の式に入れると
となります。念のために検算してみると、
σ(1) = 1, σ(2) = 12, σ(3) = 45
となって、確かにピラミッドの図と合っていますね。今度はこの式を 1 段目から p 段目まで足せばいいのです。念のために k2 と k3 の和の公式を確認しておきましょう。
この公式を使って頑張って計算すると
が得られます。検算してみましょう。
S(1) = σ(1) = 1
S(2) = σ(1) + σ(2) = 13
S(3) = σ(1) + σ(2) + σ(3) = 58
ちゃんと合ってますね!
PLANET 9 (第 9 惑星)は存在するでしょうか?
冥王星が惑星の仲間から外されて以来、太陽系の惑星は水金地火木土天海の 8 つとなっています。でも最近になって「海王星より遥か遠い軌道に 9 番目の惑星が存在するのでは?」と話題になっています。もちろん、仲間外れにされた冥王星のように小さな質量の惑星ではなく、「もしかすると地球の 10 倍ほどの質量があるかもしれない」と推測する人もいます。第 9 惑星の存在は「土星の軌道全体が重力の影響を受けて一定周期で変動している」などの間接的な証拠によって予言されていますが、その存在を確定するためには、やはり天体望遠鏡による発見という直接的証拠を示さなくてはなりません。
私はこの PLANET 9(第 9 惑星)に興味津々です。もし存在が確定されれば、間違いなく天文学史上に残る大発見になります。世界中の研究チームに「一番乗り」するチャンスがあります。「できれば日本の研究チーム(米と共同ですばるを使って観測を開始します)に発見してもらいたいなー」とも思ったりもしますが、でもとにかく「早く見つかってー」という気持ちのほうが大きいですね。