今は高校生の皆さんも複素平面を学んでいるようですね。
数学Ⅲの内容ですから、高校 3 年生を対象としていますが、下の補足を読んで複素平面の描き方さえ理解すれば高校 2 年生の皆さんも何とか解くことができると思います(ただし三角関数を習得している必要があります)。
問題16 複素平面に描かれる図形は? [高3★★☆☆☆]
オイラーの公式 eiθ = cosθ + isinθ を用いて次の問いに答えてください。(1) 任意の複素数を α = reiθ とおいて、xn = α の解を求めてください。
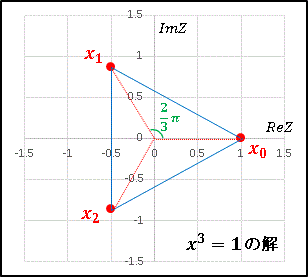
(2) x3 -1 = 0 の 3 つの解を求めて複素平面上にプロットし、3 点を結んで図形を描いてください。
≫ [Amazon書籍] 理論電磁気学
解答16(極形式に直します)
(1) αが極形式の複素数に表されているので、x も極形式にしておきます:x = ρexp(iφ)
xn = α に x, αの極形式を入れると
ρn exp(inφ) = r exp(iθ)
両辺を比較して複素数の大きさ ρ についてはすぐに
ρ = r1/n
がわかりますが、偏角については注意が必要です。
k を整数として 2kpi の任意性があることを考慮して、
nφ = iθ + 2kpi ⇔ φ = iθ/n + 2kpi/n
としなくてはなりません。結果として α = reiθ の n 乗根は
と表されます。ただし周期性から k = 0, 1, 2, ...... , n - 1 です。これ以上の k を選択しても、同じ値が繰り返されるだけです。
(2) 1 の 3 乗根を求める問題です。1 = exp(0) と表せますから、(1) で得られた式に
θ = 0, r = 1, n = 3, k = 0, 1, 2 を代入すると各 k に対応する解 xk は
x0 = exp(0) = 1
x1 = exp[i(2pi/3)]
x2 = exp[i(4pi/3)]
となります。次にこれらを複素平面上にプロットします。たとえば、
x1 = exp[i(2pi/3)] = cos[(2pi/3)] + i sin[(2pi/3)]
ですから、 実軸に cos[(2pi/3)], 虚軸に sin[(2pi/3)] をとって対応する点を描きます。こうして各点を結ぶと正三角形が描かれます。
補足 複素平面
横軸に実部(ReZ:real part)、縦軸に虚部(ImZ:imaginary part)をとり、複素数 Z = x + iy を平面上の 2 点に対応させることができます。この平面のことを複素平面(complex plane)と呼びます(下図参照)。

理系英単語⑪ 複素数
今回は複素数に関する英単語です。 complex number 複素数
real number 実数
imaginary number 虚数
imaginary unit 虚数単位
real part 実部
imaginary part 虚部
argument 偏角
Euler's formula オイラーの方程式
complex plane 複素平面
Gaussian plane 複素平面(ガウス平面)
real number 実数
imaginary number 虚数
imaginary unit 虚数単位
real part 実部
imaginary part 虚部
argument 偏角
Euler's formula オイラーの方程式
complex plane 複素平面
Gaussian plane 複素平面(ガウス平面)
Gaussian の Gauss は 18 世紀の天才数学者 Carl Friedrich Gauss のこと。もちろんガウスはこの複素平面を用いて偉大な研究実績を残したのでこの名がついているのですが、実は複素平面そのものを発見したのはノルウェーの C.ウェッセルとスイスの A. アルガンという人らしいです。なので、複素平面のことをアルガン図形と呼ぶ(私は今まで聞いたことないですけど)人もいるそうです。