Excel VBA　数学実験室

　今回は指数関数と対数関数の 3 次元バージョンを見ていきます。

折り紙を曲げる途中のようなグラフ？

　どちらも単調な関数ですから、２次元グラフが頭に入っていれば概観を予想することはできます。まずは、z = exp(x + y) という関数のグラフです：

　

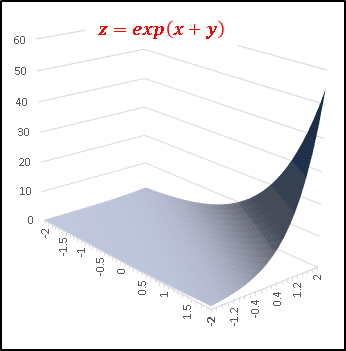
　折り紙を対角線に沿って折り曲げる途中のようなグラフですね。上図では完全に平坦な領域があるように見えますが、少し拡大して角度を変えて見てみると ……

　

　全域で傾斜する関数であることがわかります。
　ここで新しく全微分という概念を使ってみましょう。全微分は


で定義されます。 f_x と f_y は以前にも解説した x と y に関する偏微分記号です。偏微分は x と y どちらかを固定した状態における z の変化を表すだけでしたが、全微分は x, y 両方を変化させたときの z の増加傾向を知ることができます。 z = exp(x + y) について dz を計算してみると、


となります。 exp(x + y) は全領域で正ですから、x と y が共に増加する方向、すなわち dx > 0 , dy > 0 においては z は必ず増加することを示しています。

　次は xy 面内における原点からの距離 r を変数とする指数関数です：

　

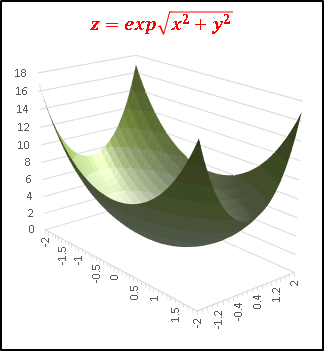
　原点から全方位に指数増加する関数ですね。
　同じように距離 r の 2 乗を変数とする対数関数です：

　

　(x, y) = (0, 0) で対数関数は定義できませんが、その付近で急速に谷底へ落ち込んでゆく関数です。x, y → ∞ において f(x, y) → −∞ ですから、この谷底は無限の深みを持っていることになります。何だか怖いですね。

　最後はおまけとして対数関数と三角関数を組み合わせてみます：

　

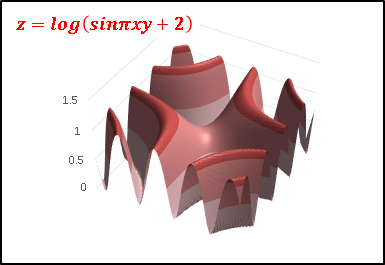
　鞍点を中心に四方へ振動が広がるやや複雑な関数です。
　log( ) の中の + 2 は定義できない点を避けるための工夫です。
　

重たくなります

　２変数グラフを扱うとデータ量が非常に多くなるので、Excel の動作が重くなります。この記事のためのグラフを描いているときは何度もフリーズしてしまいました。そのたびに再起動して少しでも軽くするための工夫をします。たとえば最後のグラフで sin(xy) とせずに sin(pi*xy) としてありますが、これは三角関数をなるべく狭い範囲で振動させて格子点を減らしたいからです。「もっとスペックの高い PC に換えれば？」と言う人もいるかもしれませんが、私はケチなので、今あるノート PC が壊れるまで使い続けたいのです。