Arctanx の導関数
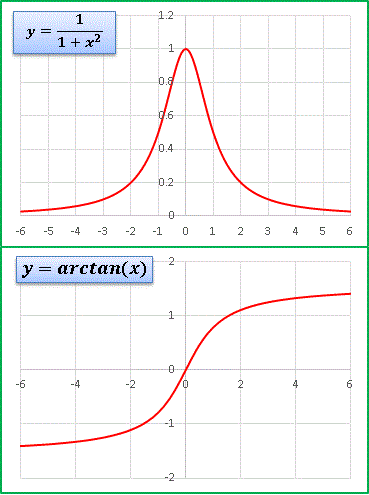
今回は次のような偶関数をベースにします。これは逆正接関数 arctan(x) の勾配を表す関数(導関数)です。
つまりこの関数を積分すると arctan(x) が得られます:
この積分はよく出てくるので丸暗記してしまっても損はありません。
arctan(x) はアークタンジェントと読み、次のような関係があります。
y = arctan(x) ⇔ x = tany
arctan(x) を tan-1(x) と書くこともあります。
[1] に x をかけてみます:
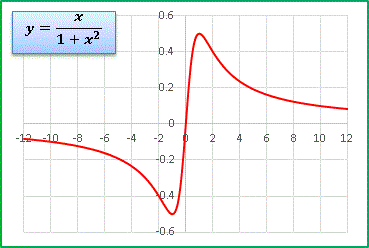
奇関数ですね。 x < 0 で負の値をとるようになります。
この関数にさらに x をかけると再び偶関数になりますが ......
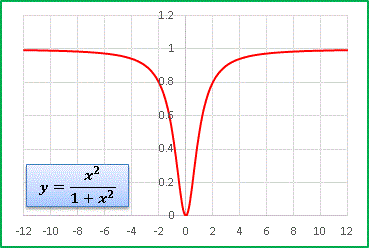
今度は原点で谷を作ります。 [1] が原点で最大値 1 をとる関数ですから、 x 2 をかけると原点近傍は y < 1 となります。漸近線は y = 1 です。次はこの関数の分子に x の項を加えてみます:
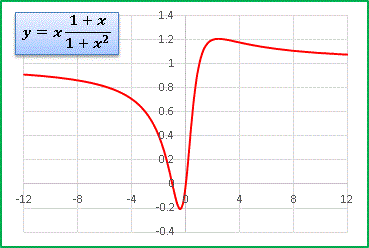
対称性は失われますが、やはり漸近線は y = 1 です。
分子・分母ともに2次式であることに変わりはないからです。
最後に [1] に sinx と xsinx をかけて奇・偶の周期関数を作ってみます:
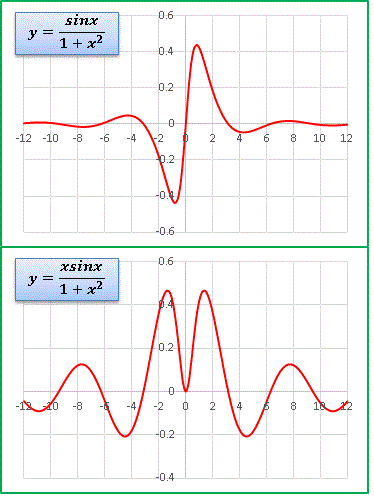
いずれも振動しながら両端(x → ± ∞)で y → 0 に収束していきます。
昔書いた小説を載せておきました
夏目漱石の『夢十夜』という作品をご存知の方も多いと思います。「こんな夢を見た ...... 」という出だしで十の夢を順に語っていくという一風変わったお話なのですが、私はこの作品をたいへんお気に入っていて、これを真似して数年前に寝ているときに見た夢を題材にした短編を何作か書いてみました。『言葉の工房あとりえこばと』の片隅にいくつか載せてあるので興味のある方は読んでみてください。好評であれば今後も少しずつ追加していきます。素材が夢ですから、とにかく不条理なお話で、展開の辻褄があっていません。そのあたりは好き嫌いが別れるところだと思います。今回は『鰐とすき焼き』という作品をお勧めしておきます。できれば正直な感想もコメントでいただきたいです(向こうのサイトでも、こちらのブログでも好きな方にコメントしてください)。「つまらん!」とか「文章が下手!」、「情景描写能力に欠ける!」などの厳しい意見も歓迎です。何しろブログで作品を発表しても、コメントがないと自身の作品の客観的な優劣がわからないのです。アマチュアなのですから、そんなこと気にせず好きにやっていればいいと言われたら、それはまあそうなのですけど、やはり他人の評価もそれなりに気になるものなのです。