[Amazon 広告] 現代三角関数論
 [内容:多重三角関数論/多重フルビッツ・ゼータ関数/絶対数学/重み付き多重ガンマ関数論/レルヒの公式/負位数/多重サイン関数/2重サイン関数/スターリング数/二重余接関数/アイゼンシュタイン級数の保型性/ガンマ因子/コンパクト・リーマン面/黒川テンソル積/イプシロン関数/反傾表現]
[内容:多重三角関数論/多重フルビッツ・ゼータ関数/絶対数学/重み付き多重ガンマ関数論/レルヒの公式/負位数/多重サイン関数/2重サイン関数/スターリング数/二重余接関数/アイゼンシュタイン級数の保型性/ガンマ因子/コンパクト・リーマン面/黒川テンソル積/イプシロン関数/反傾表現]
今回のベースとなる方程式は
x2 - y2 + 1 = 0 [1]
という双曲線です。双曲線は普通
x2 - y2 = 1 [2]
で表されますが、この式で x と y を入れ替えると [1] が得られます。つまり [2] は y 軸に関して対称ですが、 [1] は x 軸に関して対称な双曲線となっています。 [1] のグラフは下図のようになります。

① 原点付近でカーブが緩やかになります
双曲線の方程式に三角関数を組込んでみましょう。定数項の + 1 を cosx に置き換えて
x2 - y2 + cosx = 0
という方程式を作ってみると次のようなグラフが得られます。

|cosx| ≦ 1 ですから、概形にさほど大きな変化を与えませんが、原点付近ではカーブが緩やかになっています。 x と y が大きなところでは cosx の影響はほとんど無視できるので、 x2 - y2 + 1 = 0 のグラフと重なることになります(漸近線です)。
② 蛇行が目につくようになります
cos x の項を cos2x に変えてx2 - y2 + cos2x = 0
という方程式に変えてみると ......
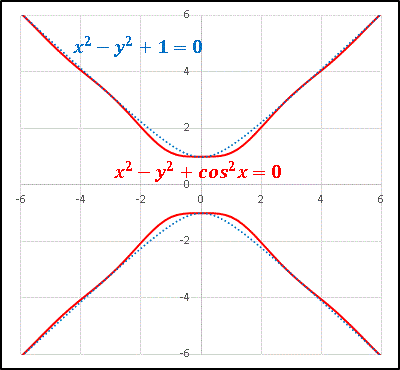
原点付近に平坦な部分が現れ、蛇行も目につくようになります。
x → ±∞ では、やはり cos2x の影響は無視できるので、 x2 - y2 + 1 = 0 が漸近線となります。
③ 双曲線的な性格は失われません
今度は少し趣を変えてx2 - (y cosx)2 + 1 = 0
という関数を作ってみます。
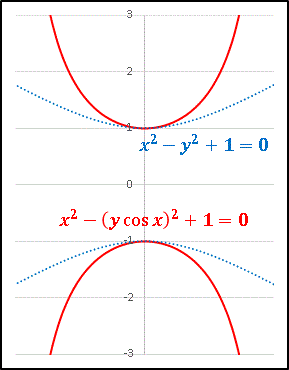
青の点線で描いた普通の双曲線よりも曲率が大きくなっていますが、やはり双曲線的な性質は失われていません。