�� n �� �� �� 0 �Ɏ������邱�Ƃ͔��ϕ��ŗL���Ȓ藝�i�Ƃ������قƂ�ǎ����̎����j�ł��B n! ����������̂Ŏ����͂ƂĂ������ł��B�O���t�ɕ`���Ă݂�Ǝ��̂悤�ɂȂ�܂��B
�@
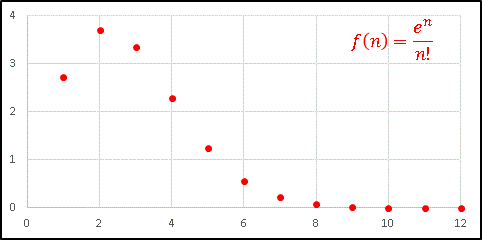
�@n = 10 ��������Ƃ�A�ق� 0 �Ɏ��������ƌ����Ă��������炢�ł��B
�w�������K���}���Ŋ���܂�
�@f(n) �������� f(x) �Ɋg������ɂ́A�K���}�� ��(x) ���g���܂��B�@��(n+1) = n! �ł�����A
�ƒ�`���܂��B������O���t�ɕ`���Ă݂�� ......
�@
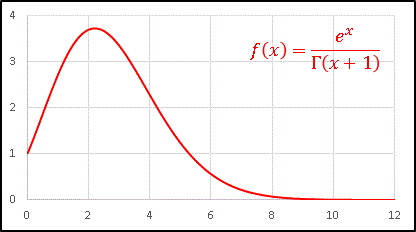
�@���̂悤�Ɋ��炩�ȋȐ��������܂��B
�@f(n) �̊e�_���A������̋Ȑ���ɏ���Ă��܂��B
�@�Ƃ���ŁA���̊��Ŏw�������� xcosx �ɕς��āA
�Ƃ������������Ă݂�� ......
�@

�@����Ȃӂ��ɂQ�̎R���ł��܂����B
�@�o���T�C�g�� �������W �ɂ܂���������肪�������Ă���̂Œ��킵�Ă݂Ă��������B���������艞���̂�����𑵂��Ă���܂��B
�@ �@