漸近線を挟んで上凸、下凸の関数が並びます
最初は a(x) = x 3 を選んで、y = x 3 + 1 / x
のグラフを描いてみます:

漸近線 x = 0 を挟んで上凸、下凸の関数が並んでいますね。
x = 0 付近では 1 / x の項が強く効くので、y ≒ 1 / x として振る舞いますが、x が少し大きくなる 1 / x の効果は減衰して y ≒ x 3 となります。具体的に計算してみると x = 3 で
a(3) = 3 3 = 27, y(3) = 3 3 + 1 / 3 = 27.333
となりますから、この段階で y と x 3 の誤差は僅かに 0.333 です。
グラフ上の青い点線は a(x) = x 3 です。x の大きいところで y と a(x) は重なってゆくことが見てとれると思います。
指数関数と重なります
次は a(x) = exp(x) です:
exp(x) は増加が早いので、この関数もすぐに exp(x) と重なります。
振動は止められて深い谷底へ落ちていきます
a(x) に三角関数を選んだらどうなるでしょうか ......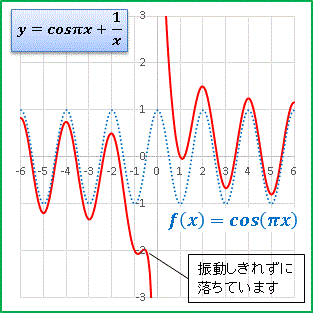
三角関数は増加関数ではないので、y と a(x) が重なるには、1 / x の減衰を待たなければなりません。 それでも a(10) = 0.1 ですから、x = 10 あたりでほぼ y = cos(pi*x) と考えて差し支えなさそうです。ちょっと面白いのは x = - 0.5 あたりでみられる cos(pi*x) と 1 / x のせめぎ合い。 cos(pi*x) は何とか頑張って値を正方向へ戻そうとするのですが、結局は 1 / x が勝って振動は止められ、深い谷底へ落ちてしまいます。
最後は a(x) としてベッセル関数 J0(x) を選択してみます:

この関数もゆっくりとではありますが、両端で J0(x) と重なります。
⇒ なんとなくの数学日記(Blog Cat は設定マニアです)