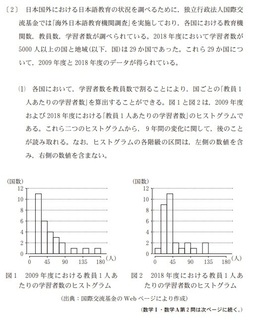
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2024�N05��06��
���wI�EA�@�ߋ���J�ɉ���y��V��z
���������A��w���w���ʃe�X�g������������Ă������Ǝv���܂��B


��
���A���������Ƃ���
�Ԏq����Ƒ��Y����́A���̓�̓������ɂ��čl���Ă���B
�@���Q�{�����{�����O
�A���Q�{�����{�����O
�@�܂��͇A�����������̌������Ƃ����B


(2)�@�����|�U�̂Ƃ��A�����R�ɂȂ�ꍇ�ɂ��̎�肤�鐔�́H
�@���Q�|�U���{�����O
�A���Q�{�����[�U���O
�Ȃ̂ŁA
���Q�|�U���{�������Q�{�����[�U
�[�U���{�����{���{�U���O


�i���|�U�j���{�i��+�U�j���O�@���̎��_�łP�������ɂȂ����̂ŁA�����
�i���{�U�j�i���|�P�j���O�@�ƂȂ�A�����|�U�܂��͂����P�ł����A
�����|�U���Ƃo���|�U�Ɠ����ɂȂ�A���̌��������Ă��܂����Ƃ���A�����U


�Ȃ̂ŁA�����P�Ōv�Z�����
�@�P�Q�|�U�{�����O
�@�����T
�A�P�Q�{���[�U���O
�@�����T
�Ƃ����킯�ŁA�����T�B���̂Ƃ��A���̉����R���ǂ����ׂĂ݂�ƁA
�@���Q�|�U���{�T���O
�@���i���|�P�j�i���|�T�j���O�@�Ȃ̂ŁA�����P�C�T
�A���Q�{�T���|�U���O
�@���i���{�U�j�i���|�P�j���O�@�Ȃ̂Ł@�����|�U�A�P
�Ȃ̂ŁA���̉��͂R�ł���A�ƂȂ�B


���̉��ɂ��ẮA�������̔��ʎ��iax�Q+bx+c�̔��ʎ��́AD=b�Q-4ac�j���g���ĉ����Ă����܂��B
�@�̔��ʎ��@�c�P���R�U�|�S��
�A�̔��ʎ��@�c�Q�����Q�{�Q�S
���ʎ������̏ꍇ�͈قȂ�Q�̎������������A�O�̏ꍇ�͏d���������܂��B�Ȃ̂ŁA
�@�O���R�U�|�S���@�ˁ@�����X
�A�O�����Q�{�Q�S
�A�̎��͂��Q�{�Q�S�Ȃ̂ŁA���ɂǂ�Ȑ����������Ă��O���傫���Ȃ邱�Ƃ���A�d���������ɂȂ�Ȃ��B
��������ƇA�̎��͂����Q�ƂȂ�̂ŁA�@�ŏd�������K�v������B
�Ȃ̂ŁA�����X�ƂȂ�܂��B
�Ȃ̂ŁA�����͂����T�A�X�ƂȂ�܂��B
���X�Ə����܂������A����Ƃ���낵�����肢�������܂��B


��
���A���������Ƃ���
�Ԏq����Ƒ��Y����́A���̓�̓������ɂ��čl���Ă���B
�@���Q�{�����{�����O
�A���Q�{�����{�����O
�@�܂��͇A�����������̌������Ƃ����B
(2)�@�����|�U�̂Ƃ��A�����R�ɂȂ�ꍇ�ɂ��̎�肤�鐔�́H
�@���Q�|�U���{�����O
�A���Q�{�����[�U���O
�Ȃ̂ŁA
���Q�|�U���{�������Q�{�����[�U
�[�U���{�����{���{�U���O
�i���|�U�j���{�i��+�U�j���O�@���̎��_�łP�������ɂȂ����̂ŁA�����
�i���{�U�j�i���|�P�j���O�@�ƂȂ�A�����|�U�܂��͂����P�ł����A
�����|�U���Ƃo���|�U�Ɠ����ɂȂ�A���̌��������Ă��܂����Ƃ���A�����U
�Ȃ̂ŁA�����P�Ōv�Z�����
�@�P�Q�|�U�{�����O
�@�����T
�A�P�Q�{���[�U���O
�@�����T
�Ƃ����킯�ŁA�����T�B���̂Ƃ��A���̉����R���ǂ����ׂĂ݂�ƁA
�@���Q�|�U���{�T���O
�@���i���|�P�j�i���|�T�j���O�@�Ȃ̂ŁA�����P�C�T
�A���Q�{�T���|�U���O
�@���i���{�U�j�i���|�P�j���O�@�Ȃ̂Ł@�����|�U�A�P
�Ȃ̂ŁA���̉��͂R�ł���A�ƂȂ�B
���̉��ɂ��ẮA�������̔��ʎ��iax�Q+bx+c�̔��ʎ��́AD=b�Q-4ac�j���g���ĉ����Ă����܂��B
�@�̔��ʎ��@�c�P���R�U�|�S��
�A�̔��ʎ��@�c�Q�����Q�{�Q�S
���ʎ������̏ꍇ�͈قȂ�Q�̎������������A�O�̏ꍇ�͏d���������܂��B�Ȃ̂ŁA
�@�O���R�U�|�S���@�ˁ@�����X
�A�O�����Q�{�Q�S
�A�̎��͂��Q�{�Q�S�Ȃ̂ŁA���ɂǂ�Ȑ����������Ă��O���傫���Ȃ邱�Ƃ���A�d���������ɂȂ�Ȃ��B
��������ƇA�̎��͂����Q�ƂȂ�̂ŁA�@�ŏd�������K�v������B
�Ȃ̂ŁA�����X�ƂȂ�܂��B
�Ȃ̂ŁA�����͂����T�A�X�ƂȂ�܂��B
���X�Ə����܂������A����Ƃ���낵�����肢�������܂��B
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
-
no image