SECH(数値)は数値の双曲線正割(hypabolic secant)を返します。
CSCH(数値)は数値の双曲線余割(hypabolic cosecant)を返します。
COTH(数値)は数値の双曲線余接(hypabolic cotangent)を返します。
sechx, cosechx, cothx は次のように定義される関数です。
SECH:sechx = 1/coshx = 2 / [exp(x) + exp(-x)]
CSCH:cosechx = 1/sinhx = 2 / [exp(x) - exp(-x)]
COTH:cothx = coshx/sinhx = [exp(2x) + 1] / [exp(2x) - 1]
sechx は実数全域で定義されますが、 cosechx と cothx は x = 0 のときに分母が 0 となってしまうので、CSCH(0) と COTH(0) は "#DIV/0!" というエラー表示を返します。「 0 で割っていますよ!」という警告です。グラフを描くときはデータから必ず x = 0 を取り除いておかなければなりません。オートフィルで入力されているときは忘れがちなので注意が必要です。
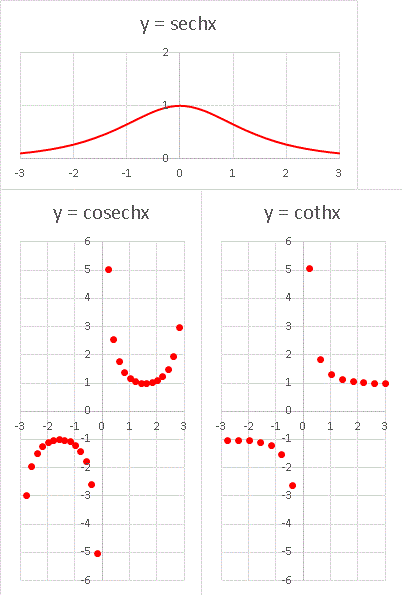
下に y = sechx, y = cosechx, y = cothx のグラフをのせておきます。
y = sechx は x = 0 で極大値をとり、x → ±∞ で 0 に収束します。
y = cosechx はやや複雑な関数です。
x → +0 で +∞ に、x → -0 で -∞ に発散します。
また、x → +∞ で +∞ に発散し、x → -∞ で -∞ に発散します。
y = cothx は x → +0 で +∞ に、x → -0 で -∞ に発散します。
x → ±∞ で 1 に収束します。
数学ブログを応援してください。