漸近線で分割される関数
高校数学では次のような関数のグラフを描く問題をよく目にします:分母を因数分解すると
となりますから、この関数は x = ±1 で定義できません。
実際にグラフを描いてみると ......
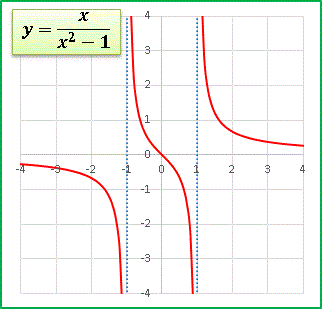
x = ±1 は漸近線です:
x → 1 + 0 (1 に x 軸右側から近づく)とき + ∞
x → 1 - 0 (1 に x 軸左側から近づく)とき - ∞
x → - 1 + 0 ( - 1 に x 軸右側から近づく)とき + ∞
x → - 1 - 0 ( - 1 に x 軸左側から近づく)とき - ∞
このように、分母が x の多項式で分母 = 0 とおいたときに2つの解を持てば、y = f(x) はグラフは2つの y 軸に平行な漸近線によって3つの領域に分割されます。もう1つ例を見てみましょう:
先程と同じように分母を因数分解すると
となるので、この関数は x = - 2 と x = 3 という2つの漸近線によって領域が分けられます。
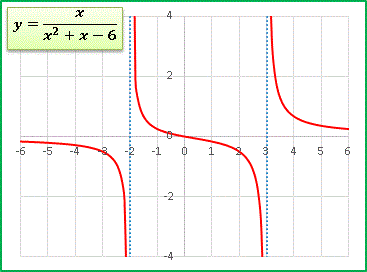
このタイプの関数は、分母 = 0 の解が得られるなら、増減表を書かなくてもグラフの概形を描くことができます。 y 軸に平行な漸近線を挟んで ±∞ のどちらに発散するかは次のように判定します。たとえば上の例で x = 3 の右側を調べたいのなら、x = 3 + εとおいて(ε はとても小さな正数です)、
分母 = (3 + ε) 2 + x + ε - 6 = ε 2 + 7ε + 2 > 0
となるので + ∞ に発散することがわかります。実際には分母をひと目みて暗算でぱっと出てくるぐらいに訓練しておきましょう。もちろん試験の答案では増減表を書かなくてはいけませんが、上の方法で先にグラフを描いてしまっておけばミスが少なくなります。
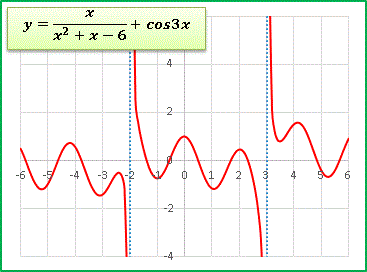
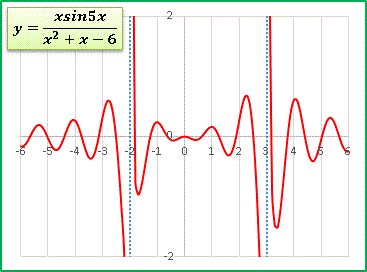
補足しておくと、今回の例では1次関数を2次関数で割っているわけですから、 x = ±∞ においては y ≒ 1 / x のように振る舞います。したがって両端では y → ± 0 に収束します。符号については、そのグラフの存在領域の境界となる漸近線における発散の符号と一致します。上のグラフで説明すると、 x → 3 + 0 で y → + ∞ でしたから、x → + ∞ で y → + 0 となります。最後におまけです。三角関数を掛けたり加えたりすると、各領域ごとに振動する関数になります:
滝野川を散策してみました
昨日は(東京都)北区滝野川6丁目と7丁目を散歩しました。『こばとちゃんワールド』の滝野川小夜子さんが住んでいるあたりです。「小春ちゃんは自転車でこの道を通って小夜子さんの家に遊びに行くんだな」とか、「こばとちゃんの飛行速度は人が歩くより早いし坂道も関係ないね」などと思いを巡らせながら作中世界と現実世界の感覚の摺り合わせをするわけです。つい先日も『こばとの英語ノート』でお花見の話を書きましたが、もちろん事前にさくら公園まで足を運びました。のんびりと花見客の脇を通り過ぎながら辺りを眺めまわして「沙希ちゃんたちはこのへんの場所に陣取るかな ......」というようなことをやっていました(ついでにお花見も楽しみましたよ)。そういう地味な散策を繰り返していると、不思議と作品を書くときの筆の運び(キーボードを打つ速度)がスムーズになります。頭ばかりで考えるよりも五感をフルに使ったほうが頭のはたらきをよくする気がします。もう若くもないので、健康のためにもなるべく外に出て歩くことを心がけたいです。