�@[Ctrl] + [+]�@�Z���̑}���@�@[Ctrl] + [-]�@�Z���̍폜
[1]sin(mx)cos(nx) �̐ϕ�
�@�L���Ȑϕ������̂P��
�Ƃ������̂�����܂��ˁBm, n �͔C�ӂ̐����ł��B
(m, n) = (1, 1) �̏ꍇ�̔�ϕ�����}�����Ă݂܂��F
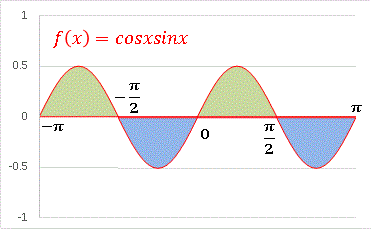
�@�}���疾�炩�Ȃ悤�ɁA��̌����̈Ӗ��́A�|pi < x < pi �͈̔͂ɂ����āA�ΐF�̕����i���̖ʐρj�ƐF�̕����i���̖ʐρj���������Ƃ��Ӗ����Ă��܂��B (m, n) = (1, 2), (2, 1), (1, 3) �̏ꍇ���܂Ƃ߂Č��Ă݂܂��傤�B

�@(m, n) ���傫���Ȃ�قNJ��̌`�͕��G�ɂȂ�܂����A�ǂ̂悤�ȏꍇ�ł��̖ʐςƐ̖ʐς͕K�����E���܂��B����� cosx �� sinx ���i���������x�N�g���̂悤�Ɂj�u�������Ă���v�ƕ\�����܂��B���͊��Ƃ����̂́A����������Ԃ̃x�N�g���Ȃ̂ł��B���̐ϕ��̓x�N�g���̓��ςɑΉ����Ă��܂��F
�@�ϕ����� 0�i���������j�@�́@���ς� 0�i�x�N�g���������j
�@��ʉ������c�_�͏�������̂ł����A���̃u���O�ł͋�̓I�ŖڂɌ����邩�����Łu���K�������n�v��������Ă����܂��B���w�V�́u�ϕ��v���K�����Ă���A�₳�������e���Ǝv���܂��B
[2]sin(mx)sin(nx) �̐ϕ�
�Ƃ����ϕ������������܂��B�ϕ��l�� pi �Ŋ����Ă��邱�Ƃɒ��ӂ��Ă��������Bm �� n �̏ꍇ���猩�Ă����܂��傤�B (m, n) = (1, 2), (2, 3) �Ƃ����ꍇ�̔�ϕ�����`���Ă݂܂��F
�@

�@�ϕ��l�� 0 �Ȃ̂ō��̂Ƃ���K�v�͂Ȃ��̂ł����A����̋L�q�Ƃ̓��ꐫ���l���āA��ϕ�����
�@�Ƃ����悤�� ��pi �Ŋ������������̐ςƍl���Ă��������B[�|pi, pi] �͈̔͂Őϕ��� 0 �ɂȂ�Ƃ������ƁA����������� sinx / ��pi �� sin2x / ��pi ����������Ƃ������Ƃ́A�̖ʐςƐ̖ʐς��������A���E����Ƃ������Ƃł��B�u������������v�Ƃ����\���ɂ́A�Ȃ��Ȃ����o������߂Ȃ���������܂��A���̂Ƃ���͂��̃O���t�̃C���[�W�ƃZ�b�g�œ��̕Ћ��ɒu���Ă����Ă��������B����ȍ~�ɂ������������ڂ������b���܂��B
�@���� m = n �̏ꍇ�A�܂�ϕ����l�������A�Q�̊����������Ȃ��ꍇ�ł��B (m, n) = (1, 1), (2, 2), (3, 3) �̂Ƃ��̔�ϕ�������ׂ܂��F
�@
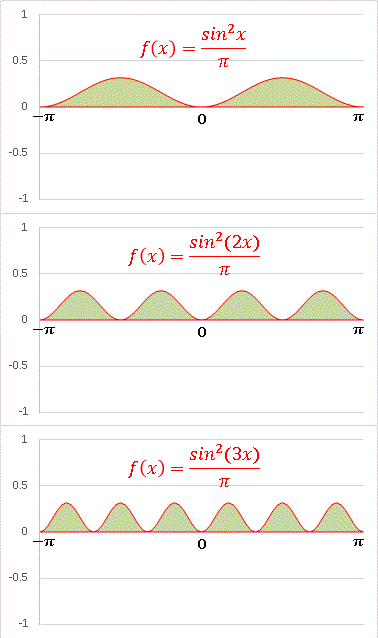
�@�������� 2 �悵�Ă���̂ŁA�S�̈�� f(x) �� 0 �ł��B�����́u m, n �̑I�ѕ��Ɋւ�炸�K���ϕ��l�� 1 �ƂȂ�܂���v�ƌ����Ă���̂ł�����A���̂R���O���t�̗ΐF�̖ʐς͑S�ē������Ƃ������ƂɂȂ�܂��Bm = n = 1 �ł������Ƃ��̓�̑傫�ȎR���A(m, n) ���傫���Ȃ�ɂ�āA�ǂ�ǂ��ȎR�ɕ��Ă����܂��B m = n = 11 �̏ꍇ�����Ă݂܂��傤�B
�@
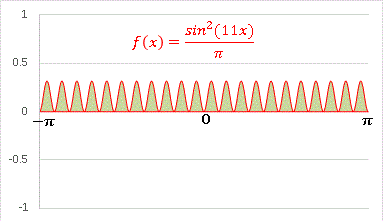
�@�ƂĂ������ȎR�i�Ƃ������u���ȁH�j�����炸��ƕ���ł��܂��ˁB������S�đ������킹�Ėʐς� 1 �ƂȂ�܂��B
[3]cos(mx)cos(nx) �̐ϕ�
�Ƃ����������O���t�Ŋm�F���Ă݂܂��B��mn �́Am = n �̂Ƃ������l 1 �������A����ȊO�� 0 �Ƃ����L���ł��Bm = n = 0 �̏ꍇ�́A��ϕ������萔 1 �ł�����A���ɈӖ��͂���܂���B�ϕ��v�Z���Č����ʂ�ɒl�� 2 �ɂȂ邱�Ƃ��m�F���Ă����Ă��������B m = n = 1 �̏ꍇ�����Ă݂܂��F
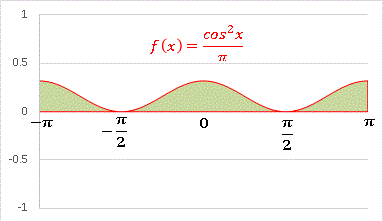
�@������O�ł����A���������m�̐ς͌����Ē������܂���B�x�N�g���ł����Ƃ���́u�݂��ɕ��s�ł���v�Ƃ�����Ԃł��B�̕�����S�������Ɩʐς� 1 �ƂȂ�܂��B
�@���� (m, n) = (1, 2) �̏ꍇ��`���Ă݂�ƁE�E�E�E�E�E
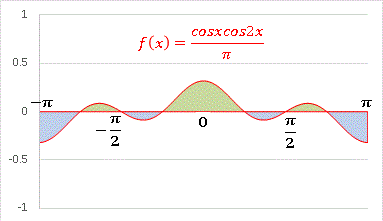
�@�Ɛ̖ʐς͑��E����� 0 �ƂȂ�܂��B�܂� cosx / ��pi �� cos2x / ��pi �́u�݂��ɒ������āv���܂��B
�O�p���̐��K�����n
�@����܂łɈ������R�̌������܂Ƃ߂�ƁF
�@cos ���m�̐ς� m = n = 0 �̂Ƃ��͔�ϕ������萔�ƂȂ�̂ŁA�P���� �� = c�i�萔�j�Ƃ����`�̊���������܂����Ac�Ecosx �� c�Esinx �� [-pi,pi] �Őϕ������ 0 �ɂȂ�̂ŁAc �� cosx, c �� sinx �͒������Ă��܂��B��̌��������Ȃ��玟�̂悤�ȏW���������Ă݂܂��F
�@�W�����̓K���Ȋ����Q�Ƃ��Ă݂āA�݂��ɒ������Ă��邱�Ƃ��m�F���Ă��������B
�@���̏W�����u�������n�v�ł���Ƃ������ƂɂȂ�܂��B
�@�W�����̂��ꂼ��̊��� 2 ���ϕ������l�� 1 �ɂȂ邱�Ƃ��m���߂Ă݂Ă��������B
�@���̏�������������Ă���A�W���́u���K�������n�v�ł���Ƃ����܂��B
�@����ɂ��Ă��A���K�������n�����̂͌��\��Ԃ�������܂��ˁB�킴�킴����Ȗʓ|�Ȃ��Ƃ�����̂́A�u�C�ӂ̊������`�œW�J����v�Ƃ������p�I�ȗ��R�̑��Ɂu���R�E�̐������L�q��������������̉����̂��̂������n���Ȃ��Ă���v���Ƃ���������ł��B���Ƃ��A�ʎq�͊w�Ő��f���q�̐U�镑�����L�q���邽�߂Ƀ��Q�[���������Ƃ����������n���K�v�ƂȂ�܂��B�u�Ȃ��K�v�Ȃ́H�v�Ɩ���Ă��A�u���R�E�������Ȃ��Ă��邩��v�Ƃ��������悤������܂���E�E�E�E�E�E�B���̂�����̂��Ƃ́A������T�C�h�o�[�ɕʂ̃R�[�i�[��݂��āA���������[���Ƃ���܂ł��b�������Ǝv���܂��B
�@�Q�̊����u�������Ă��邩�ǂ����v�Ƃ������Ƃ�ϕ����Ċm�F����̂͌��\�d�J���ł����AExcel ���g���ƁA����������邱�Ƃ��ł��܂��B���Ƃ��Ώ�̌����ł� (m, n) �͐����Ɍ����Ă��܂������A (m, n) = (1/2, 1/2) �Ƃ��āAcos(x/2) �� sin(x/2) �͒������Ă���ł��傤���H Excel �ł������Ɗm���߂Ă݂܂��傤�B
�@

�@�����̖ʐς͑��E����Ă��܂��B���炩�ɒ������Ă��܂��ˁB
�@���K�������n�����邱�Ƃ��ł���͎̂O�p�������Ɍ���܂���B
�@���͂������ʂ� n ��������H�v���Đ��K�������n�����肾�����Ƃ��ł��܂��B�O�p���ɔ�ׂ�Ƌc�_�̍ו��͂��Ȃ����̂ŏȂ��܂����A����́u�����̊��͒������Ă��܂���v�Ƃ����O��ŁA�������̒��𑽍����̃O���t���Љ�Ă����\��ł��B����͔�r�I�ȒP�ȃ`�F�r�V�F�t�������������\��ł��B
�@�]�͂̂���l�͉��̈�ʘ_���ǂ�ł����Ă��������B
�y�t�^�z���K�������n�̈�ʘ_
�@�� y = f(x) ����� [a,b] �ŁA
f = (f(x1), f(x2), f(x3), �E�E�E�E�E�E ,f(xn))
�Ƃ����悤�� xn �̓_�ŕ\�����Ƃɂ��܂��B n ���L���ł����Ă��A���̂悤�ɂ�����x���̌`��\�����邱�Ƃ͂ł��܂��ˁB

�@�܂�A�����u n �����x�N�g���`���ŕ\�������v�Ƃ������ƂɂȂ�܂��B
�@������ n �� �� �Ƃ���ƁAf(x) �Ɋւ��銮�S�ȏ������͂��ł��B
�@�Q�� n �����x�N�g�� a, b �̓��ρF
a�Eb = a1�Eb1 + a2�Eb2 + �E�E�E�E�E�E + an�Ebn
�ɑΉ�����`�ŁA�� f �� g �̓��ς�
�̂悤�ɐϕ��̌`�Œ�`���܂��B f ���m�̓��ς�
�ƂȂ�A���̕����� |f| �̓x�N�g���ł����Ƃ���̑傫���ɑ������A������� [a, b] �łǂꂮ�炢�̑傫�����Ƃ����ڈ��ɂȂ�܂��Ba�Eb = 0 �̂Ƃ��A�x�N�g�� a, b�͒������܂����A����ɑΉ�����
(f, g) = 0
�̂Ƃ��A�� f(x) �� g(x) �͒�������ƒ�`���܂��B�����ŁA
��1, ��2, �E�E�E�E�E�E ��n
�Ƃ����悤�� n �̊��̏W�����l���܂��B�W�����̑S�Ă̊��ɂ���
|��k| = 1
�ƂȂ�悤�ɓK���Ȓ萔�Ŋ����ċK�i�����Ă����܂��B
�����ďW��������C�ӂőI�Q�̊��ɂ��āA
(��m, ��n) = ��mn
�����藧�Ȃ�A�W���o��k�p�����K�������n�ł���ƒ�`���܂��B
�@
���ƂȂ��̐��w���L�@
�@���N�O�ɁA�|�e�g�T���_�ɃE�X�^�[�\�[�X��������ƁA�ƂĂ������������ƂɋC�Â��܂����B����ȗ��A�|�e�g�T���_�ɂ͕K���\�[�X�������ĐH�ׂ邱�Ƃɂ��Ă��܂��B�s�̂̂��͖̂����Z���̂ŁA���Ɛ��̔����ō�����T���_�ɂł��B�����������܂�܂��B�u�{�����ȁ[�v�Ƌ^���l�͂P�x���������������B�u����قǂł��Ȃ��������v�ƌ����Ă��ӔC�͎��Ă܂��ǁE�E�E�E�E�E�B���ƂȂ��̐��w���L�A
�@�����̃R�R�A�p�E�_�[�i�ł���o���z�[�e���j���J�b�v�ɓ���܂��B�����ď��ʂ̂����i�ł��邾�����ʂł��j�𒍂��ŃX�v�[���ł��������ėn�����܂��B�����ɂȂ�܂ő҂��܂��B������o�j���A�C�X�N���[���ɂ����āA�u�R�R�A�C�X�v�̏o���オ��ł��B�u�I�I�I�v�Ɗ�������قǂ̔��������ł��B�R�R�A�̋�݂ƃA�C�X�̊Â����قǂ悭���a���āu��l�̖��v�ɂȂ�܂��B���ЂP�x���������������B���ƂȂ��̐��w���L�B
�@�ߏ��̃��[�������Łu���k���[�����v�i���k�����̂����������[�����ł��j�Ƃ������̂����߂ĐH���Ă݂��Ƃ���A�u���̒��ɁA����Ȏ|�����̂��������̂��[�I�v�Ɗ������āA���䖲���ŕ��炰�܂����B�M���[�U�Ƃ��т��Z�b�g�ł��Ă��܂����B�喞���ł��B���ƂȂ��̐��w���L�C
�@���̃u���O�̃T�C�h�o�[�ɂ���J�e�S�����Łu���K������ "�n"�v�ƂȂ�ׂ��Ƃ��낪�A�u���K������ "�`"�v�ƂȂ��Ă��邱�ƂɋC�Â��܂����B�����n�����Ƃ������Ƃ��ꂻ���Ȃ̂ōQ�ĂĒ����Ă����܂����B�ӂ��B��Ȃ��Ă悩�����I�@ �@