Excel VBA　数学実験室

sinx , cosx を 3 乗します

　y = sin³ x という式は三角関数を勉強していれば普通に目にしますが、さてどんなグラフと聞かれてもぴんとこないと思います。私も周期関数だから、y = sin x と似たような形だろうなと適当なことを考えておりました。そこで、エクセル使って描いてみると・・・・・・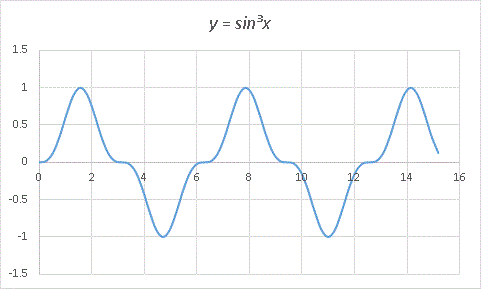

　

　似ているといえば、似ていなくもないですが、途中に平坦な部分が出現しています。この平坦な部分は x = 0, π, 2π, ・・・・・・、つまりsinx が 0 になる近傍であり、 3 乗することで値の小さなところが押しつぶされているのです。逆に山や谷のある所、つまり sinx が 1 或いは−1 になる付近では、1, −1 に近い数を３乗したところで、それはやはりおよそ 1 , −1ですから、普通の y = sin x と相似しているのだと思います。

cos³x のグラフも一応載せておきます。

　

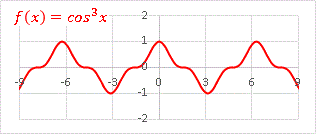
これはもちろん sin³x を平行移動させたグラフですね。

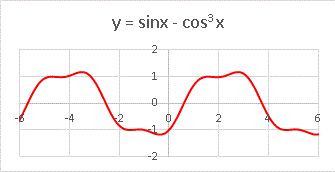
次は y = sin³ x - cos³ x という少し複雑な関数です。

　

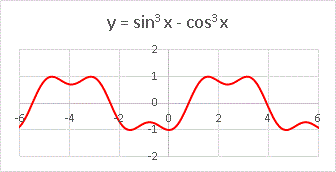
　これは面白いグラフですね。小さな凹みのある山が周期的に現れます。
　この関数を少しいじってみましょう。

　sin³ x の部分を sin² x に変えてみますと・・・・・・

　

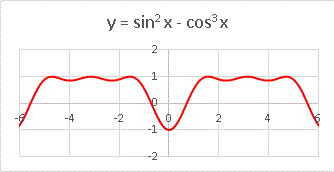
　山の凹みが２つになりましたね！　ここからさらに sin² x の部分を sinx としてみると・・・・・・

　

　山が傾きました。

　cos³x に sin^mx を加えてみます。まずは m = 1, 2, 3, ・・・・・・とした場合：

　

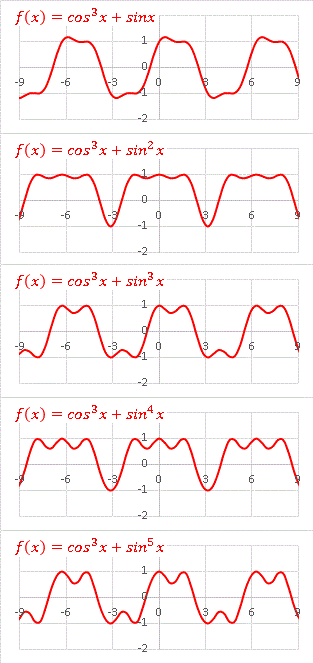
　m が偶数同士、奇数同士のグラフはそれぞれはよく似た形をしています。
　m が有理数の場合を見てみましょう。sinx が負になる領域では定義できないので、-pi < x < pi の範囲に限定します。 m = 0.5, 1.5, 2.5 でグラフを描いてみます：

　

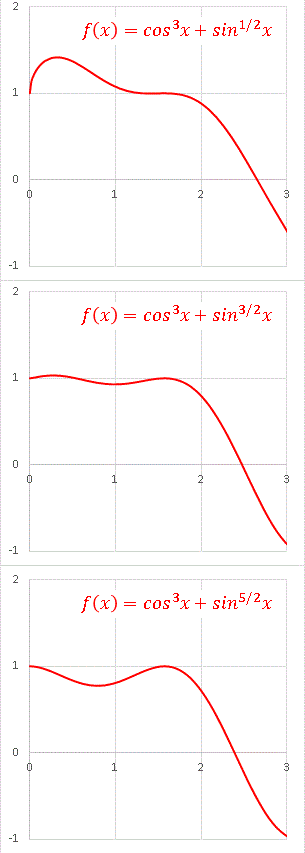
　こんな感じになります。m = 3.5, 4.5 , ・・・・・・と増やしていくと山と谷の形がよりシャープになっていきます。

　押していただけると有り難いです。
　
　

Excel 数学関数辞典をご利用ください

　エクセルでグラフを描くときの参考になると思います。PC の人は右サイドバーから、スマホの人は記事下のメニューから選択できます。COMBINE（組合せ）関数をグラフでプロットするなど、あまり他では見ないような説明を心がけています。