今年最初の記事は、去年も予告していたように トロコイド(trochoid) を扱います。トロコイド・・・・・・あまり馴染みのない響きですね。しかし名前の響きほど内容は難しくないので、あまり構えずに肩の力を抜いてグラフを眺めてください。少し長くなりますが、トロコイド、内トロコイド、外トロコイドを順に説明していきます。
トロコイド(Trochoid)
円(動円)を直線にそってすべらないように転がしたとき、その円の内部または外部の定点が描く曲線を トロコイド と呼びます。ちなみに漢字で書くと余擺線(よはいせん)ですが、こんな字を見ると必要以上に難しそうな気になるのでやっぱりトロコイドと呼ぶことにします。
数学ⅢC を学んだ皆さんは、これとよく似た図を見たことがあると思います。そう。サイクロイド(cycloid)ですね。サイクロイドはトロコイドの特別な形です。赤丸で記した動点の位置に注目してください。この動点は円の中心から好きな距離を選択できます。図では動点が円の内側に描かれていますが、外に飛び出していても構いません。この動点と円の中心の距離 rd が円の半径 rm に等しい場合に、その動点が描く軌跡のことをサイクロイドといいます。トロコイドは次のような媒介変数で表されます:
θは動円の回転角です。トロコイドの形を決定するパラメータは
動円の半径 rm, 描画点の半径 rd
の2つです。(rm, rd) を変化させながらグラフをいくつか描いてみます:

動点が円の内側にあるとき(rm > rd)に軌跡は直線から浮き上がりますね。逆に円の外側にあるとき(rm < rd)は必ず直線と交わります。
内トロコイド(Hypotrochoid)
次は定円に内接させながら円を転がすことを考えます。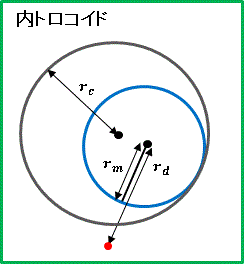
上図で動点(赤丸)の軌跡を内トロコイドといいます。
軌跡を決定する方程式は少し複雑です:
内トロコイドの形を決めるパラメータは、
定円の半径 rc, 動円の半径 rm, 描画点の半径 rd
の3つです。 rc = 2.5, rm = 1, rd = 0.8 でグラフを描いてみます:

グラフは省略しますが、rc = 2rm の関係にあれば軌跡は楕円となります。楕円は内トロコイドの特別な形ということになります。
動点を円周上にとったとき(rm = rd)の軌跡を特に内サイクロイド(hypocycloid)といいます。漢字で書くと内擺線(ないはいせん)。rc = 3, rm = rd = 1 のグラフを見てみましょう:
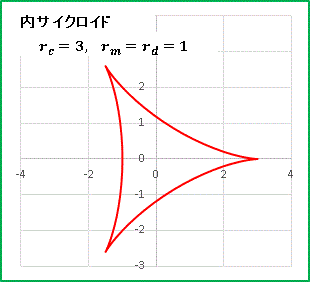
歪んだ三角形のような形が現れましたね。
rc = 4, rm = rd = 1 とすると・・・・・・

よく知られたアステロイド(asteroid)です。アステロイドは内サイクロイドの1種なのです。 rc が整数であれば、内サイクロイドの頂点の数は rc に一致します。
外トロコイド(Epitrochoid)
定円に外接しながら転がる場合は外トロコイドとよばれ、次のような方程式であらわされます:外トロコイドの形を決めるパラメータは、
定円の半径 rc, 動円の半径 rm, 描画点の半径 rd
の3つです。パラメータが多いうえに、どの記号も似通っているので紛らわしいのですが、
rc の c は center(中心点)
rm の m は move(動き)
rd の d は draw(描画)
のように記号の意味を覚えておくと多少は混乱を防げます。
外トロコイドのグラフを2つ載せておきます:

動点を円周上にとれば外サイクロイド(epicycloid)となります。
(rc, rm, rd) = (4, 1, 1) のグラフを載せておきます:

さらに rc = rm とすれば、去年の暮れに解説したカージオイド(心臓形)となります。
最後に外トロコイドの式を少し変形してみます。
トロコイドは円の転がる軌跡と定義されているので暗黙の了解として
rc > 0, rm > 0, rd > 0
という条件が要請されています。しかし数学は物理学と異なるので、このような条件を取り払ってしまうことは自由です。そこで外トロコイド方程式において rd と rc を負の値に設定してみたらどうなるのかと思い、Excel で実験してみました。するとこのように見事な形のグラフが生まれました:

もちろんパラメータの選び方によってグラフの形は様々です。
皆さんもぜひエクセルで色々な実験に挑戦してみてください!
⇒ 案内板をお試しください