極値の有無の境目を判定します
今回は一見したところとても易しそうなy = exp(x) - ax 2 [1]
という関数を扱います。 a の値をいくつか選んでグラフを描いてみます。
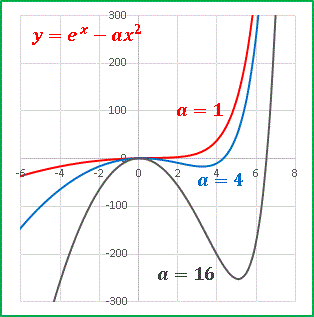
a の値を大きくするほど深い谷を形成して exp(x) の増加を遅らせます。実はこの関数は a の変遷過程である所を境に「極値をもたない関数」から「極値をもつ関数」へと変化します。その様子を調べるために、[1] を微分して導関数を得ます:
y′ = exp(x) - 2ax [2]
この導関数のグラフも描いてみます。
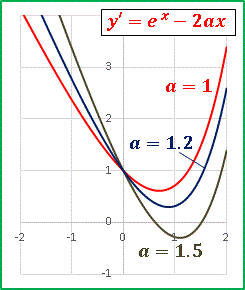
y′ のグラフが x 軸と交点を持てば [2] は極値をもちます。
a = 1.2 ではまだ極値はありませんが、a = 1.5 は極値ありです。
そこで a の値を変化させて「どこで x 軸と接するか」ということを調べます。これは VBA でプログラムを書いて計算させるわけですが、簡単にその構造を説明すると「 a の値を 0.001 刻みに変化させて、y′ の値が1つでも負の値をとった瞬間に計算を止めて、そのときの a を閾値とみなす」というものです。正確に言えば、「計算を止めた a 」と、「その直前の a 」との間に閾値があります。刻み幅を小さくすればより精度の高い値を得ることができます。実際にそのプログラムを実行すると、次のような結果を得ます。
a = 1.360 で計算終了
x = 0.96 y = 0.000496
x = 0.97 y = - 0.000456
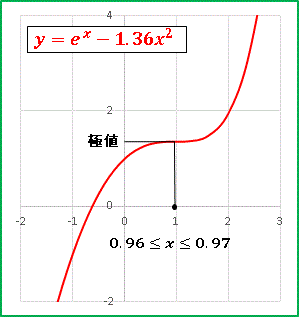
a = 1.360 が閾値です。この値を近似的にグラフが x 軸に接する a であると考えると、このとき y′= 0 の解 x = xm はひとつだけであり、 x = xm の前後で y′の符号は変化しません。したがって極値はもちません。ただ厳密に考えると a = 1.360 で僅かに x 軸と交差しているので y′ = 0 の解は2つあり、その解 α と β (α < β)は非常に近い値をとります。そしてその前後で y′ もまた微妙に変化して、x = α のところで上に凸(極大値)、x = β のところで下に凸(極小値)が現れます。ごく狭い範囲に極大値と極小値が出現しているのです。文章でずらずら書いても何が何だかわからなくなりそうなので、a = 1.370 としたグラフで極値付近を範囲を拡大してみます:
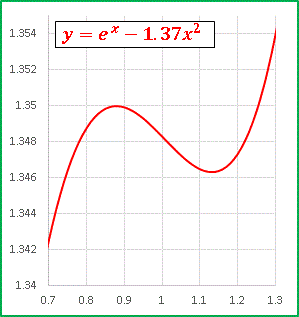
ちゃんと凹凸が現れています。
x = α = 0.88 のとき極大値 1.350
x = β = 1.14 のとき極小値 1.346
x = β = 1.14 のとき極小値 1.346
となります。極大・極小といっても普通のグラフでは目に見えない程度の小さな起伏です。
⇒ なんとなくの数学日記(新しいブログを始めました)