�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2024�N01��03��
2024�N�͑�ςȍЊQ�Ŏn�܂��Ă��܂��܂����B
2024�N���U�͓��^�C�T�b�J�[���ېe�P�����Ŗ��J���A�ۑ�͂��������̂�5-0�ŏ���������K��̗ǂ��X�^�[�g������ƕ�����Ă����Ƃ���ɁA�\�o�����̐�[�t�߂�k���Ƃ���}�O�j�`���[�h7.6�A�ő�k�x7�̑�n�k���������܂����B
�n�k�̐k���n�̏ꏊ�E�[�x���C�ݕt�߂ł������A�����Ƃ����ԂɒÔg�������r��Ȕ�Q�������炵�܂����B����ɒn�k�ɂ���Q���傫�������҂������o�Ă���Ƃ̕��܂����B
2���ɂ́A��Вn�Ɏx��������A�����邽�߂ɔ��i���悤�Ƃ����C��ۈ����̔�s�@�Ɛ��������i�`�k�̗��q�@���H�c��`�̊����H��ŐڐG�A���@�Ƃ����シ�鎖�̂��������܂����B
���q�@�̏�q�͑S�������ɒE�o�ł����悤�ł����A�C�ۂ̍q��@�̓������6�l��5�l�����S��1�����d�ǂƂ�����ςȎ��ԂɂȂ��Ă��܂��܂����B
�n�k�E�Ôg�ɔ�Ђ������X�̈��S�̊m�ہA�s���s���҂̐v���ȑ{���A���C�t���C���̑��}�̕������X���ƃ��x���őΉ����Ȃ���Ȃ�Ȃ����Ƃ��R�قǂ���܂��B�������݂Ȏ��ԂƂ̏����ł��B���q���A�x�@�A���h�ȂǍ��ƃ��x���̑g�D�������ē��ʂ̊�@�I��Ԃ̉����ɓw�߂Ă��܂��B
�n�k�̐k���n�̏ꏊ�E�[�x���C�ݕt�߂ł������A�����Ƃ����ԂɒÔg�������r��Ȕ�Q�������炵�܂����B����ɒn�k�ɂ���Q���傫�������҂������o�Ă���Ƃ̕��܂����B
2���ɂ́A��Вn�Ɏx��������A�����邽�߂ɔ��i���悤�Ƃ����C��ۈ����̔�s�@�Ɛ��������i�`�k�̗��q�@���H�c��`�̊����H��ŐڐG�A���@�Ƃ����シ�鎖�̂��������܂����B
���q�@�̏�q�͑S�������ɒE�o�ł����悤�ł����A�C�ۂ̍q��@�̓������6�l��5�l�����S��1�����d�ǂƂ�����ςȎ��ԂɂȂ��Ă��܂��܂����B
�n�k�E�Ôg�ɔ�Ђ������X�̈��S�̊m�ہA�s���s���҂̐v���ȑ{���A���C�t���C���̑��}�̕������X���ƃ��x���őΉ����Ȃ���Ȃ�Ȃ����Ƃ��R�قǂ���܂��B�������݂Ȏ��ԂƂ̏����ł��B���q���A�x�@�A���h�ȂǍ��ƃ��x���̑g�D�������ē��ʂ̊�@�I��Ԃ̉����ɓw�߂Ă��܂��B
2022�N05��29��
�u�[���_�̓`���v�u���X�E�I�u�E�U�E���C���h with �L���i�P�`�T�j
�u�[���_�̓`���v�u���X�E�I�u�E�U�E���C���h with �L���F�Ђ������蓹���܂�
YouTube�ŃQ�[���������Ă���̂��ϐ�i�ӏ܁j����Ƃ����J�e�S���[������܂��B�i�z���}�ł����H�j
�v���싅���ϐ킵����A�v���������ϐ킵����A�]�����ϐ킷��Ƃ����K��������悤�ɁA�Q�[�����ϐ�i�ӏ܁j�͂���ł��傤�B��-�X�|�[�c�����邵�ˁB
�������̂Ƃ���A�u�[���_�̓`���v�u���X�E�I�u�E�U�E���C���h�́A���N�O�ɔ������ꂽ�Q�[���\�t�g�ł��B�L�����ȊO�̑����̃Q�[���nYouTuber���u���X�E�I�u�E�U�E���C���h�̓����YouTube�ɃA�b�v���Ă��܂��B
�Q�[���\�t�g�ɓ��݂���o�O���ő�����p���āA�X�^�[�g����Q�[�������܂ł𐢊E�ő���ڎw���ċ����������������A����Q�[����l���̊����͈́i�\�́j�̔����݂��Ă���݂̂ŃQ�[�������܂œ˂��i�ޓ��������܂��B
�L�����̓���̓����́A�ߋ������ǂ��u�[���_�̓`���v�̃Q�[�����o�����Ă��Ȃ��A�Ƃ������Ƃł��B�u���X�E�I�u�E�U�E���C���h�����̌��ł���A������̓��悪�����ł���Ƃ������Ƃł��B
���߂āu�[���_�̓`���v�u���X�E�I�u�E�U�E���C���h��m��ЂƂɂƂ��Ă��y���߂铮��ɂȂ��Ă��܂��B

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#1

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#2

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#3

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#4

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#5
�g�[�^��6����02��17�b�A
�܂��܂������͑����Ă��܂��B
YouTube�ŃQ�[���������Ă���̂��ϐ�i�ӏ܁j����Ƃ����J�e�S���[������܂��B�i�z���}�ł����H�j
�v���싅���ϐ킵����A�v���������ϐ킵����A�]�����ϐ킷��Ƃ����K��������悤�ɁA�Q�[�����ϐ�i�ӏ܁j�͂���ł��傤�B��-�X�|�[�c�����邵�ˁB
�������̂Ƃ���A�u�[���_�̓`���v�u���X�E�I�u�E�U�E���C���h�́A���N�O�ɔ������ꂽ�Q�[���\�t�g�ł��B�L�����ȊO�̑����̃Q�[���nYouTuber���u���X�E�I�u�E�U�E���C���h�̓����YouTube�ɃA�b�v���Ă��܂��B
�Q�[���\�t�g�ɓ��݂���o�O���ő�����p���āA�X�^�[�g����Q�[�������܂ł𐢊E�ő���ڎw���ċ����������������A����Q�[����l���̊����͈́i�\�́j�̔����݂��Ă���݂̂ŃQ�[�������܂œ˂��i�ޓ��������܂��B
�L�����̓���̓����́A�ߋ������ǂ��u�[���_�̓`���v�̃Q�[�����o�����Ă��Ȃ��A�Ƃ������Ƃł��B�u���X�E�I�u�E�U�E���C���h�����̌��ł���A������̓��悪�����ł���Ƃ������Ƃł��B
���߂āu�[���_�̓`���v�u���X�E�I�u�E�U�E���C���h��m��ЂƂɂƂ��Ă��y���߂铮��ɂȂ��Ă��܂��B

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#1

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#2

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#3

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#4

���E����^�����j��ō��̐_�Q�[�w �[���_�̓`�� �u���X �I�u �U ���C���h �x#5
�g�[�^��6����02��17�b�A
�܂��܂������͑����Ă��܂��B
posted by �p�v���J2020 at 09:02| �i�J�e�S���Ȃ��j
2022�N02��10��
�O�p�`�̖ʐς����߂�
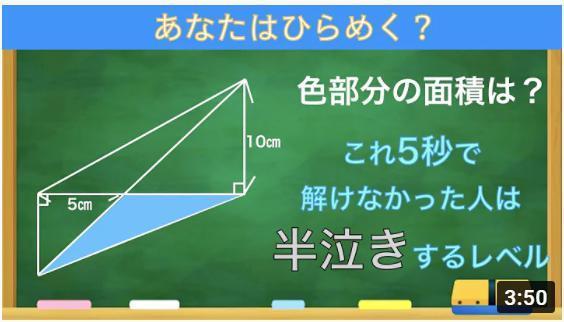
Q�F�F�œh��Ԃ��ꂽ�O�p�`�̖ʐς����߂�B
�`�F
�}�̂悤�Ɋe��_��A�`E�Ƃ���

AE��BC�͕��s�AAE��EB��BC
���߂�ʐςr��
�r����ABC�̖ʐςr1�|��DBC�̖ʐςr2
������
�r1��10*(5�{x�j*(1/2)
�r2��10*x*(1/2)
���ӂ͓���BC�A��ABC�̍���BE�A��DBC�̍���BD
�����
�r���r1�|�r2
�@��10*(5�{x�j*(1/2)�|10*x*(1/2)
�@��10*5*(1/2)�{10*x*(1/2)�|10*x*(1/2)
�@��10*5*(1/2)
���r��25c�u
posted by �p�v���J2020 at 00:00| �i�J�e�S���Ȃ��j
2022�N02��09��
�����`�̖ʐς����߂�
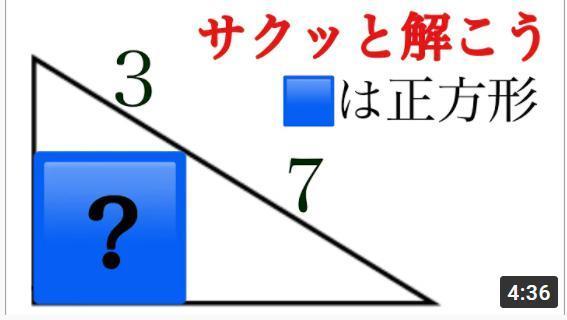
Q�F�F�œh��Ԃ��ꂽ�����`�̖ʐς����߂�B
�`�F
�����`�̈�ӂ̒�����x�Ƃ���B
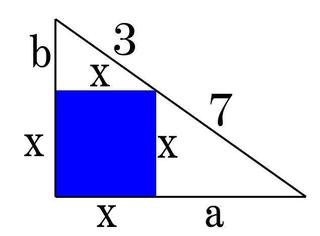
�Εӂ�3�A7�A10�i��3�{7�j�̒��p�O�p�`�͑S�đ����`�B
�����3�Fx��7�F��
��7*x��3*a
����������
a��(7/3)*x
�܂��A7�Fx��3�Fb
��3*x��7*b
����������
b��(3/7)*x
�ȏ���
x�{b��x�{(3/7)*x��(10/7)*x
x�{a��x�{(7/3)*x��(10/3)*x
�^����ꂽ���p�O�p�`�̊e�ӂ̔��
10�F(10/7)*x�F(10/3)*x
��1�F(x/7)�F(x/3)
��21�F3*x�F7*x
����ĎO�����̒藝��p����
9*x^2�{49*x^2��21^2
(9�{49)*x^2��441
x^2��441/58
�����`�̈�ӂ̒�����x�������̂�
�����`�̖ʐς́@441/58
�@�@
posted by �p�v���J2020 at 01:07| �i�J�e�S���Ȃ��j
2022�N01��24��
�`�����{���C�a����*���̂Ƃ���^4�{��^4�́H

�`�����{���@�E�E�E�@
�a����*���@�@�E�E�E�A
��^4�{��^4�@���`�C�a��p���ĕ\���B
�@�̗��ӂ�2�悷��B
�`^2����^2�{2*��*���{��^2�@�E�E�E�B
�A����B�́A
�`^2����^2�{2*�a�{��^2
�i�`^2�|2*�a�j����^2�{��^2�@�E�E�E�C
�C�̗��ӂ�2�悷��B
�i�`^2�|2*�a�j^2����^4�{2*��^2*��^2�{��^4�@�E�E�D
�D�͇A����A
�i�`^2�|2*�a�j^2����^4�{2*�a^2�{��^4�@�E�E�E�E
�E��2*�a^2�����ӂɈڍs����B
�i�`^2�|2*�a�j^2�|2*�a^2����^4�{��^4�@�E�E�E�F
����^4�{��^4���`^4�|4*�`^2*�a�{2*�a^2
posted by �p�v���J2020 at 21:14| �i�J�e�S���Ȃ��j
2022�N01��23��
��̓h���}����
2022�N�̑�̓h���}�́u���q�a��13�l�v�ł��B�����ɋA�Ȃ����ۂɕꂪ�ǂ����Ă��������Ƃ������Ƃł��t�������Ō��܂����i�ŋߑ�̓h���}�ɋ����͂Ȃ��Ȃ��Ă����̂ł����j�B���O�������납�����ł��ˁB
�����������Ȃ�퍑����ł����A���q����̏��������͂������납���A�ł��B
���킹��YouTube�ő����̂ЂƂ����������A�b�v���Ă��āA�{��+YouTube�ł������낳�{���ł��B
�o��l���͑����̂ł����A�Ƃ肠�����k���Ƃ̖��҂̊F�l�ɒ��ڂ��Ęb�����āA��ق�YouTube�̉���Łu�Ȃ�قǁA�����������̂��`�v�Ǝv���킯�ł��B

�����������Ȃ�퍑����ł����A���q����̏��������͂������납���A�ł��B
���킹��YouTube�ő����̂ЂƂ����������A�b�v���Ă��āA�{��+YouTube�ł������낳�{���ł��B
�o��l���͑����̂ł����A�Ƃ肠�����k���Ƃ̖��҂̊F�l�ɒ��ڂ��Ęb�����āA��ق�YouTube�̉���Łu�Ȃ�قǁA�����������̂��`�v�Ǝv���킯�ł��B

posted by �p�v���J2020 at 21:08| �i�J�e�S���Ȃ��j
2021�N12��10��
������������
posted by �p�v���J2020 at 00:00| �i�J�e�S���Ȃ��j
2021�N12��09��
�A��������

Q
�A��������
x-y=25
sqrt(x)+sqrt(y)=25
������
�`
sqrt(x)=X
sqrt(y)=Y
�ƒu���ƁA
�^����
X^2-Y^2=25�@�E�E�E�@
X+Y=25�@�E�E�E�A
�@��
(X+Y)(X-Y)=25
�����ɇA�����������
X-Y=1�@�E�E�E�B
�A+�B
2*X=26
X=13�@�E�E�E�C
X=sqrt(x)������
sqrt(x)=13
��x=169
�܂��C���B�������
13-Y=1
��Y=12
����������
y=144
Ans.�@(x,y)=(169,144)
posted by �p�v���J2020 at 00:00| �i�J�e�S���Ȃ��j
2021�N12��08��
�⏕�������邩��

�p
�^����ꂽ�O�p�`�̒�ӂ̒����w�̒l�����߂�B
�`
�^����ꂽ�O�p�`����ABC�Ƃ��āA�e���_�����}�̂悤�Ɋ���U��B

��A=2*��B�ł���B
���_A�����A�̂Q�������������ABC�Ƃ̌�_��D�Ƃ���B
BD=a
CD=b
�Ƃ����B
5:a=4:b
4*a=5*b
��a=(5/4)*b�@�E�E�E�@
��ABC�䇙DAC
���B=��DAC�A��C�͋���
b:4=4:(a+b)
b*(a+b)=16
�@�����������
b*((5/4)*b+b)=16
(9/4)*b^2=16
b^2=16*4/9
��b=8/3�@�ib>0�j�@�E�E�E�A
�A���ɇ@�����������
a=(5/4)*(8/3)=10/3�@�E�E�E�B
X=a+b������
X=(8/3)+(10/3)=18/3=6
posted by �p�v���J2020 at 00:00| �i�J�e�S���Ȃ��j
2021�N12��07��
x^2+y^2=?
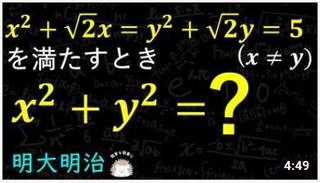
Q
x^2+sqrt(2)*x=y^2+sqrt(2)*y=5
�����Ƃ��@�ix��y�j
x^2+y^2=?
�`
x^2+sqrt(2)*x=5�@�������̌`�ɂ���B
x^2+2*(sqrt(2)/2)*x+(sqrt(2)/2)^2-(sqrt(2)/2)^2=5
(x+(sqrt(2)/2))^2=5+(1/2)=11/2�@�E�E�E�@
y^2+sqrt(2)*y=5�@�ɂ��Ă����������̌`�ɂ���B
(y+(sqrt(2)/2))^2=11/2�@�E�E�E�A
�����Ň@+�A�ɂ����
(x+(sqrt(2)/2))^2+(y+(sqrt(2)/2))^2=11
����́A���W(-sqrt(2)/2,-sqrt(2)/2)�𒆐S�Ƃ��锼�asqrt(11)�̉~�̕������ł���B
���̉~�̒��S��(0,0)�Ɉړ��������̂�
x^2+y^2=?�@
�ł��邩��A�^����11�ł���B
posted by �p�v���J2020 at 00:00| �i�J�e�S���Ȃ��j