パプリカ2020の部屋

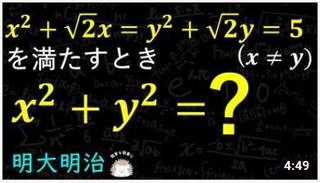
Q
x^2+sqrt(2)*x=y^2+sqrt(2)*y=5
を満たすとき　（x≠y）
x^2+y^2=?

Ａ
x^2+sqrt(2)*x=5　を平方完成の形にする。
x^2+2*(sqrt(2)/2)*x+(sqrt(2)/2)^2-(sqrt(2)/2)^2=5
(x+(sqrt(2)/2))^2=5+(1/2)=11/2　・・・�@

y^2+sqrt(2)*y=5　についても平方完成の形にする。
(y+(sqrt(2)/2))^2=11/2　・・・�A

ここで�@+�Aにすると
(x+(sqrt(2)/2))^2+(y+(sqrt(2)/2))^2=11

これは、座標(-sqrt(2)/2,-sqrt(2)/2)を中心とする半径sqrt(11)の円の方程式である。

この円の中心を(0,0)に移動したものが
x^2+y^2=?　
であるから、与式は11である。