アフィリエイト広告を利用しています
<< x^2-5*x+1=0のとき、x^2+(1/x^2)の値を求めよ。 | TOP | x^2+y^2=? >>

2021年12月06日

円に内接する扇型の面積を求める。

円に哀切する扇型.jpg

Ｑ．
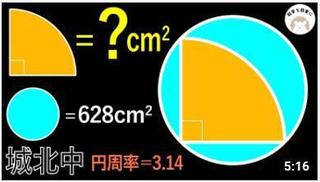
円に内接する扇型の面積を求めよ。
円の面積は628㎠、円周率は3.14である。
ただし扇型の要の角度は90°である。

Ａ．
円に内接する３点のうち、扇の要でない2点を結ぶ直線は円の直径である。
円の半径をrとすると
r*r*3.14＝628㎠
となり、r*r＝200㎠

円の直径を対角線とする正方形の面積は
(2*r)*(2*r)＝4*r*r＝800㎠
扇型の一辺の長さをaとしたとき
aを一辺とする正方形の面積は
a*a＝(800/2)㎠＝400㎠

求める扇型の面積は
a*a*3.14*(90°/360°)＝314㎠
Share on Tumblr
【このカテゴリーの最新記事】
posted by パプリカ2020 at 03:52| Comment(0) | TrackBack(0) | （カテゴリなし）
この記事へのコメント
コメントを書く

お名前:

メールアドレス:


ホームページアドレス:

コメント:

この記事へのトラックバックURL
https://fanblogs.jp/tb/11135162

※言及リンクのないトラックバックは受信されません。

この記事へのトラックバック
ファン
 このブログの読者になる
 更新情報をチェックする
 ブックマークする
 友達に教える
検索
<< 2025年03月 >>
日 月 火 水 木 金 土
            1
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
30 31          
最新記事
(03/29)2030年に氷河期到来って騒いでいるけど？
(03/28)すでに世界はＡＩに牛耳られてる？
(01/03)2024年は大変な災害で始まってしまいました。
(05/29)「ゼルダの伝説」ブレス・オブ・ザ・ワイルド with キヨ（１～５）
(02/10)三角形の面積を求める
写真ギャラリー
最新コメント
タグクラウド
カテゴリーアーカイブ
プロフィール
パプリカ2020さんの画像
パプリカ2020
プロフィール
日別アーカイブ
2025年03月29日(1)
2025年03月28日(1)
RDF Site Summary