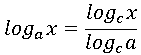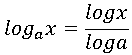Excel VBA　数学実験室

　センター試験を受験された皆さん、お疲れ様でした！　手ごたえはいかがでしたか？　「数学�U・数学B」第１問は指数・対数の問題でしたね！　「こばとの数学基礎講座　冬休み編」の最終回では、今回のセンター試験「数学�U・数学B」から対数に関する問題をちょこっと抜き出して解説してみたいと思います。

こばとの数学基礎講座19　2016 年センター試験から問題を抜粋します

　それではさっそく、


を計算する問題から。冬休み編の出だしでも言いましたけど、この手の計算はぱっと見た瞬間にわかるぐらいに訓練しておくことが必要です（時間の節約になります）。


ですから、「 27 の 3 乗根をとって 2 乗して −1 乗して 1/9 になるよね」という過程を頭の中でスムーズに進めていかなくてはなりません。答えは


となります。この計算感覚は対数関数のグラフの対称性を答える次の問題でも役立ちます。

　　　　(a) y = log₂x と y = log_1/2x
　　　　(b) y = log₂x と y = log₂1/x

の関係性を問われましたね。x に具体的な真数を入れて考えてみます：

　　　　(a) y = log₂4 と y = log_1/24
　　　　(b) y = log₂4 と y = log₂1/4

基本的にどちらも同じ思考過程を辿ります。(a) の場合は

　　　　2 を 2 乗して 4,　1/2 を 2 乗して −1 乗して 4

となりますね。(b) もまた

　　　　2 を 2 乗して 4,　2 を 2 乗して −1 乗して 1/4

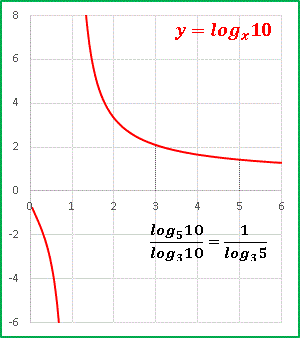
ですから y = log₂x に対して底または真数が逆数となる関数はその値が逆符号、すなわち x 軸に対して対称であることがわかります。細かく説明しましたが、対数の感覚を掴んでいればこの関係性は式の形を見た瞬間にわかります。もちろんグラフの形を知っているにこしたことはないので、エクセルグラフも載せておきます。結局のところ y = log_1/2x と y= log₂1/x は同じ関数ですよ。

　

上の３問は合わせて 15 秒で解答できるはずです！

対数の２次式


の最小値を求める設問も全くひねりがなかったので、基本に忠実に解いていけば正解に辿り着けます。マークシートなので、t = log₂x と置くことが明示されており、受験生の皆さんは置換方法を考える必要はなかったのですが、もし２次試験の記述式でこのような問題が現れたとき、２次の項に含まれている対数の底に注目して変数を置き換えるようにしてくださいね。この講座でも紹介した公式を使って


と置き換えて代入すると


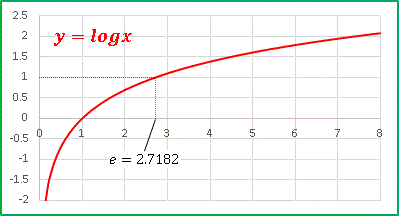
となります。x が x > 0 の範囲を動くときの t = log₂x のとりうる範囲も問われていましたが、対数関数は −∞ から ∞ までの値をとる関数です（上の y = log₂x のグラフを参考にしてください）。要するに全実数をとります。たとえば底 > 1 でグラフを描いたとき、x を増加させていくとあまりにも値の増加が緩慢なので、「もしかしてどこかに収束する？」と勘違いする人もいるかもしれませんが（実際、グラフの形を見るとなんとなくそう見えちゃったりしますが）、どれほどゆっくりしたペースであろうと x → ∞ では y = log_ax (a > 1) は確実に ∞ に発散していきます。

さて、(*) を変形して


となるので頂点の座標は (3, − 2)と求められます。
t = 3 すなわち x = 8 のとき 最小値 −2 をとります。

答えはこれでいいのですが、本編を書いている "エクセルおたく" のブログ主さんだったら


が具体的にどういうグラフなのか気になってしまうはずです。今回はこばともブログ主さんを真似して、こういう予測しにくいグラフを描いちゃったりしますよ。

　

　こういう形のグラフになります♪　原点付近で ∞ から急速に落ち込んで (8, −2) で最小値をとり、今度はそこからゆっくりと立ち上がってゆく関数ですね。といってもこれは本編で扱うほど難しいグラフではありません。数学�Vを学んだ人は微分して増減表を作って描けますので、ぜひ挑戦してみてくださいな。

　今回でひとまず「こばとの数学基礎講座」は一休みします。次は４月頃の再開を予定しています。おそらく三角関数を扱うことになると思います。４月にはこばとのお友達の小春ちゃんや沙希ちゃんも高校３年生になります。１度ぐらいはこの２人をこちらのブログに招待してみたいなと思っています。何か番外編的なテーマを１つ選んで、３人の対話形式で講座を進めていけたら面白いかもしれません。それでは春休みにまたお会いしましょう！
　 　

　年明けは思いもかけず美味しい物をいただく機会に恵まれましたよ。小春ちゃんのお家ではアンパンを、小夜子さんのとこではロイズのチョコレートをご馳走になりました。ちょー美味しかったですねー。でもこのまえ職場（あとりえこばと）でお昼ごはん（カレーパン）を食べていたら、涼音さんとマリちゃんに「最近ぽっちゃりしてる」なんて言われてしまいました！　失礼しちゃいますね！　こばとはちっとも太ってません！　それを証明するために、今晩、体重を量ってみようと思います。でも今日は忙しいから明日にするかもしれません …… もしかすると明後日かも …… 。そのうち量りますよ。本当ですよ？　別に体重の話なんてどうだっていいんです。数学しましょう。

こばとの数学基礎講座 18　常用対数を使って大きな数の桁数を調べます

　底を 10 とする対数のことを 常用対数（common logarithm） とよびます：


　常用対数は指数表示された巨大数の桁を求める問題でよく用いられます。私たちは 10 進数 に馴染んでいるので常用対数は感覚的にわかりやすいと思います。たとえば x = 10, 100, 1000 に対して

　　　　y = log₁₀10 = 1
　　　　y = log₁₀100 = 2
　　　　y = log₁₀1000 = 3

ですね。 [0, 1000] の範囲でグラフを書いてみましょう：

　

　y = log₁₀x はとても緩慢な関数です。
　さらに大きな x に対してもなかなか値を伸ばしません。


　x が１億（10 ⁸）でも y はたったの 8 です！　上のグラフでは縦軸のスケールを大きめにとってありますが、もし縦横同じスケールの目盛で描いたとしたら、x 軸にべったりと張り付いた直線のようなグラフになってしまいます。

　常用対数を用いると 10 以外の数を底とする指数で表された数の桁を求めることができます（つまりおおよそどのくらいの数なのか概算できるということです）。たとえば


という巨大な数がいきなり目の前に現れたとき、それが十進法で具体的にどのように表されるかということは分かりませんが、桁数だけは求めることができます。


とおいて、10 を底とする対数をとると、


となります。つまり


となり、その桁数が 176 であることがわかります。

桁数は指数 +1 となることに注意してくださいね。たとえば


となります。

底の変換公式を使って、自然対数 ⇒ 常用対数の変換式も載せておきます：


2 〜 9 までの常用対数は以下のようになります：


　別に覚える必要はありませんが、ざっと眺めて常用対数値の感覚を掴んでおいてください。
　 　

≫ [Amazon書籍] とんでもなく役に立つ数学

こばとの数学基礎講座 17　底の変換公式の意味をグラフを使って考えます

　前回学んだように素数の自然対数のリストが用意されたなら、それを元にしてあらゆる対数の計算が可能となります。特に要となる計算技術が 底の変換公式 です。次のように底 a, 真数 x の対数を底 c の対数で表すことを考えます：


　導出は簡単です。y = log_a x を


の形に直して c を底とする対数をとります：



　前々回に学んだ

という公式を用いて右辺を変形します：


y = log_ax ですから


となって、


という公式が得られます。c が自然対数 e の場合は、前回取り決めたように底の表示を省略できますから、


となりますね。これでようやく前回までの宿題として残されていた


を計算することができますね。まず log₂ 5 の底を e に変換します：


　ここで前回に計算した素数の自然対数値


を用いて計算すると


となります。したがって


という値が得られますよ！　ちなみにエクセルでより正確な値を求めてみると、


ですから、小数点以下３桁までの精度で計算できたことになります。この計算精度は前回に載せた自然対数の級数展開で何項まで計算するかで決まります。ちなみにエクセルのような表計算ソフトも内部では級数を使って関数を計算しています。しかし昔の人は電卓すらなかったわけですから、コツコツと手計算で膨大な計算をして対数表を作っていたのです。本当に頭が下がる思いですね。

　さてここからは底の変換公式のもつ意味を視覚的に解説していきます。

　２通りの方法で説明を試みます。
　まず最初に底が 2 と 10 である２つの対数関数


のグラフを描いてみます：

　

1 < x の範囲では log₂x が log₁₀x の上にきます。直感的にわかる人もいると思いますが復習も兼ねて一応確認しておきます。たとえば x = 10 という値で考えたときに、


となりますね。明らかに


となります。そこで log₂ x の底を 10 に変換することを考えてみます：


となりますね。ここで右辺の


という数は log₂ x と log₁₀ x の比率を表しているのです。しかもその比は真数 x がどういう値をとっても一定です。言い換えるなら、「 log₂x をどうしても log₁₀ x を含む形で表したいのであれば、係数 3.32193 という値を掛けて調整しなければなりませんよ」ということなのです：


それでは２つめの方法で説明してみます。こちらはたった１つのグラフでより本質的な見方ができます。用いる関数は普通の対数関数ではなく、真数を固定して底を変数とする


という関数です！　普段はあまり見ることのない形ですね。指数形式に直すと


という関係ですが、やはりこんな表式はほとんど見る機会はないと思います。とりあえずグラフを描いてみましょう。

　

今は 1 < x の範囲で説明します。x = 1 付近から急激に値を減らしていきますが、x が大きくなるにしたがってその減少率は緩やかになっていきます。このグラフは「真数 10 について、底が増加したときその対数値はどうなっていくのか」ということを明確に表しています。そこでたとえばこのグラフ上の２点


を抜き出して比較したとき、その減少率は底の変換公式における係数になっているはずですね。つまり log₅10 を log₃10 を含む形で表したいのなら、 log₃10 は大きすぎるので


という変換で log₃ 10 に係数を乗じて値を減少させなければならないということです。

本日はここまでです！　それではまた次回お会いしましょう！
（暇があるなら、こばとの雑談を読んで帰ってくださいな）

こばとの雑談

　前回、向こうの世界ではネイピア数 e のことを "コンダ" と呼ぶとお話しましたね。
　今回は e⁰ や e¹ の呼び方です。
　0 はエン・エラカダ語（古エラカダ語）で "エン" と発音します。
　"エン" は「無」や「真空」を第１義としますが、
　「不動、永遠、太古」という意味もあります。
　e⁰ は "エン・コンダ" と言います。
　底が e の場合に限って「〜乗」を意味する "ク" を省略できるのです。
　1 は "ヴィ" なので e¹ は "ヴィ・コンダ" 、
　2 は "パズ" だから e² は "パズ・コンダ" 。
　未知数 x に相当するエラカダ語は "チェカ" です。
　なので e^x は "チェカ・コンダ" となります。
　まあでも、こちらの世界とあちらの世界、書き方・読み方が違っても数学の本質的な部分は全く同じですね。数学は自然界を表記する手段ですから、世界が異なっていても物理法則が同じならば必然的に数学もまた同一のものとなってしまうのは当たり前なことなのかもしれませんけどね。
　物理法則と言えば、その昔、姉は古風な手段を使って一生懸命に万有引力定数や電子のもつ電荷などを調べたことがあるそうです。「観測できる範囲内で数値は全く同じ。びっくりした」とは姉の言葉。「もしかして同じ宇宙の遠い惑星に来てしまったのかと錯覚しそうだった」とも言っていました。こばとは物理学に関してはそれほど詳しくないのでなんともいえないのですが、不思議なこともあるものですね。
（注：エン・エラカダ語のカタカナ語表記はかなり適当です。"エン" は "イェン"、"パズ" は "プァズ" と表記したほうがまだ原音に近いかもしれませんが、そもそもカタカナ語で表すこと自体にかなり無理があります。そして何より私自身のエラカダ語の発音がとーっても怪しいのです。母国語のスカヴア語は姉にみっちり仕込まれましたけど、エラカダ語はこばとたちにとっても完全に外国語です。数学・科学用語は借用されていましたけど、それはつまりスカヴア語風に発音されてしまうわけです。いや、そもそもエン・エラカダ語は古い時代のエラカダ語だから、現代エラカダ語とは発音がだいぶ変わっているだろうし・・・・・・こんなややこしいことをつらつら書いても誰も読んでいないかもしれませんね。もうこのへんでやめとこうっと）
　 　

≫ [Amazon書籍] 食える数学（角川ソフィア文庫）

こばとの数学基礎講座 16　ネイピア数と自然対数

　円周率と並んで数学で最も大切な定数がネイピア数（Napier's number）"e" です。発見者であるスコットランドの数学者 ネイピア（John Napier） にちなんだ呼び名です。ネイピア数は無理数で


という値をもっています。 e はとても不思議な数です。 e を底とする指数関数


という曲線を考えたとき、曲線上の任意の点における接線の傾きがこれまた


という形で表されます：

　

当ブログでは y = e ^x のことを


と表記する場合もあります。exp は exponential（指数関数）の略です。

y = e^x の逆関数である


のことを自然対数（natural logarithm）と呼びます。多くの数学書と同様に、当ブログでも自然対数の場合に限って底の表記を省略して簡単に


と書くことにします。ただ、本によっては自然対数を


と表記して、底を 10 とする常用対数のことを y = logx としている場合もあるので注意してくださいね（たいていは本の最初の方に記述ルールに関して触れてあるはずです）。

　

　さて今回からいよいよ「正確な対数値」を求める作業に踏み込んでいきます。その土台となるのが「素数の自然対数」なのです。sinx や cosx, 或いは logx のような連続関数は x の級数の形で表すことが可能であることが知られています。その表式を得るための手順は高校数学の範囲を超えるため省略しますが、表式自体は簡単です。まずは log2 を得るためにたった１回だけ

　　

という式を使います。 x = 1/3 のきに左辺が log2 となることを確認してください。右辺は単調で面倒な計算をひたすら行って（皆さんは計算しなくていいですよ）、


という高い精度の値が得られます。そして log3 以降は次式を繰返し使うことになります：

　

　上式から素数の自然対数を次々に得ていきます：


　こうして得られた素数の自然対数を用いれば、前回学んだ公式を用いて合成数の自然対数を求めることができます。たとえば


というように計算できるわけです。これで前回の宿題として残された


が計算できそうな気もしますが、残念ながらまだです。よく見てください。求めたいのは


の値です。底が違っています。そこで次回では「底の変換公式」を学びます。特に次回はおそらくどの本にも載っていないようなびっくりするような手法で公式を解説しますよ！　お楽しみに！

こばとの雑談

　余談ですが、こばとの故郷（こばとの卵が創られた世界）ではタビ・モラシャンというエラカダの哲学者によって自然対数の底が発見されましたが、その定数に彼の名前が付けられることはありませんでした。その数は "コンダ" と呼ばれていたようです（念のため言っておくと、こばとの卵が "孵化" したのはこちらの世界なので、向こうの世界のことは全て姉から教わった知識です。だから細部で間違いもあるかもしれません）。"コンダ" とは「土台、基礎、拠点（転じて砦・要塞などの頑強な建造物）」を意味する言葉です。それだけ数学にとって普遍的で大切な定数という意味なのですが・・・・・・うーん・・・・・・ちょっと味気ない気もしますね。なんだかごつい響きだし。こばとはこちらの世界の "ネイピア数" という呼び名のほうが気に入っています♪
　 　

≫ [Amazon書籍] 教科書では教えてくれない!　ほんとうに使える数学

こばとの数学基礎講座 15　対数計算で用いる公式

　対数の概念を用いる大きな動機の１つとして、たとえば「 100 という数字を何とか 2 ^k のような形で表したい」という要求があります：


　2⁶ = 64, 2⁷ = 128 ですから、その数 k は 6 と 7 の間にあって明らかに整数ではありませんが、「それでもいいから、ともかく表したい」と我儘を言うのです。何とか


を求めることができれば、


と表記できますね。要はこの「肩に乗っている無理やりに作った指数」が「対数」なのです。しかし今の段階ではまだ計算することはできません。いくつかの計算規則を導いておく必要があります。今、R, S という２つの数を用意して、底を a とする指数の形に表せたとします：


そこで積 RS を作ってみると、指数法則により


となりますね。右辺の指数部分が RS の対数なのですから、


という公式が得られます。新しい公式というよりは指数法則の書き直しですね。 R/S をつくれば同じようにして


を得ることができます。また R ^t をつくると、


ですから、


という公式も得られます。以上３つの公式をまとめておきます：


それでは改めて log₂100 の計算に挑戦してみましょう。


と分解できますから先程の公式を用いると、


と計算できます。あとは log₂5 を求めることができれば、求める値を得ることができますよ！　・・・・・・でもどうやって？　実はこれがかなりの難問なのです。対数計算において真数を素因数分解して何とか答えに近づいても、結局最後には「素数の対数」というものが残ってしまいます。「素数の対数」を計算することは避けられません。それには大学レベルの微積分の知識が必要となりますが、次回以降、このあたりの流れを難しくなりすぎないように丁寧に解説していく予定です。