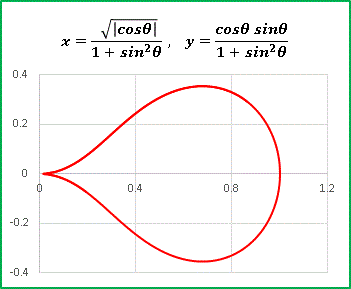
円と四角形の狭間にある図形
皆さんもよくご存知のように、
x = cosθ, y = sinθ
は媒介変数θで表された円の方程式ですね。では
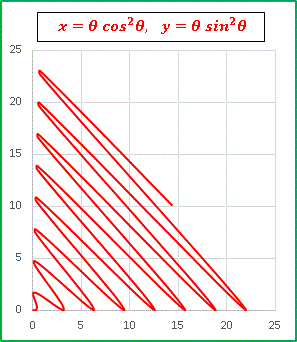
x = cos 2 θ, y = sin 2 θ
はどんな図形を表す方程式でしょうか?
「こんな方程式見たことない!」
と驚く人もいるかもしれませんが、落ち着いてください。
x + y = cos 2 θ + sin 2 θ = 1
ですから、ただの直線です(正確にいうと x, y ≧0 定義される半直線)。
わざわざ媒介変数表示する人なんていません。
しかしたとえば、指数が 1 と 2 の中間点にあるような場合:
x = cos 1.5 θ, y = sin 1.5 θ
これはどういう図形を表しますか?
数学に強い人なら即座に「定義できない!」と答えるでしょう。
そうですね。三角関数は負の値をとる場合がありますから、
x = (-1) 1.5
というような計算を実数の範囲で定義することはできません。
もちろん複素関数を用いれば定義できますが、このブログではなるべく高校生にも理解できるように話を展開したいので、今の段階ではまだ複素関数を扱いません(こばとちゃんの基礎講座の進み具合を見ながら考えます)。
さて、全ての実数 p に対して
x = cos p θ, y = sin p θ
というような方程式を定義したい場合はどうしたらいいのでしょう?
もちろん単純に sinθ や cosθ の絶対値をとるというわけにはいきません。
そんなことをすると (x, y) は第1象限に限定されてしまい、円を描くことさえできません。あくまで円を含むような形で、きちんと閉曲線になるように定義し直したいのです。そこで各象限ごとの三角関数 sinθ, cosθ の符号を改めて下図で確認してみましょう:
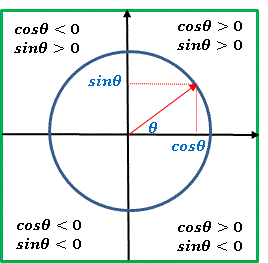
このような符号の移り変わりを保ったままで、新しい方程式の定義を考えたいのです。そこで三角関数をそれ自身の大きさで割ってみることにします:
a(θ) = cosθ/|cosθ|, b(θ) = sinθ/|sinθ|
a(θ) も b(θ) も確かに θ の関数ではありますが、1 か -1 の値しかとりません。象限が変わる毎に 1 と -1 の間を遷移するだけです。象限毎の符号は元の三角関数と同じです。そこでこの関数を用いて、
x = a(θ) |cosθ| p = cosθ |cosθ| p - 1
y = b(θ) |sinθ| p = sinθ |sinθ| p - 1
という関数を作れば本質的な意味で
x = cos p θ, y = sin p θ
を定義したと考えることができます。
ここで p ≧ 1 と決めておくと、この方程式は途切れなく続く閉曲線になります。
それでは p = 1.0 ~ 2.0 まで変化させながら、
新しい方程式の描く図形を見ていきましょう:

真円から少しずつ変化して正方形に変化していく様子が見てとれますね。
p = 1.4 や p = 1.6 は正方形と円の中間にあるような形容しがたい図形です。
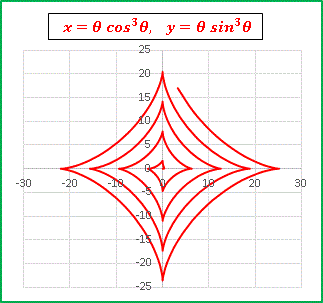
さらにパラメータを動かして図形の変化を追います:

今度は正方形の各辺が少しずつたわんで最終的にはアステロイド(p = 3.0)に変化しました! つまり、この方程式は円、正方形、アステロイドを全て含むことになります。
さらに p を増やしていくとアステロイドはどんどん潰れていきます。
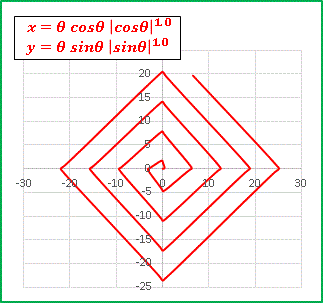
たとえば p = 10 の図形を描くと・・・・・・
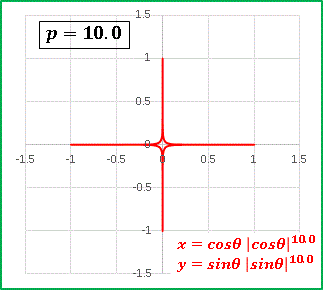
閉曲線内の面積はもはや見えないほど小さくなっていますね。
p → ∞ の極限で2本の線分が交差するような図形になりますが、それでも「閉曲線である」という事実には変わらないのです。
⇒ なんとなくの数学日記