これからのためのブログ

５月３日は憲法記念日で祝日です。

今日からＧＷという方もいらっしゃるでしょう。連休で遠出する方もいると思いますが、はりきって問題を解きましょう。





問
外接円の半径が３である△ABCを考える。
点Ａから直線ＢＣに引いた垂線と直線ＢＣとの交点をＤとする。

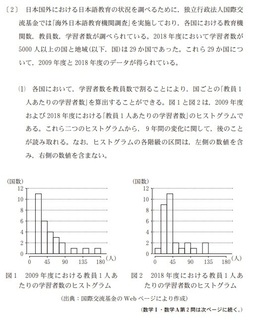
(1)　ＡＢ＝５、ＡＣ＝４とする。このときのsin∠ABC、ADを求めよ





では、解説していきます。

この設問では、正弦定理を使います。
正弦定理は、三角形の内角とその対辺の長さの比が外接円の半径の２倍と同じというものです。

まず、分かりやすくsin∠ABCをθ、外接円の半径をｒとします。



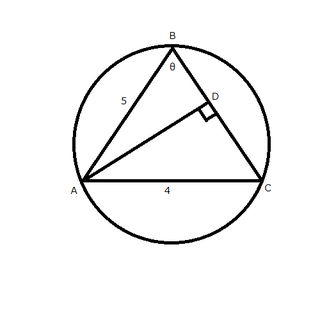
ＡＣ／sin∠ABC＝２ｒ

４／θ＝６

６θ＝４

θ＝２／３　となります。





次に、ＡＤを求めます。

これは三角比の基本、sin∠ABC＝ＡＤ／ＡＢ　を使います。

２／３＝ＡＤ／５

ＡＤ＝１０／３　となります。





(2)　ＡＢ、ＡＣに２ＡＢ＋ＡＣ＝１４という関係があるとき、ＡＢの取り得る範囲とＡＤを求めよ

では、解いていきましょう。





(2)では、点Ｂと点Ｃの位置が固定されていないという問題です。

まず、ＡＢ＝ｘ、ＡＣ＝ｙとしたときに　２ｘ＋ｙ＝１４　となります。

そしてｘ、ｙともに最大でも円の直径までしか長さを取り得ないのは分かるかと思いますので、

０＜ｘ≦６　、　０＜ｙ≦６　という条件が導けます。

ここで先ほどの「２ｘ＋ｙ＝１４」から「ｙ＝１４−２ｘ」となり、これを「０＜ｙ≦６」に代入します

０＜１４−２ｘ≦６

ー１４＜−２ｘ≦−８

７＜ｘ≦４　という条件が導けます。「０＜ｘ≦６」と「４≦ｘ＜７」の２つを合わせて、

４≦ｘ≦６　がＡＢの取りうる範囲になります。





では、ＡＤを求めていきましょう。

(1)の時と同じく、まずはθを求めるために「正弦定理」を使います。

ＡＣ／sinθ＝６

１４−２ｘ＝６sinθ

sinθ＝７−ｘ／３

ここから、sinθ＝ＡＤ／ＡＢ　に代入します。

７−ｘ／３＝ＡＤ／ｘ

ＡＤ＝ー１／３ｘ^２＋７／３ｘ　となります。





最後にADの取り得る最大値を求めましょう。

ｘの範囲は、４≦ｘ≦６　の範囲

�@４の場合、ＡＤ＝−１６／３＋２８／３＝１２／３＝４
�A６の場合、ＡＤ＝ー１２＋１４＝２

というわけで、最大値は　４　となります。

今回も読んでいただきありがとうございます。
次回以降もよろしくお願いいたします。