2024年05月02日
数学I・A 過去問を丁寧に解説【第4回】
では、引き続き大学入学共通テストを解いていこうと思います。


今回は問題を貼り付けさせていただきます。
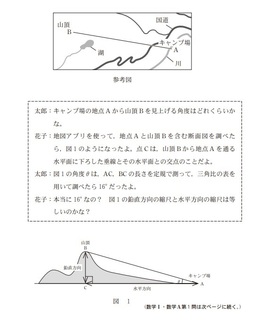

これは、単純な三角関数の問題ですね。


まず、太郎の話から、ACとBCを図ったということが分かります。
そして∠BACの角度は16°であったことも。
この条件を利用すると、tan∠BAC=BC/AC=tan16°=0.2867(三角比の表より)
になります。


ただし、その後に縮尺の条件が追加されており、それを加味すると
tan∠BAC=25000BC/100000AC=BC/4AC が実際の数値になるわけです。
なので実際のtan∠BACは、
1/4 × 0.2867 = 0.071675
この問いの答えでは小数点第三位まで求めることになっているので、0.072が答えになります。


さて、次はこの求めた実際の大きさがどの程度のものかを調べるっ必要があります。
0.072は三角比の表から、tan4°(0.0699)よりも大きくtan5°(0.875)よりも小さいです。
よって、答えは②となります。
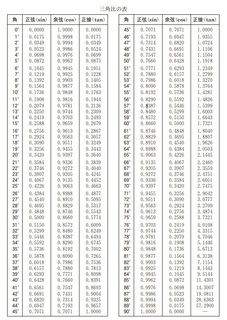
三角比あたりから数学が嫌いになる人も多いと思いますが、理解してしまえば簡単です。
そういった方に少しでもお力になれるよう、今後とも毎日更新頑張ります。

今回は問題を貼り付けさせていただきます。


これは、単純な三角関数の問題ですね。
まず、太郎の話から、ACとBCを図ったということが分かります。
そして∠BACの角度は16°であったことも。
この条件を利用すると、tan∠BAC=BC/AC=tan16°=0.2867(三角比の表より)
になります。
ただし、その後に縮尺の条件が追加されており、それを加味すると
tan∠BAC=25000BC/100000AC=BC/4AC が実際の数値になるわけです。
なので実際のtan∠BACは、
1/4 × 0.2867 = 0.071675
この問いの答えでは小数点第三位まで求めることになっているので、0.072が答えになります。
さて、次はこの求めた実際の大きさがどの程度のものかを調べるっ必要があります。
0.072は三角比の表から、tan4°(0.0699)よりも大きくtan5°(0.875)よりも小さいです。
よって、答えは②となります。

三角比あたりから数学が嫌いになる人も多いと思いますが、理解してしまえば簡単です。
そういった方に少しでもお力になれるよう、今後とも毎日更新頑張ります。
【このカテゴリーの最新記事】
-
no image
-
no image
-
no image
この記事へのコメント
コメントを書く
この記事へのトラックバックURL
https://fanblogs.jp/tb/12532869
※ブログオーナーが承認したトラックバックのみ表示されます。
この記事へのトラックバック