2017�N03��11��
����𗝉����邽�߂̂R�̃X�e�b�v�b�P�ʗʓ�����̑傫��(�T�N��)
�V�����T�C�g�ցb�}�}�Z
�T�C�g�������ǂ݂ɂ����̂ŁA�T�C�g���������ړ����Ă����܂��B��������������������B
�w�N�ʖڎ��y�[�W��
�����ł́A���̏��w�Z���t�Ƃ��Ă̌o���������Z���w���̃|�C���g�����`�����Ă��܂��B
�Z���̋������ŔY�ރ}�}�����̏����ł����ɗ��Ă�Ǝv���Ă��܂��B
�����āA�Z���������Ɗy���ނ��q����ƁA�������̕����������炢���ȂƁB
�����v���ɁA�Z�������Ȏq�͂������A�N�ł��A�Z����g�߂Ɋ�����ꂽ��A�����ƎZ�����y���߂��Ȃ����Ȃƍl���Ă��܂��B
�Z���̃A���e�i�͂�����ƍ������邾���ŁA�Z�����g�߂Ɉ��Ă��邱�ƂɋC�t����̂ł����E�E�E�܂��̓A���e�i���������邫�������Ƃ��āA���͖{��������Ȃ����ȂƎv���Ă��܂��B
���̂�������
�����̖`���V���[�Y �@�n���
�@�n��� �@���
�@��� �@�C��
�@�C�� �@��R��
�@��R��
�Z���̊G�{�͂܂��܂���������܂���I

�P�D����𗝉�����P�ԑ�ȃ|�C���g�́H
�Q�D�ł��Ă����ɂȂ��Ă܂��H
�R�D�X�e�b�v�P�@�܂��͑����Ĕ�r�������Ǝv������
�S�D�X�e�b�v�Q�@�����Ĕ�r�ł��邱�Ƃ̗���
�T�D�X�e�b�v�R�@���Z�̊Ȍ�����m��
�U�D���Z�łP�������߂��闝�R
�V�D����𗝉�����S�̃|�C���g
���R�͔����ɂ�����m�肽�����́�����ĉ���
����̃|�C���g��
��ǂ��炩�ɑ����Ĕ�r����
�Ƃ������Ƃł��B
��ǂ���������ł��܂����H�
�ƕ�����āA�l������������I�ׂ������Ƃ����A
�L����������Ⴄ�������킯�ł���ˁB
�����ŁA�����ł̔�ו��͂Q������A
�E�l���𑵂��āA�L���Ŕ�r����
�E�L���𑵂��āA�l���Ŕ�r����
�̂悤�ɂ�����ƍH�v����Δ�ׂ������Ƃ����P���ł��B
���ڎ���
�Ⴆ����Ȗ��
A:5�u�̂����������ɂW�H
B:4�u�̂����������ɂU�H
�ǂ��炪����ł��܂����H
��l�Ȃ�A�v�͐l�����x�Ɠ���������c
8÷5=1.6
6÷4=1.5
����.A�̕�������ł���
�ƁA�����ɂ��Z�ʼn����ł���ł��傤�B
���q����������悤�ɂł��邩������܂���B
�ł��A�ǂ�����A�Ȃ̂����Е����Ă݂܂��傤�B
�����1�u(�L��)�Ȃ�A���������������ł���(����)����
�Ǝ����悤�ȓ����Ȃ���v���Ǝv���܂��B
�������A
�u�傫������B�v
�̂悤�ɓ������B���Ȏ��Ȃǂ͂���ɁA
�ǂ����Đ������傫���ƍ���ł���̂��H
���Z�ɂ��Čv�Z����Ƃǂ��Ȃ邩�H
���Њm�F�������������Ǝv���܂��B
���̒P���ŁA
�u�����炭���Z���Čv�Z����낤���ǁA�����̈Ӗ����Č����Ă��c�B�v
�Ƃ������q���������܂����B
�v�Z�͂ł��Ă���̂ɔ���I��ł��܂��ĊԈ���Ă��邱�Ƃ�����ꍇ�A��x�m���߂Ă݂�����������������܂���B
���ڎ���
���Z�ʼn������邱�Ƃ�������O�ɁA�܂���
�Е��������Ă���Δ�ׂ���
�Ƃ������Ƃ𗝉����邱�Ƃ���ł��B
�ł�����A
C:4�u�̂�����������5�H
�Ƃ���C�̏���������Ƃ��āA�uB��C�ǂ���������ł�?�v
�ƕ����Ă݂Ă��������B
B��C�Ȃ�AB�̕�������ł��邱�Ƃ�������Ǝv���܂��B
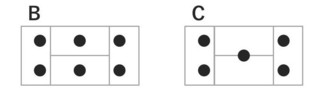
��������A
�u�L���������������番����̂ɂ˂��E�E�E�v
�ƂԂ₭�̂ł��B
���ڎ���
�����Ŏ��ɁA
�u�L�����ɂ��čl���邱�Ƃł���˂��I�v
�ƂЂ�߂����悤�Ȋ����łԂ₢�Ă݂܂��傤�B
�����āA
�u�ǂ����20�u�ɑ��z�����I�v
�ƁB
�u�������������悤�ɑ��₹����͕ς��Ȃ��ł���I�H�Q�O�u�Ȃ�A�������͉��H�ɂȂ�H�v
�ƕ����Ă݂܂��傤�B
A�́@20÷5=4
�܂菬���S���ƍl���A�������́@8×4=32(�H)
B�́@20÷4=5
�܂菬���T���ƍl���A�������́@6×5=30(�H)
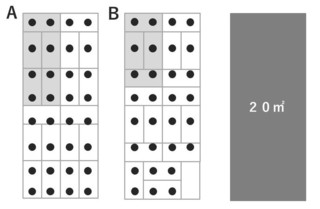
���̂悤�ɍl�����
����20�u�Ł@A��32�H�@B��30�H
A�̕�������������ł����Ȃ̂�������܂��ˁB
���̒P���ł������Ă��������|�C���g�́A
�Е��𑵂��Ĕ�r����
�Ƃ������Ƃł��B
�u�L���͑����邱�Ƃ��ł���ˁI�v
�ƁA�����ĂȂ��Ȃ瑵���Ă��܂��������Ƃ��w�т܂��B
���ڎ���
�ł́A�ǂ�����đ�����̂��ȒP���Ƃ������ƂɂȂ�܂��B
��L�̏ꍇ�A
�@4��5�̍ŏ����{�������߂�
�A���{���邩���߂�
�B�������̐������{����
�菇�Ƃ��Ă͂R�K�v�Ȃ̂��l�b�N�ł��B
�����ŁA���Z�����p����킯�ł��B
���Z�Ȃ�A
�@���Z������
�Ȃ�Ǝ菇���P��ōςނ̂ł��B
�Ȃ����Z�Ȃ�P��ōςނ̂��Ƃ����ƁA
�P�������߂��邩��
�ł��B
�ǂ�����P�u��������H
�ƍl����Ƃ������Ƃł��B
�ǂ�����P�ɂȂ�Ƃ������Ƃ́A
���̒P���̃|�C���g�ł���
�Е��ɑ�������
�Ƃ������Ƃł��B
����Ƃ��Z�̑����͔��Q�Ȃ�ł��ˁB
���ڎ���
���Z�̂P���𗝉����邽�߂ɂ́A
�Q�N���̂����Z�̊w�K�����ɂȂ�܂��B
�Q�N���ňȉ��̂悤��
(�P��)×(������)=(�S���̐�)
�Ƃ����Z�̈Ӗ��̊w�K�����܂��B
�P���Ƃ����ƗႦ�A
�E�P�l��5�����܂莆���@�c�@�P�l��
�E�P�M��2���̃N�b�L�[���@�c�@�P�M��
���̂T��Q���P���Ƃ������Ƃł��B
���ɁA��������ɂR�N����
�@(�S���̐�)÷(�P��)=(������)�@[���]
�A(�S���̐�)÷(������)=(�P��)�@[������]
�Ƃ��Z�̈Ӗ����Q���邱�Ƃ��w�K���܂��B
�A���݂Ă���������Ε�����悤�ɁA���Z�͂P�������߂���̂ł��B
8÷5=1.6
���l���Ă݂܂��傤�B
����̏ꍇ�͇A�̂��Z�����Ă͂܂�܂��B
(�S���̐�)�������͑S���łW�H����Ƃ�������
(������)�T��[�u]�ŕ�����Ƃ�������
�T�����������Z�̓���1.6�͂P���ł���A
(�P��)�P��[�u]��1.6�H�ɂȂ�Ƃ�������
����
5÷8=0.625
�����l�ɁA�A�̂��Z�����Ă͂܂�܂��B
(�S���̐�)�S���łT��[�u]����Ƃ�������
(������)�W�H�ŕ�����Ƃ�������
�W�����������Z�̓���0.625�͂P���ł���A
(�P��)�P�H��0.625��[�u]���炦��Ƃ�������
�J��Ԃ��ɂȂ�܂����A
���Z������A�P�������߂���
�Ƃ������ƂȂ̂ł��B
���ڎ���
���̏͂̂����������|�C���g��������x��������ƁA
�E�Е��ɑ����Ĕ�r���邱��
�E���Z���Ȍ��ɑ������邱��
�E���Z�̏��Ԃ��������Ă���r�ł��邱��
�E�Ȃ炵�čl���邱��
�S�ڂɂ��ĕ⑫���Ă����ƁA
���͑O��Ƃ��Ă������Ă��������d�v�Ȃ��Ƃ��Ǝ��͎v���܂��B
�������������悤�ł����A
�@�����̊p�ɂ��������W�܂��Ă������ł���Ɗ�����̂ł́H
�AB�̏����̂������݂͂�ȑ傫�������狷��������̂ł́H
�Ȃǂƍl�����Ȃ��͂Ȃ��ł���ˁB
�����ŁA��ȑO����m�F�����Ă��������B
�Z���̐��E�͗��z�̐��E�łł��Ă���Ƃ������Ƃł��B
�ł�����A
�E�����̒��ł������͋ϓ��ɎU��邱��
�E�������Ɍ̍��͂Ȃ��A�ǂ̂������������ł��邱��
���O��ƂȂ��Ęb��i�߂邱�ƂɂȂ�̂ł��B
���̂��Ƃ́A������w�K����ŏ��̕��ł����Ɗm�F���Ă����ƁA����������ɃX���[�Y�ɂȂ�Ǝv���܂���B
���ڎ���
���ɒP�ʂ�����������悤�ɂ����Ă��������B
8(�H)÷5(�u)=1.6(�H/�P�u��)
�����̑召�Ɋւ�炸�A�P�ʂ̈ʒu�͕ς��Ȃ����Ƃ�`���Ă��������B
������ς��ĉ����K���Ă݂�ƁA�����ɂł���Ǝv���܂��B
���������̎��������鉻����H�v�ł��B
����́A(�H)��(�C)�ɕς���Ă�(�l)�ł��Ή��\�ł��B
�������̒P���́A���Z�̏��Ԃ����ւ��Ă���ׂ��邱�Ƃ����߂��܂��B
�ł�����A�������芵�ꂽ�Ȃ�(�ł�Ȃ��ł��������ˁB)�Ǝv����������ŁA
5÷8=0.625
���Ă݂Ă��������B
5(�u)÷8(�H)=0.625(�u/1�H��)
�P�ʂ̏��Ԃ�����ւ�邱�Ƃ��m�F���A
1�H��0.625�u�̈Ӗ��ɂ��ċ�����Ƃ����Ǝv���܂��B
���̈Ӗ��A�v��
���������炦��L��
�ł��ˁB
����������قǍ���ł���Ƃ������ƂŁA
���x�͏���������I�Ԃ��ƂɂȂ�̂ł��B
����Ă������́A���Ԃ�����Η��R�����Гǂ�ł݂Ă��������B��TOP��

������͎Z���E���w����֘A�̃u���O���W�܂��Ă���T�C�g�ł��B
�����ŋ����邱�Ƃ�I���������炵���}�}�ցB
�������Ă��q����ɋ�������̂͂킸�����N�����Ȃ̂͊ԈႢ�Ȃ��ł��B
���̍ہA�e�q�̎��ԂƂ��đ����A��������Ɗy���ނ��Ƃ��������߂��܂��B
������̂ɑ�Ȃ̂͂�Ƃ肾�Ǝv���܂��B
���Ԃɂ��S�ɂ���Ƃ肪����ƁA�e�q�̎��Ԃ͂����ƖL���ŋP�����Ƃł��傤�B
���̃u���O�́A�}�}���Ǝ��̌��Ԃł���������悤�A��̓I�ɁA�����ă|�C���g�����m�ƂȂ�悤�S�����Ă������ł��B
�����͂����Ă���Ƃ�ȂE�E�E�Ƃ������ɂ́A�v�������ĊO���̗͂���Ă��܂��A����Ȏ�����邩������܂���ˁB


���������ƂɔC����̂������ł��傤�B������ɐ\������ł��邲�ƒ�̖�3����2���������̂��ƒ낾�����ł��B������͖Z�������ƒ낪�������炱���A���C�����ςȂ��ɂȂ肪���ȂƂ�����A���q����ƕی�҂̕��̃R�~���j�P�[�V�������ɂ��Ă���悤�ł��B


�ƒ닳�t�̂���A�����̌����b�X�����\���̓R�`��

���ނ�I�Ԃ̂ɍ����Ă���Ȃ�u�ƒ낱���q�ǂ������̕�Z�ł����Ăق����v�Ƃ���������̗��O�́A������}�}�ɂ҂�����ł��B����Θb�����Ƃ��������ŁA�ƒ닳��̂��낢��ȋ^��E���k�ɉ�����d�g�݂�����A�o�b�N�A�b�v���[�����Ă��܂��B


�}�}�̏����ł��菕���ɂȂ�A���q����̖������x���ł�����K���ł��B
���������ł͕�����Ȃ����Ƃ́A�R�����g����������A�ꏏ�ɍl�������Ǝv���܂��B
�w�N�ʖڎ��y�[�W��
�T�C�g�������ǂ݂ɂ����̂ŁA�T�C�g���������ړ����Ă����܂��B��������������������B
�w�N�ʖڎ��y�[�W��
�����ł́A���̏��w�Z���t�Ƃ��Ă̌o���������Z���w���̃|�C���g�����`�����Ă��܂��B
�Z���̋������ŔY�ރ}�}�����̏����ł����ɗ��Ă�Ǝv���Ă��܂��B
�����āA�Z���������Ɗy���ނ��q����ƁA�������̕����������炢���ȂƁB
�����v���ɁA�Z�������Ȏq�͂������A�N�ł��A�Z����g�߂Ɋ�����ꂽ��A�����ƎZ�����y���߂��Ȃ����Ȃƍl���Ă��܂��B
�Z���̃A���e�i�͂�����ƍ������邾���ŁA�Z�����g�߂Ɉ��Ă��邱�ƂɋC�t����̂ł����E�E�E�܂��̓A���e�i���������邫�������Ƃ��āA���͖{��������Ȃ����ȂƎv���Ă��܂��B
���̂�������
�����̖`���V���[�Y
�Z���̊G�{�͂܂��܂���������܂���I
�P�D����𗝉�����P�ԑ�ȃ|�C���g�́H
�Q�D�ł��Ă����ɂȂ��Ă܂��H
�R�D�X�e�b�v�P�@�܂��͑����Ĕ�r�������Ǝv������
�S�D�X�e�b�v�Q�@�����Ĕ�r�ł��邱�Ƃ̗���
�T�D�X�e�b�v�R�@���Z�̊Ȍ�����m��
�U�D���Z�łP�������߂��闝�R
�V�D����𗝉�����S�̃|�C���g
���R�͔����ɂ�����m�肽�����́�����ĉ���
�P�D����𗝉�����P�ԑ�ȃ|�C���g�́H
����̃|�C���g��
��ǂ��炩�ɑ����Ĕ�r����
�Ƃ������Ƃł��B
��ǂ���������ł��܂����H�
�ƕ�����āA�l������������I�ׂ������Ƃ����A
�L����������Ⴄ�������킯�ł���ˁB
�����ŁA�����ł̔�ו��͂Q������A
�E�l���𑵂��āA�L���Ŕ�r����
�E�L���𑵂��āA�l���Ŕ�r����
�̂悤�ɂ�����ƍH�v����Δ�ׂ������Ƃ����P���ł��B
���ڎ���
�Q�D�ł��Ă����ɂȂ��Ă܂��H
�Ⴆ����Ȗ��
A:5�u�̂����������ɂW�H
B:4�u�̂����������ɂU�H
�ǂ��炪����ł��܂����H
��l�Ȃ�A�v�͐l�����x�Ɠ���������c
8÷5=1.6
6÷4=1.5
����.A�̕�������ł���
�ƁA�����ɂ��Z�ʼn����ł���ł��傤�B
���q����������悤�ɂł��邩������܂���B
�ł��A�ǂ�����A�Ȃ̂����Е����Ă݂܂��傤�B
�����1�u(�L��)�Ȃ�A���������������ł���(����)����
�Ǝ����悤�ȓ����Ȃ���v���Ǝv���܂��B
�������A
�u�傫������B�v
�̂悤�ɓ������B���Ȏ��Ȃǂ͂���ɁA
�ǂ����Đ������傫���ƍ���ł���̂��H
���Z�ɂ��Čv�Z����Ƃǂ��Ȃ邩�H
���Њm�F�������������Ǝv���܂��B
���̒P���ŁA
�u�����炭���Z���Čv�Z����낤���ǁA�����̈Ӗ����Č����Ă��c�B�v
�Ƃ������q���������܂����B
�v�Z�͂ł��Ă���̂ɔ���I��ł��܂��ĊԈ���Ă��邱�Ƃ�����ꍇ�A��x�m���߂Ă݂�����������������܂���B
���ڎ���
�R�D�X�e�b�v�P�@�܂��͑����Ĕ�r�������Ǝv������
���Z�ʼn������邱�Ƃ�������O�ɁA�܂���
�Е��������Ă���Δ�ׂ���
�Ƃ������Ƃ𗝉����邱�Ƃ���ł��B
�ł�����A
C:4�u�̂�����������5�H
�Ƃ���C�̏���������Ƃ��āA�uB��C�ǂ���������ł�?�v
�ƕ����Ă݂Ă��������B
B��C�Ȃ�AB�̕�������ł��邱�Ƃ�������Ǝv���܂��B

��������A
�u�L���������������番����̂ɂ˂��E�E�E�v
�ƂԂ₭�̂ł��B
���ڎ���
�S�D�X�e�b�v�Q�@�����Ĕ�r�ł��邱�Ƃ̗���
�����Ŏ��ɁA
�u�L�����ɂ��čl���邱�Ƃł���˂��I�v
�ƂЂ�߂����悤�Ȋ����łԂ₢�Ă݂܂��傤�B
�����āA
�u�ǂ����20�u�ɑ��z�����I�v
�ƁB
�u�������������悤�ɑ��₹����͕ς��Ȃ��ł���I�H�Q�O�u�Ȃ�A�������͉��H�ɂȂ�H�v
�ƕ����Ă݂܂��傤�B
A�́@20÷5=4
�܂菬���S���ƍl���A�������́@8×4=32(�H)
B�́@20÷4=5
�܂菬���T���ƍl���A�������́@6×5=30(�H)

���̂悤�ɍl�����
����20�u�Ł@A��32�H�@B��30�H
A�̕�������������ł����Ȃ̂�������܂��ˁB
���̒P���ł������Ă��������|�C���g�́A
�Е��𑵂��Ĕ�r����
�Ƃ������Ƃł��B
�u�L���͑����邱�Ƃ��ł���ˁI�v
�ƁA�����ĂȂ��Ȃ瑵���Ă��܂��������Ƃ��w�т܂��B
���ڎ���
�T�D�X�e�b�v�R�@���Z�̊Ȍ�����m��
�ł́A�ǂ�����đ�����̂��ȒP���Ƃ������ƂɂȂ�܂��B
��L�̏ꍇ�A
�@4��5�̍ŏ����{�������߂�
�A���{���邩���߂�
�B�������̐������{����
�菇�Ƃ��Ă͂R�K�v�Ȃ̂��l�b�N�ł��B
�����ŁA���Z�����p����킯�ł��B
���Z�Ȃ�A
�@���Z������
�Ȃ�Ǝ菇���P��ōςނ̂ł��B
�Ȃ����Z�Ȃ�P��ōςނ̂��Ƃ����ƁA
�P�������߂��邩��
�ł��B
�ǂ�����P�u��������H
�ƍl����Ƃ������Ƃł��B
�ǂ�����P�ɂȂ�Ƃ������Ƃ́A
���̒P���̃|�C���g�ł���
�Е��ɑ�������
�Ƃ������Ƃł��B
����Ƃ��Z�̑����͔��Q�Ȃ�ł��ˁB
���ڎ���
�U�D���Z�łP�������߂��闝�R
���Z�̂P���𗝉����邽�߂ɂ́A
�Q�N���̂����Z�̊w�K�����ɂȂ�܂��B
�Q�N���ňȉ��̂悤��
(�P��)×(������)=(�S���̐�)
�Ƃ����Z�̈Ӗ��̊w�K�����܂��B
�P���Ƃ����ƗႦ�A
�E�P�l��5�����܂莆���@�c�@�P�l��
�E�P�M��2���̃N�b�L�[���@�c�@�P�M��
���̂T��Q���P���Ƃ������Ƃł��B
���ɁA��������ɂR�N����
�@(�S���̐�)÷(�P��)=(������)�@[���]
�A(�S���̐�)÷(������)=(�P��)�@[������]
�Ƃ��Z�̈Ӗ����Q���邱�Ƃ��w�K���܂��B
�A���݂Ă���������Ε�����悤�ɁA���Z�͂P�������߂���̂ł��B
8÷5=1.6
���l���Ă݂܂��傤�B
����̏ꍇ�͇A�̂��Z�����Ă͂܂�܂��B
(�S���̐�)�������͑S���łW�H����Ƃ�������
(������)�T��[�u]�ŕ�����Ƃ�������
�T�����������Z�̓���1.6�͂P���ł���A
(�P��)�P��[�u]��1.6�H�ɂȂ�Ƃ�������
����
5÷8=0.625
�����l�ɁA�A�̂��Z�����Ă͂܂�܂��B
(�S���̐�)�S���łT��[�u]����Ƃ�������
(������)�W�H�ŕ�����Ƃ�������
�W�����������Z�̓���0.625�͂P���ł���A
(�P��)�P�H��0.625��[�u]���炦��Ƃ�������
�J��Ԃ��ɂȂ�܂����A
���Z������A�P�������߂���
�Ƃ������ƂȂ̂ł��B
���ڎ���
�V�D����𗝉�����S�̃|�C���g
���̏͂̂����������|�C���g��������x��������ƁA
�E�Е��ɑ����Ĕ�r���邱��
�E���Z���Ȍ��ɑ������邱��
�E���Z�̏��Ԃ��������Ă���r�ł��邱��
�E�Ȃ炵�čl���邱��
�S�ڂɂ��ĕ⑫���Ă����ƁA
���͑O��Ƃ��Ă������Ă��������d�v�Ȃ��Ƃ��Ǝ��͎v���܂��B
�������������悤�ł����A
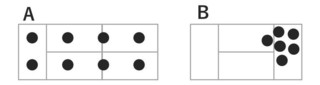
�@�����̊p�ɂ��������W�܂��Ă������ł���Ɗ�����̂ł́H

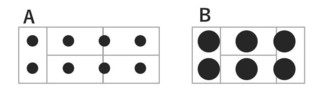
�AB�̏����̂������݂͂�ȑ傫�������狷��������̂ł́H

�Ȃǂƍl�����Ȃ��͂Ȃ��ł���ˁB
�����ŁA��ȑO����m�F�����Ă��������B
�Z���̐��E�͗��z�̐��E�łł��Ă���Ƃ������Ƃł��B
�ł�����A
�E�����̒��ł������͋ϓ��ɎU��邱��
�E�������Ɍ̍��͂Ȃ��A�ǂ̂������������ł��邱��
���O��ƂȂ��Ęb��i�߂邱�ƂɂȂ�̂ł��B
���̂��Ƃ́A������w�K����ŏ��̕��ł����Ɗm�F���Ă����ƁA����������ɃX���[�Y�ɂȂ�Ǝv���܂���B
���ڎ���
�W�D���R�͔����ɍ��������������@
���ɒP�ʂ�����������悤�ɂ����Ă��������B
8(�H)÷5(�u)=1.6(�H/�P�u��)
�����̑召�Ɋւ�炸�A�P�ʂ̈ʒu�͕ς��Ȃ����Ƃ�`���Ă��������B
������ς��ĉ����K���Ă݂�ƁA�����ɂł���Ǝv���܂��B
���������̎��������鉻����H�v�ł��B
����́A(�H)��(�C)�ɕς���Ă�(�l)�ł��Ή��\�ł��B
�������̒P���́A���Z�̏��Ԃ����ւ��Ă���ׂ��邱�Ƃ����߂��܂��B
�ł�����A�������芵�ꂽ�Ȃ�(�ł�Ȃ��ł��������ˁB)�Ǝv����������ŁA
5÷8=0.625
���Ă݂Ă��������B
5(�u)÷8(�H)=0.625(�u/1�H��)
�P�ʂ̏��Ԃ�����ւ�邱�Ƃ��m�F���A
1�H��0.625�u�̈Ӗ��ɂ��ċ�����Ƃ����Ǝv���܂��B
���̈Ӗ��A�v��
���������炦��L��
�ł��ˁB
����������قǍ���ł���Ƃ������ƂŁA
���x�͏���������I�Ԃ��ƂɂȂ�̂ł��B
����Ă������́A���Ԃ�����Η��R�����Гǂ�ł݂Ă��������B��TOP��
������͎Z���E���w����֘A�̃u���O���W�܂��Ă���T�C�g�ł��B
�W�D�}�}�ɂ͂�Ƃ��
�����ŋ����邱�Ƃ�I���������炵���}�}�ցB
�������Ă��q����ɋ�������̂͂킸�����N�����Ȃ̂͊ԈႢ�Ȃ��ł��B
���̍ہA�e�q�̎��ԂƂ��đ����A��������Ɗy���ނ��Ƃ��������߂��܂��B
������̂ɑ�Ȃ̂͂�Ƃ肾�Ǝv���܂��B
���Ԃɂ��S�ɂ���Ƃ肪����ƁA�e�q�̎��Ԃ͂����ƖL���ŋP�����Ƃł��傤�B
���̃u���O�́A�}�}���Ǝ��̌��Ԃł���������悤�A��̓I�ɁA�����ă|�C���g�����m�ƂȂ�悤�S�����Ă������ł��B
�����͂����Ă���Ƃ�ȂE�E�E�Ƃ������ɂ́A�v�������ĊO���̗͂���Ă��܂��A����Ȏ�����邩������܂���ˁB
���������ƂɔC����̂������ł��傤�B������ɐ\������ł��邲�ƒ�̖�3����2���������̂��ƒ낾�����ł��B������͖Z�������ƒ낪�������炱���A���C�����ςȂ��ɂȂ肪���ȂƂ�����A���q����ƕی�҂̕��̃R�~���j�P�[�V�������ɂ��Ă���悤�ł��B
�ƒ닳�t�̂���A�����̌����b�X�����\���̓R�`��
���ނ�I�Ԃ̂ɍ����Ă���Ȃ�u�ƒ낱���q�ǂ������̕�Z�ł����Ăق����v�Ƃ���������̗��O�́A������}�}�ɂ҂�����ł��B����Θb�����Ƃ��������ŁA�ƒ닳��̂��낢��ȋ^��E���k�ɉ�����d�g�݂�����A�o�b�N�A�b�v���[�����Ă��܂��B
�}�}�̏����ł��菕���ɂȂ�A���q����̖������x���ł�����K���ł��B
���������ł͕�����Ȃ����Ƃ́A�R�����g����������A�ꏏ�ɍl�������Ǝv���܂��B
�w�N�ʖڎ��y�[�W��
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
-
no image
-
no image
���̋L���ւ̃R�����g
�R�����g������
���̋L���ւ̃g���b�N�o�b�NURL
https://fanblogs.jp/tb/6036391
���u���O�I�[�i�[�����F�����g���b�N�o�b�N�̂ݕ\������܂��B
���̋L���ւ̃g���b�N�o�b�N



