投資関係のことをアウトプット

こんばんは，kanatoです．
寒さの厳しい日が続いていますが，いかがお過ごしでしょうか．
うちでは最近新しい羽毛布団を買って，暖かく寝れるようになりました．
また，昨日の雇用統計ではサプライズでしたね．
ほとんどのEAは一旦停止していたので，大きな影響は無かったのですが・・・

さて，本日から時々，テクニカル分析について書いてみたいと思います．
っといいますのも，トレードやEAを作成する上で色々なテクニカル分析を使っていますが，
自分自身，その意味を把握し切れていないように感じてましたので・・・．

以降，スポットを当てたテクニカル分析について，計算方法やその指標の意味する事，
大まかなトレード戦略などをまとめていきたいと思います．

本日は最初ということで，最もメジャーなテクニカル分析である
移動平均線にスポットを当てたいと思います．

移動平均線は，相場の世界に入って多くの人が
最初に出会うテクニカル分析ではないでしょうか．

このテクニカル分析手法はトレンド系指標に分類され，
大まかに言うと「直近の一定期間のレートの平均」を見ています．
計算に使われるレートは一般的に終値が使われていますが，
始値や高値と安値の平均を使うこともあります．
また，10日間移動平均や25本移動平均などと呼ばれることが多いと思います．
前者は直近10日間（当日含む）の移動平均，
後者は直近25本のローソク足等の移動平均を指しています．

計算式は次のようになります．

n本移動平均＝(P1+P2+P3+･････+Pn)／n
　P1=現在から1本目のレート
　Pn=現在からn本目のレート

なお，通常の移動平均は単純に一定期間のレートの平均を取っていることから「単純移動平均(SMA)」と呼ばれることが多いと思います．
日本国内ではこのSMAが多く使われているようです．

しかし，単純移動平均では単純な算出方法のため，
時間軸が考慮されていなかったり（古い情報より新しい情報のほうが重要度が高い），
指定した本数のレート以前の情報は一切考慮されていません（たとえ直前で○○ショックがあっても・・・）．

そういった点を補うために改良されたのが加重移動平均（WMA）や
指数移動平均（EMA）です．

それぞれの計算式は次のとおりです．

n本加重移動平均（WMA）= (P1×n+P2×(n-1)+P3×(n-2)+･････+Pn×1)／(n+(n-1)+(n-2)+･････+1)　
加重のかけ方にも種類があり，上記は線形加重移動平均（LWMA）と呼ばれるものですが，他にも三角関数のsinを利用した正弦加重移動平均（SWMA）などもあります．

指数移動平均（EMA）= EMA[prev]＋α(P1-EMA[prev])　
　EMA[prev]=1本前のEMA
　（データの先頭からN本目のデータから計算を始めますが最初のEMAは単純移動平均を使います．）
　α：平滑化係数 = 2/(N+1)
　N：時系列区間
　αを1/Nとすると平滑移動平均（SMMA）になります．


線形加重移動平均（LWMA）は現在値から離れるほど比重が小さくなっていきます．
指数移動平均も同様に古いレートほど比重が小さくなりますが，指数関数的に減少していくことで，
より直近のレートにウエイトを置きつつも，古いレートもしっかりと全て織り込んでることが特徴です．
（ちなみに直近N日間のデータがEMAにおいて，およそ86%の重みを持ちます．）
このことで先にあげた単純移動平均の弱点を軽減できています．
また，直近のレートを重要視することから，レートの変動に敏感に反応するため，
欧米では移動平均線というとEMAが主流との見方もあるようです．

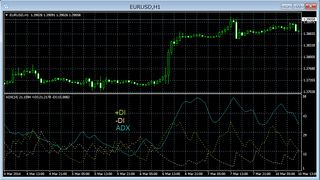
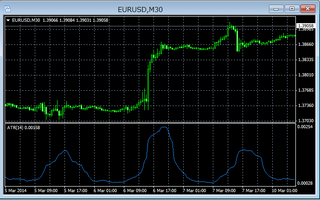
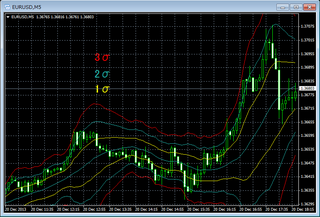
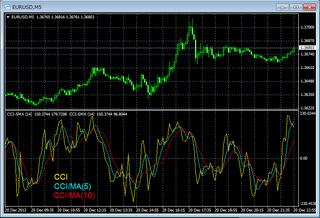
上記の移動平均線をチャートに表示させると
このようになります．



今回は移動平均線の中でも比較的メジャーなものの計算方法をまとめてみました．
次回はこれら移動平均線が持つ特徴や意味についてまとめたいと思います．

本日も最後までお付き合いいただき，ありがとうございます．