Python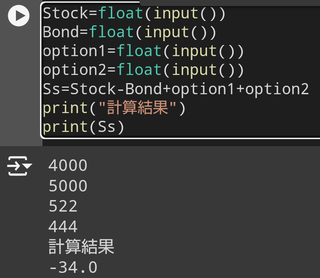


�����̗\���ɂ��Ă�
��ʓI�� ���m�I�Ȃ����ɂ��Č�����
1962�N���ł� �x�[�^�l�Ƃ����̂�
���̒��S�ɂȂ��Ă��܂���
�x�[�^�l�̒l�� ��ʓI�ɕ��ϊ����Ǝ��{���v�����Q�l�ɂ��ďo����܂�
���̂����͗��_�I�ł͂���܂���
���ϊ����͑�� �M���ł���f�[�^�ł����ǂ�
���{���v���ɂ��Ă� ���܂������Ǝv���� ���܂�����Ƃ������Ƃ����̂��� �f�[�^�̐M���x�ɋ^������l�������Ă��܂���
���̂��� ����ɑ�����
��蕪�̗\����s��
�I�v�V�������i�̃{���e�B���e�B��
���{���v���ɕς���ĐM����悤��
�����
�M�͊w �`�� �������Ɍ�����
���S�Ɍ��藝�Ɋ�Â� �l��
���ϊ����̖������ʂ���
��s�ɂ���Ă��̒��œ����� ��������
�x�[�^�l�̒l����̑�����ʂ����Ƃ���������������܂���
������ ��s�̖����ɂ��Ă�
�K�̗͂��v�Ƃ����ϓ_����
���E�����邱�Ƃ��m����悤�ɂȂ�܂���
���̕��@�ɂ�������x�̌��E�����邱�Ƃ��w�E�����悤�ɂȂ��Ă��܂�
�����̗\���Ƃ����ϓ_�ɂ��Ă�
���݉��l�Ƃ����ϓ_����
�A�v���[�`�����݂���@��
��Ă����Ă������������Ǝv���܂�
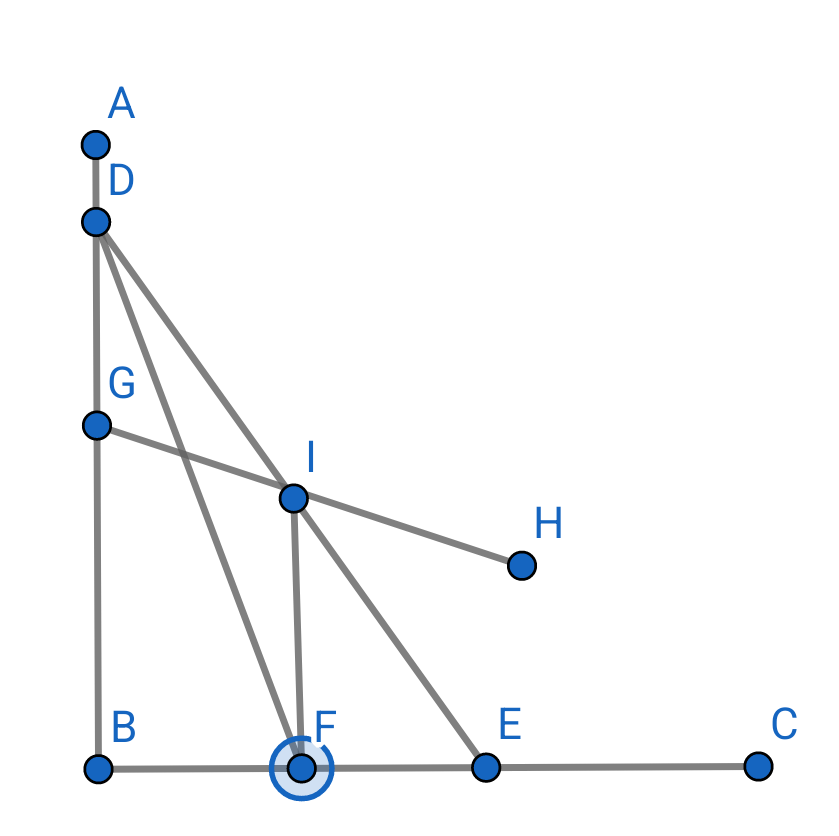
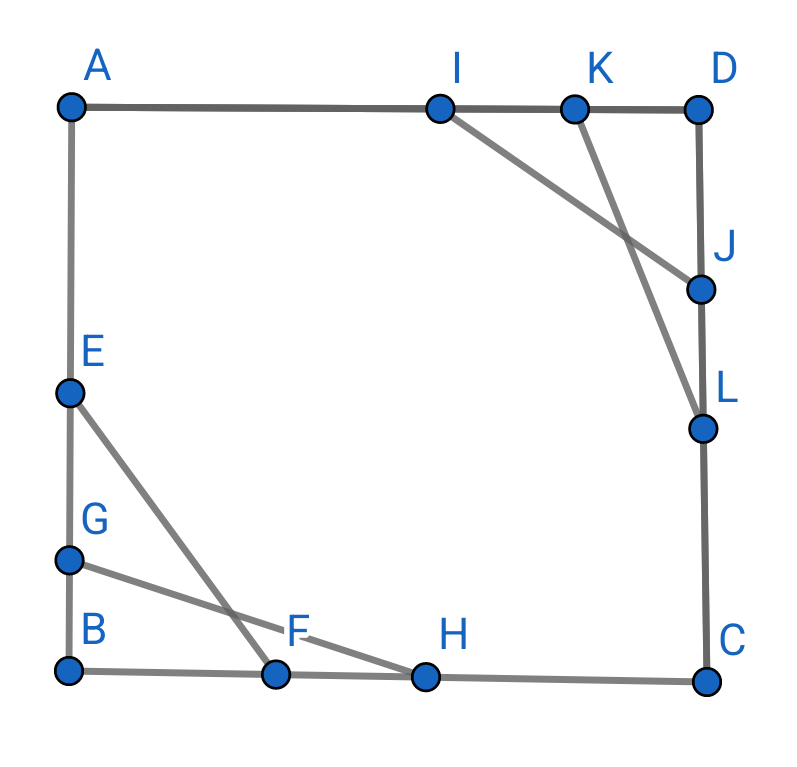
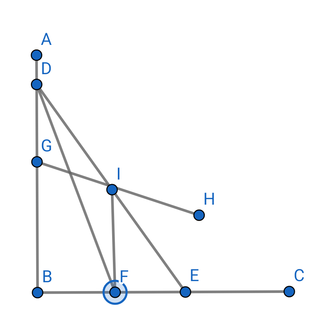
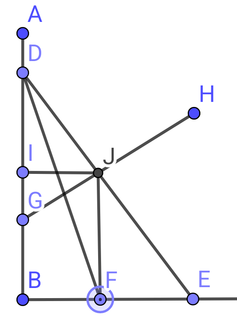
���� �z�u�}����
��
SOS �����̉��i�Ƃ���ɑΉ�����I�v�V�������i�̓��͂����ė\�z�����l�������͍��ڂɂȂ�܂� ����Ɋւ��銔���̗\�z�ɂ��Ă�
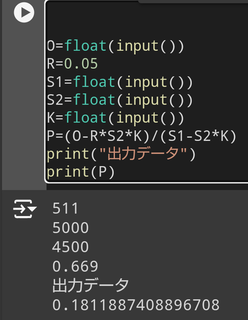
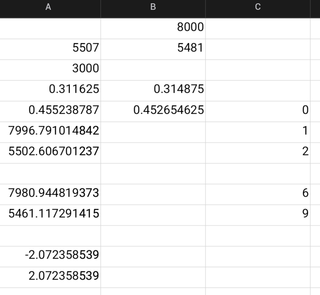
4�̒l���o��
����ɂ���Ė��� �z�u�}�ʂ��\�����邱�Ƃ��\�ł�
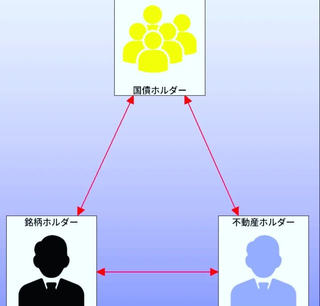
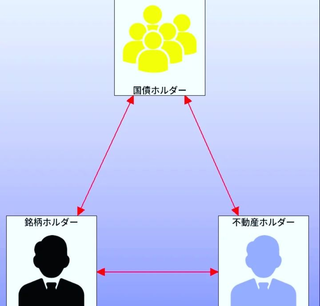
�f�[�^���o�͂���� �t�H���[�Ƃ��Ă�
�@�\�z�����l����z�肵�܂�
�A����ɑΉ�����I�v�V�������i��z�肵�܂�
�B�܂��ŏ��Ɍ��݉��l�̃|�W�V�����̒l���o�͂���܂�
�C����ɑΉ�����l�����o�͂���܂�
�ŏ��ɑz�肵���l���ɋ߂��f�[�^���o�͂���邱�Ƃ��]�܂����ł��傤
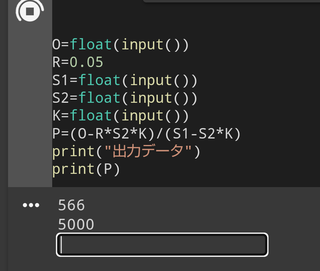
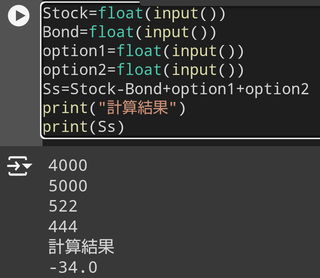
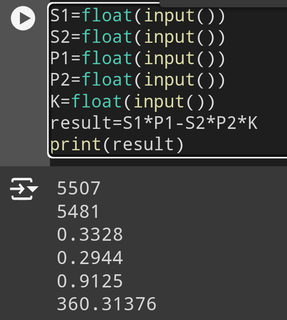
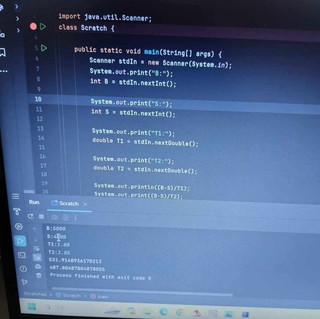
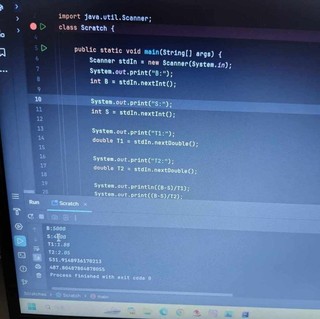
�ŏ��Ɍf�ڂ��Ă���摜�ɂ��ĊȒP�Ȑ����������Ă��������܂�
�悭�m���� Python �̃v���O�����ł������܂�
���{�̃r�W�l�X�}���� Python ���悭�g���Ă���Ƃ������Ƃ��m���Ă��� ���ɓ��{�̃r�W�l�X�}���̓A�i�R���_���g���Ă���Ƃ������Ƃł�
������ �����ŏЉ���Ă��������Ă���̂�
�R���{�̃p�C�\���ł������܂�
��`�L��