2024年11月17日
有価証券の経済モデル
経済モデル1
広告宣伝


SOS
経済モデル1
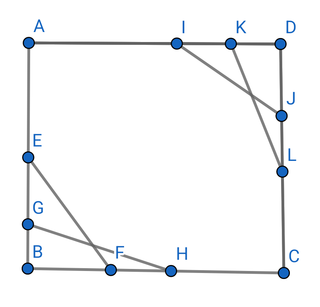
双方独占のモデル
この場合 独占価格を使用する企業が2つあり
GH→LK
一方の銘柄の価格が下がれば一方の企業の銘柄の価格は上がります また銘柄を保有する 所有者も一方の所有者が増えることで 一方の所有者は減少するという関係が成立します
人数の減少によって起こる銘柄の価格の変動は表示 計算方式 これによって 想定することが可能です
LK 例えばこの部分の直線を曲線化することによって価格 独占モデルの平均費用を構成することができます
経済モデル2
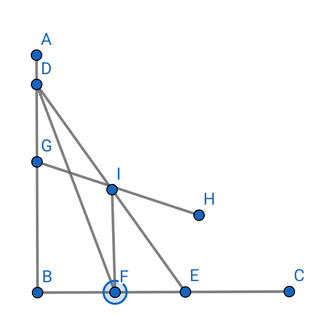
経済モデル2
独占価格を使用する企業のモデルになりますが
DE→DF
需要曲線と収入曲線が組み合わさっています
FE
証券市場のオプション価格は独占価格の一種でありますが
オプションが行使されたことによって
リリース後の
自由な価格が発生することに
この部分については 独占価格の影響は受けず
完全な自由市場として
オプションから解放された
証券市場のマーケットになります
この場合の
市場占有率を考慮に入れた
モジュラー形式の方程式を
S*(DE)-S*(DF)*Exp=option
この計算を形式ではなく実装することは
タップによる計算によって可能です
この計算が前提条件は 公的債権である 国債から銘柄を差し引いた部分
これに バロメーターによって調整するとオプション価格が
独占的な価格と自由市場
これを調整していると見ることができます
SOS
資産の多くは富裕層が80%を握っていると言われています すると残りの20%を一般の投資家が分配を受けていることになります また 富裕層は投資家の中で20%であるというのが一般的であると言われています
↓
↓
↓
財産は100%
人数はパーセントを使って調整しています
経済モデル3
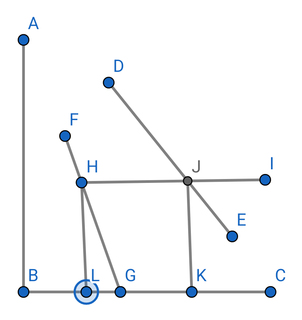
このモデルでは
HJ
これが 曲線化することが可能です
これは経済モデル1に見られる
直線の部分をシフトさせ 曲線化することによって得ることができます
L→K
証券市場の細分化によって
有価証券の需要が増え
有価証券の所有者が増加することになります
全体として 銘柄が入手しやすい状態になります
その際にかかるコストは
平均費用という形で
独占的な企業が コスト負担している形になります
宣伝広告



広告宣伝
経済モデル1
双方独占のモデル
この場合 独占価格を使用する企業が2つあり
GH→LK
一方の銘柄の価格が下がれば一方の企業の銘柄の価格は上がります また銘柄を保有する 所有者も一方の所有者が増えることで 一方の所有者は減少するという関係が成立します
人数の減少によって起こる銘柄の価格の変動は表示 計算方式 これによって 想定することが可能です
LK 例えばこの部分の直線を曲線化することによって価格 独占モデルの平均費用を構成することができます
経済モデル2

経済モデル2
独占価格を使用する企業のモデルになりますが
DE→DF
需要曲線と収入曲線が組み合わさっています
FE
証券市場のオプション価格は独占価格の一種でありますが
オプションが行使されたことによって
リリース後の
自由な価格が発生することに
この部分については 独占価格の影響は受けず
完全な自由市場として
オプションから解放された
証券市場のマーケットになります
この場合の
市場占有率を考慮に入れた
モジュラー形式の方程式を
S*(DE)-S*(DF)*Exp=option
この計算を形式ではなく実装することは
タップによる計算によって可能です
この計算が前提条件は 公的債権である 国債から銘柄を差し引いた部分
これに バロメーターによって調整するとオプション価格が
独占的な価格と自由市場
これを調整していると見ることができます
資産の多くは富裕層が80%を握っていると言われています すると残りの20%を一般の投資家が分配を受けていることになります また 富裕層は投資家の中で20%であるというのが一般的であると言われています
↓
↓
↓
財産は100%
人数はパーセントを使って調整しています
経済モデル3

このモデルでは
HJ
これが 曲線化することが可能です
これは経済モデル1に見られる
直線の部分をシフトさせ 曲線化することによって得ることができます
L→K
証券市場の細分化によって
有価証券の需要が増え
有価証券の所有者が増加することになります
全体として 銘柄が入手しやすい状態になります
その際にかかるコストは
平均費用という形で
独占的な企業が コスト負担している形になります
宣伝広告
【このカテゴリーの最新記事】
この記事へのコメント
コメントを書く
この記事へのトラックバックURL
https://fanblogs.jp/tb/12783336
※ブログオーナーが承認したトラックバックのみ表示されます。
この記事へのトラックバック