広告宣伝
オプションを調整役として 銘柄と銘柄の交換能力を高めるための計算書の構成になります

ⅯⅯⅯ
(経済モデル1-1)
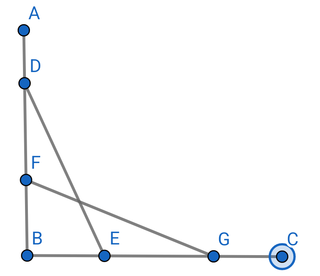
AG→DE
AD→FG
経済モデルから経済モデルへ 次のようなシフトを描いてみます
DE
FG
これが経済モデルの(経済モデル1-1)
市場が独占的部分と自由市場の部分に分かれておりますのでそれをそのまま 損失と利益の部分に分けるという形になり 2等分 という前提条件に変更はありません
まずマーケティング シェアが狭いところで
オプションが1つ 存在しているという 想定になります
マーケティング シェアが広がったら オプションが消えてしまうという性質のものではないのでここでも オプションが存在するという前提条件に立ちます
この事実を単純に受け入れる
その結果として
(S1-S2)/T=オプション価格
この極めて単純な性質が想定されると言えます

AG→AD
計算書に見られるモデルの
前提条件は
経済モデルの中に見られる限界 需要曲線と限界収入要素 曲線のシフトにあります
EFG
経済モデルの中に示される この領域の中に独占的な企業が 価格設定をする可能性があります
F
縦軸に価格を取った場合 このF ここが価格となります
横軸に マーケティング シェアを取った場合
価格が限りなくゼロに近づくまで
市場拡大し続けると考えた場合
限界に達するまで マーケティング シェアを伸び続け 価格 ゼロのところで需要曲線は限界に達することになります
①BG→GD
独占的な企業と一般的な企業が市場を二等分していると想定しますと
BG
この領域が独占的な企業のマーケティング シェアになります
GD
こちらが一般的な企業のマーケティング シェアになります
価格競争力という観点からは一般的な企業は
F
この地点より低い価格を設定せざるを得なくなります
②この問題を オプションという問題に置き換えた時に
BG
これが最初に設定される オプション価格で独占的であれば 強気相場のコールオプションになるはず
GD
オプションは 証券市場の中で独占価格の一種ですから この領域を除けば
そこからは オプションから解放された領域になります
仮に2つの領域が関連していると考えると
このオプションを構成するために使われている
価格は
BG(S1)-GD(S2)*exp=option
形式的にはこのような構成が可能になります
(経済モデル1-1)
③実際の計算書は2等分 というところを重視していますので画面にも見られるように
2等分した結果の一方を利益 一方を損失と見ています
マーケティング シェアにおける2等分 という考え方を実際の利益と損失という分け方にシフトさせたものです
したがって 指数として 3以上のパラメーターが選択された場合 警告が出る場合がございますのでよろしく ご注意いただければありがたく存じます
ここまでの説明は(経済モデル1-2)
これを利用させていただいております
④ここからの説明は (経済モデル1-1)
ⅯⅯⅯ
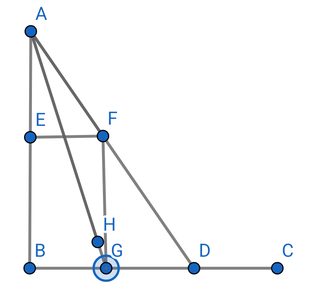
(経済モデル1-2)
価格の動向とマーケティング シェアの動向をそれぞれstrong weak 2つの観点から見たような場合SS SW WS WW 価格をマーケティング シェアも極めて同じ性質を持つ場合と正反対になる場合とはあるということになります
1 SS
2 SW
3 WS
4 WW
①BG→GD
BG-GD*exp=O
BG*exp-GD=O
証券市場の価格を銀行の金利で限りなく 割引いていけばその価値は消滅してしまいます
BG=O
その結果 オプションと株価が等しいということになってしまいます しかしこれは現実的ではありませんが 先ほど紹介させていただいた限界 需要曲線という考え方から行くと理論値としては否定できません
GD=-O
オプションがマイナスの値を取り
銘柄のコストという側面があることを考えると 一見して現実 のように見えるのは こちらの方です
②この結果を整理しますと
BG=O
GD=-O
BG=GD
このように想定しますと
オプション+ オプション=0
このような結果になります
オプションとオプションをたしたものが0になるという結論は
call long+put short=先物商品の購入価格
この方程式から考えて
整合性があることは分かります
③これらを マーケティング シェアの原理 だけを見て考えますと
BG=GD
GB=DG
BG+GD=0
BG-GD=0
これらを言葉で一口に言ってしまいますと オプションの性質をそのまま合成しますと 証券市場のマーケティング シェアは加算しても0 引いても0という
不思議な性質に出くわすことになります
宣伝広告