広告宣伝
①(有価証券-資産)/T=option
②(有価証券-資産)/2*T=option
③(有価証券-資産)=option*T*T
これらの方程式を説明するのに
必ずしも 微分積分は必要とされていません
もともと方程式の意味 自体が
有価証券と資産の交換によって得られる利益を
2等分しましょうと言っているにすぎないものです
この説明を経済モデルに対応させてみましょう
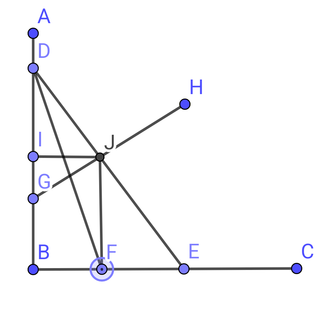
BF 不完全競争占有率
FE 完全競争占有率
③(S-S)=O*T*T
(S-S)=O*BF*FE
DF→DE
限界収入曲線によって市場が2等分されます
需要と供給曲線の交点 J ここで 不完全競争価格が決定され
証券市場内取引ではオプションが
それに相当します
オプション決定後は
市場が解放され
T=1 不完全競争占有率
①(S-S)/T=O
微分積分を関連付けることも可能であると認識いたします
独占価格の一種である オプションは
その性質から
一種の空集合の性格を持っていると
想定されます
☆☆☆☆☆☆☆
占有権→所有権
↓
無権利→無権利
☆☆☆☆☆☆☆
☆☆☆☆☆☆☆
占有権→所有権
↓
無権利→所有権
☆☆☆☆☆☆☆
占有権の状態ではまだ 権利が確定したとは言えず
方程式の中での位置付けが不明という状態です
◐◐◐◐◐◐◐
(S-S)=T*T
↓↑
(S-S)/2=T
◑◑◑◑◑◑◑
Y=T*T
微分積分の関係にあることが分かります
経済モデルが不完全競争状態から完全競争状態に移行した時点で
オプションが確定したことに
その段階で それぞれの方程式に
オプションを参加させるという方法をとります
(S-S)/2*T=O
(S-S)=O*T*T
有価証券の出来高と有価証券の取引に参加している 人数 または有価証券の所有者の数が分かれば そこからその日の銘柄の変動の傾向 または 銘柄の価格を想定することが可能です
有価証券のような資産の80%は富裕層によって所有されていると言われています しかし 個別銘柄ごとによって 70%であったり 60%であったり 流動的である可能性も否定はできません また 有価証券の所有者の数も20%かもしれませんし 30%かもしれませんしたがって 入力項目として 0.2や 0.8に固執する理由はありません
広告宣伝
【このカテゴリーの最新記事】
