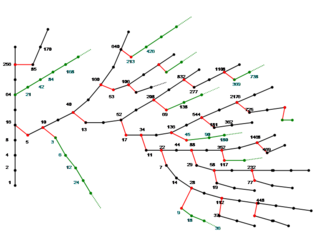
確かに、ここまでの小さな数字ですと、分岐の仕方も単調であり、意外と簡単に解けそうなルールで、それぞれの数字が配置されていそうにも思えてしまいます。
ところが、(前回も少し触れましたが)次の数字「27」で、コラッツの数式は、いきなり、あらぬ方向に進んでしまうのです。
この「27」なのですが、「1」まで分解する為には、実に111回もの計算を必要とするのであります。
しかも、以降の数字の全てが、こんな膨大な計算数を必要としている訳なのでもなく、続く「28、29、30」は再び20回以内の計算に戻ります。「31」は、また3ケタの計算数になりますが、そのあとの「32」から「40」までの数字は、またまた少ない計算数で済み、中には、1ケタの計算で終わってしまう数字(32や40)も混ざっています。
ならば、飛び飛びで巨大な3ケタ計算の数字がポツンポツンと出現するのかと思いきや、必ずしもそうとも言い切れず、「54」と「55」は2つ続けて3ケタ計算ですし、「71」と「73」は、間に数字一つ(72)だけを挟んで、どちらも3ケタ計算です。「107」から「110」までは、3ケタ計算が4つも連続で並びます。
このように、コラッツの数式における数字の配置には、やはり、単純な絶対的パターンが存在していないのであります。少なくとも、現段階では、そのように見えます。
沢山の優れた数学者たちが挑戦しているのにも関わらず、いまだにコラッツ予想が証明されていないと言われるのも、決して伊達ではないのです。
タグ:コラッツ予想