もちろん、数(整数)は無限に存在するのですから、このような事は永遠に実現しません。コンピューターを使って、2の68乗までの数が、コラッツの数式できちんと1になる事が確認されているらしいのですが、それでもなお、コラッツ予想が証明された事にはなっていないのです。
続いて「コラッツ予想を立証する数式」ですが、こちらも、まだ誰も発見してはいないようです。コラッツ予想の解説ページを見ると、ベテランの数学者が過去に作り上げた各種の数式を見かけますが、それらはコラッツの数式の特徴を数式化したものであって、「最後が1になる事」の証明式ではないらしいです。私の無知ぶりが露呈してしまいますので、この辺に関しては、あまり深くは触れません。
本当の証明にはならないかも知れませんが、コラッツの数式における数字どうしの関連性(つながり)をグラフにしてみるという試みもあります。こちらも、コラッツ予想の解説ページを見ると、いろいろな形のグラフを目にする事ができます。
結論は一つのはずなのに、コラッツの数式の計算結果は、さまざまなバリエーションのグラフに直して、書き出せるらしいのです!
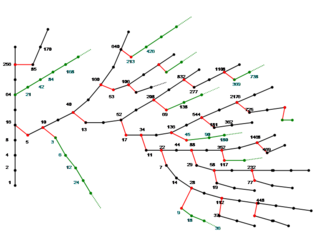
これなんかも、もっともシンプルな形のグラフの一つです。数の分岐の仕方が、まるで生物の進化系統樹のようです。過去に提示されてきたコラッツの数式のグラフは、ほとんどが、こんな形に描かれています。
大自然の摂理(進化系統樹)とソックリだなんて、なんだか、数字という概念も自然の一部である事を、あらためて実感させてくれるのです。
タグ:コラッツ予想






