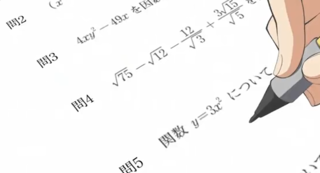航空ロールアウト

関数電卓で確率について試してみる。
確率の中で、今回は「組合わせ」について、関数電卓の機能を使用する。

学校での確率といえば、
「１〜nまでの書かれたカードがあり、それを何枚取り出し、、、」
といった感じであったと思うが、
日常的なことを題材にするのが本ブログの趣旨であるため、ロト６を題材とする。

ロト６とは、軽く説明する。
１〜４３の数字を６個選んでおき、６個とも一致していれば一等で当選である。
賞金は同じ数を選んだ使途の数や、前回当選者の有無（キャリーオーバー）にもよるが、１億円といったところ。

ｎ個のなかからr個取り出すときの、組合わせの式は以下である。高校の数学である。

ｎＣｒ

ロト6の場合、43個の数字から6個を取り出すのであるから「43Ｃ6」である。

関数電卓で作業する。
シャープEL-509Tの場合、以下のキーを打つと、結果表示される。

［４］［３］［2ndF］［nCr］［６］［＝］

結果は「6,096,454」（600万）である。
つまり、1等は、600万分の1である。

ちなみに、普通の電卓で行うのであれば、以下の計算で同じ結果となる。
43 × 42 × 41 × 40 × 39 × 38 ÷6 ÷ 5 ÷ 4 ÷ 3 ÷ 2 ÷ 1 = 6,096,454

さて、
ロト6は週2回行われ、１年は52週である。
計算すると、43Ｃ6÷2÷52≒58,000
6万年毎回購入し続ければ1回は当たるような確率である。


確率ではそうなるが、当選することが決まったわけではない。確実に当選するには6,096,454口を購入すればよい。


以上

ＰＳ　
おまけ、ロト6を用いた組み合わせの記事
関数電卓：組み合わせ　その２
https://fanblogs.jp/kokurollout/archive/33/0