���d��ŎZ�o���Ă݂�B
�Ȃ��A���K����AI�iCopilotGPT�j�ŏo�肵�Ă�������B
���K���F
����G����w�������Ƃ���A�w�����1�N�ԂŊG��̉��l��10%�オ��A����1�N�Ԃł���ɉ��l��15%�オ��A���̎���1�N�Ԃł���ɉ��l��20%�オ��܂����B����3�N�Ԃɂ����āA�G��̉��l�͔N���ςłǂꂭ�炢�㏸�����ł��傤���H
�F
1�N�ڂ̏㏸����10%�Ȃ̂ŁA���l�͌��̉��l��1.10�{�ɂȂ�܂��B
2�N�ڂ̏㏸����15%�Ȃ̂ŁA���l��1.10�{��1.15�{�ɂȂ�܂��B
3�N�ڂ̏㏸����20%�Ȃ̂ŁA���l��1.10 × 1.15 × 1.20 = 1.518�{�ɂȂ�܂��B
���������āA3�N�Ԃ̑��敽�ρi�N���ς̐������j�͎��̂悤�Ɍv�Z�ł��܂��F
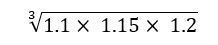
�v�Z����ƁA���敽�ς͖�1.149�ł��B���������āA�G��̉��l�͔N���ςŖ�14.9%�㏸���܂���
���d��ł̑���F
���d��ł͎��̃{�^������ƂȂ�B
�i���d��̓V���[�v�Ђ�EL-509T���g�p���Ă��邪�A���А��ł������ς��͂Ȃ��ł��j
�m3�n�mx��n�i�m2ndF�n�myx�n�j�m0�n�m.�n�m1�n�m�n�m1�n�m.�n�m1�n�m5�n�m�n�m1�n�m.�n�m2�n�m���n

���[�g�̌v�Z����ɂ���ꍇ�͏㏸���݂̂��ɎZ�o�i�@�j���A�Z�o���ʂɑ����[�g���s���i�A�j�悤�ɂ���B�O��̌��ʂ́mANS�n�{�^���Ŏg�p�ł��邱�Ƃ𗘗p���܂��B
�@�m0�n�m.�n�m1�n�m�n�m1�n�m.�n�m1�n�m5�n�m�n�m1�n�m.�n�m2�n�m���n
�A�m3�n�mx��n�i�m2ndF�n�myx�n�j�mANS�n�i�mALPHA�n�m���n�j�m���n


���[�g�ł͂Ȃ��A�ׂ���ŋ��߂Ă��悢
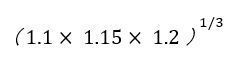
�A'�mANS�n�i�mALPHA�n�m���n�j�myx�n�m1�n�m÷�n�m3�n�m���n�܂���
�A'�f�mANS�n�i�mALPHA�n�m���n�j�myx�n�m1�n�ma/b�n�m3�n�m���n

�G�N�Z���Ŋ��ρi���敽�ρj
�G�N�Z���ł́uGEOMEAN�v�Ƃ������ŋ��߂邱�Ƃ��ł���B
�ȏ�
�^�O�F���d��
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
-
no image
-
no image
-
no image
-
no image
-
no image
-
no image
-
no image