パプリカ2020の部屋

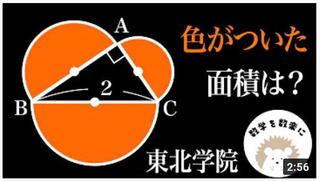
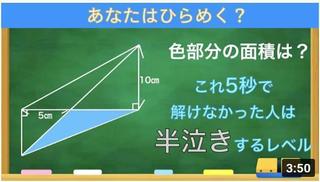
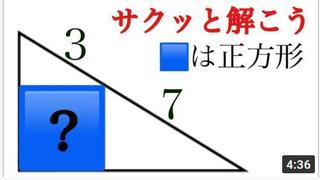
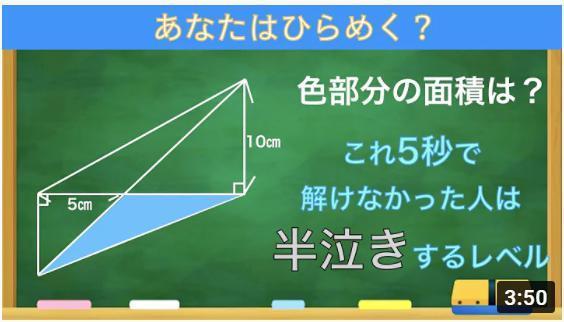
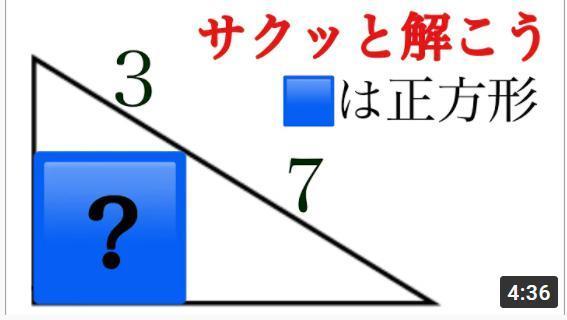
Ｑ：3つの半円の面積の和

Ａ：頂点Ａの対辺の長さをa　とする。
同様に頂点Ｂの対辺の長さをb、
頂点Ｃの対辺の長さをc　とする。

直径aで作る半円の面積をＳaとする。
同様に直径bで作る半円の面積をＳb、
直径ｃで作る半円の面積をＳc　とする。

3つの半円の和をＳとすると、
Ｓ＝Ｓa＋Ｓb＋Ｓc
　＝(1/2)*π*(a/2)^2＋(1/2)*π*(b/2)^2＋(1/2)*π*(c/2)^2
　＝(π/8）*(a^2＋b^2＋c^2)　・・・�@

ここで�凾`ＢＣは∠Ａが∠Ｒの直角三角形なので
三平方の定理より
　a^2＝b^2＋c^2
またa＝2　から　a^2＝4＝b^2＋c^2
よって�@式は
　(π/8)*(4＋4)＝π

したがって与えられた3つの半円の面積の和は　π