厳選　中学数学のおすすめ参考書

この広告は30日以上更新がないブログに表示されております。
新規記事の投稿を行うことで、非表示にすることが可能です。

パスカルの三角形をご紹介します。見たことはあるでしょうか？
ある規則にしたがって出来ています。

───────────────────────────────────────────────
※パスカルの三角形の作り方

図のように、
上の段にある隣接する二つの数字の和を
どんどん計算して、
下へ下へと書き足して出来ています。


　何度か適当に一つ数字を選んで、確認してみてください。



────────────────────────────────────────────────
パスカルの三角形には、びっくりするほどたくさんの不思議が潜んでいます。


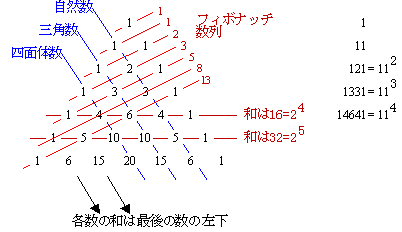
右図を見てください。
まずは斜めの並びに注目

青のラインに
自然数1、2、3、4、5、6・・・
三角数1、3、6、10、15・・・
四面体数1、4、10、20・・・

角度を変えると、
フィボナッチ数列まで現れています。
（※三角数やフィボナッチ数については、
別記事で。クリックで飛びます）

また横の並びに注目すると、
2段目の和　1+1＝2　→2の１乗
3段目の和　1+2+1＝4　→2の2乗
4段目の和　1+3+3+1＝8　→2の3乗
5段目、6段目は図の通りです。

さらに、横の数字の並びは、11,121,1331,14641となっていますが、
これは、図の右に書いてあるように11の累乗になっています。
─────────────────────────────────────────────────


中学3年生〜高校生の内容になりますが、
左図も有名です。
展開したあとの係数になっています。
暗記の必要がなくなるので、知っておくと便利。




インターネットを活用した次世代型完全個別指導塾【ネット松陰塾】

─────────────────────────────────────────────────
最後におまけ。
パスカルの三角形を2の倍数、3の倍数、5の倍数で塗りつぶしてみました。
綺麗な模様が浮かび上がります。不思議すぎです。

ものを数えるという事からはじまり考案され、
これにゼロという不思議な数を加えた数字の世界。
時に魔法とでも思えるような、とても魅力的でゾクゾクするような規則性が潜んでいます。

以下、例を挙げると

1だけを使った掛け算で1〜9までの全ての数が現れる
9801分の1　

　1/9801= 0.
　　00 01 02 03 04 05 06 07 08 09
　　10 11 12 13 14 15 16 17 18 19
　　20 21 22 23 24 25 26 27 28 29
　　30 31 32 33 34 35 36 37 38 39
　　40 41 42 43 44 45 46 47 48 49
　　50 51 52 53 54 55 56 57 58 59
　　60 61 62 63 64 65 66 67 68 69
　　70 71 72 73 74 75 76 77 78 79
　　80 81 82 83 84 85 86 87 88 89
　　90 91 92 93 94 95 96 97 99 　　　
　※最後は100が繰り上がって98だけ消える
　※9801は99の2乗です

循環する数？不思議な数　142857

　　142857 × 1 = 142857
　　142857 × 2 = 285714　　142857142857
　　142857 × 3 = 428571　　142857142857
　　142857 × 4 = 571428　　142857142857
　　142857 × 5 = 714285　　142857142857
　　142857 × 6 = 857142　　142857142857

　　142857 × 7 = 999999
　　14 + 28 + 57 = 99
　　142 + 857 = 999

この他にもフィボナッチ数列やパスカルの三角形といった不思議すぎる数字の魅力はまだまだあります。
そちらは別記事にて紹介しています

タイトルを見たら何を言ってるんだと思うかもしれませんが そんな夢のような教科あります。 数学です。 数学の好きなところを聞かれると、答えが一つだから、と返す人が多いと思います。 確かに数学は答えが一つになります。 しかし、答えにたどり着くために通るルートが実はたくさんあって 単純な計算問題でも、計算の順番を入れ替えたり、変形したり、工夫の余地があります。 このルートというのが人によってバラバラになることのある部分。 ここで、一番簡単な方法を考え、思いつき、 人より楽をして解いた人が褒められるのが数学というわけです。 水を汲んで来いといわれてホースを引っ張ってくるような、ずる賢いひねくれもの向きの、 考えるほどに楽しくなる教科なんです。 例えばこんな問題どう解きますか？　※暗算推奨 9+99+999 16×25 19×45 29×31 99×999 これをバカ正直に筆算しても、しんどいし、めんどくさいし、なにより正解しても楽しくない。 ちょっと工夫をしてなんとか楽を出来ないか、考える事。 きっと何かが隠されていて、うまく解く方法があるはずだ、といつも考えてる人はデキるやつ。 中学三年間を終える頃には、このちょっとした取り組み方の違いで、雲泥の差がついています。 以下に、上の問題の考え方の一例を挙げておきます。 9+99+999=（10-1）+（100-1）+（1000-1）=10+100+1000-3=1110-3＝1107 16×25＝（4×4）×25＝4×（4×25）＝4×100＝400 19×45＝20×45-1×45＝900-45＝855　 29×31＝（30-1）×（30+1）＝900-1＝899　※中学3年で展開公式を習ったあとなら 　29×31＝30×31-1×31＝930-31＝899 99×999＝100×999-1×999＝99900-999＝99900-1000+1＝98901 どうでしたか？ もっとうまい方法もあるかもしれません。