厳選　中学数学のおすすめ参考書

フィボナッチという言葉は、イタリアの数学者レオナルドの通称が由来。
ボナッチさんの息子という意味のfilio BonacijがなまってFibonacciフィボナッチと呼ぶようになった、と言われています。

フィボナッチ数列は、ボナッチさんの息子であるレオナルドの記した「算盤の書」の中の有名な「兎の問題」に出てきます。
以下に兎の問題を紹介します。

条件
a.1対の子ウサギがいる。
b.子ウサギは1ヶ月たつと親ウサギになる。
c.親ウサギは1ヶ月たつと子ウサギを産む。
問
この条件で、どのウサギも死なないものとした時、1年後には何対のウサギがいるか。

解法

子ウサギ○
親ウサギ●

0ヶ月後（スタート）
○　1
1ヶ月後
●　1
2ヵ月後
○●　1+1＝2
3ヵ月後
○●●　1+2＝3
4ヵ月後
○○●●●　2+3＝5
5ヵ月後
○○○●●●●●　3+5＝8
6ヵ月後
○○○○○●●●●●●●●　5+8＝13
7ヵ月後
○○○○○○○○●●●●●●●●●●●●●　8+13＝21
8ヵ月後
○○○○○○○○○○○○○●●●●●●●●●●●●●●●●●●●●●　13+21＝34
9ヵ月後
○○○○○○○○○○○○○○○○○○○○○●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●　21+34＝55
10ヵ月後
ここからは数が多くなるため省略しますが、少し補足説明を入れます。
　9ヶ月後の時点の親34対から子が34対産まれ、
　親子合わせて55対居たウサギは全て親になるので、
子34+親55＝89　と、なる。
11ヵ月後
同様に、55+89＝144
12ヵ月後（1年後）
同様に、89+144＝233

答
233対

こうして生まれたのがフィボナッチ数列です。
1　1　2　3　5　8　13　21　34　55　89　144　233　・・・

インターネット自宅学習システム「ｅ点ネット塾」


この数列の続きは、もう予想できていると思いますが、
前2項の和の377（＝144+233）
次が、610（＝233+377）　と、続きます。

この数列は、数学の世界だけではなく、芸術の世界や自然界と深く関わる
なんとも不思議な数列なのです。
例を挙げると

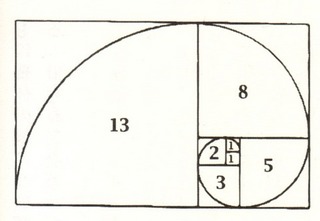
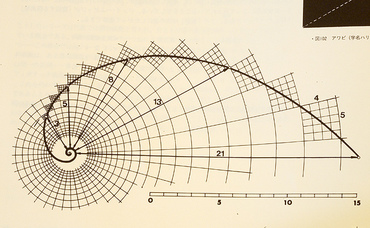
貝の渦巻きにフィボナッチ数が現れたり

1　1　2　3　5　8　13　21　34　55　89　144　233　・・・
と続くフィボナッチ数を、
隣同士の数で割り算すると

1÷1=1
2÷1=2
3÷2=1.5
5÷3=1.66・・・
8÷5=1.6
13÷8=1.625
21÷13=1.615･･･
34÷21=1.619･･･

そこに表れた数字は、
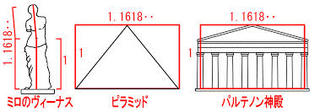
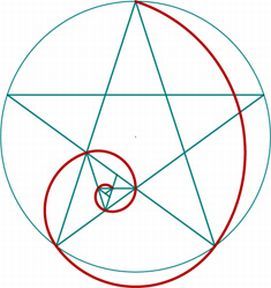
"パルテノン神殿"や"モナリザ"、またピタゴラス教団のシンボルである"五芒星"に現れる、
最も美しい比率と呼ばれる1:1.618の黄金比
身近なところで言うと、名刺や漫画なども短辺と長辺の比が黄金比になっています


インターネット家庭教師Netty

少し話はそれますが
ドレミの12音階もピタゴラス音階と呼ばれるようにピタゴラスによって作られていますし
レオナルドダヴィンチは絵を描くなら数学の勉強をしろと言ったし
われらが葛飾北斎も定規とコンパスで構図を決めていました



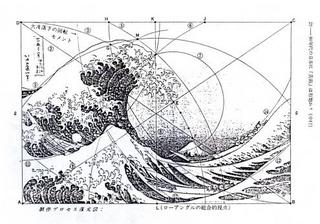
数字と自然や芸術は切っても切れない関係と言えるかもしれません