新規記事の投稿を行うことで、非表示にすることが可能です。
2011年10月25日
フィボナッチ数列の紹介
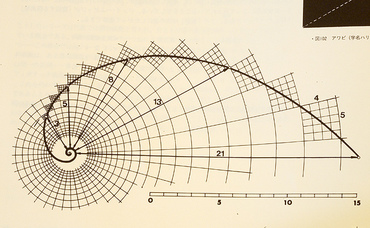
フィボナッチという言葉は、イタリアの数学者レオナルドの通称が由来。
ボナッチさんの息子という意味のfilio BonacijがなまってFibonacciフィボナッチと呼ぶようになった、と言われています。
フィボナッチ数列は、ボナッチさんの息子であるレオナルドの記した「算盤の書」の中の有名な「兎の問題」に出てきます。
以下に兎の問題を紹介します。
条件
a.1対の子ウサギがいる。
b.子ウサギは1ヶ月たつと親ウサギになる。
c.親ウサギは1ヶ月たつと子ウサギを産む。
問
この条件で、どのウサギも死なないものとした時、1年後には何対のウサギがいるか。
解法
子ウサギ○
親ウサギ●
0ヶ月後(スタート)
○ 1
1ヶ月後
● 1
2ヵ月後
○● 1+1=2
3ヵ月後
○●● 1+2=3
4ヵ月後
○○●●● 2+3=5
5ヵ月後
○○○●●●●● 3+5=8
6ヵ月後
○○○○○●●●●●●●● 5+8=13
7ヵ月後
○○○○○○○○●●●●●●●●●●●●● 8+13=21
8ヵ月後
○○○○○○○○○○○○○●●●●●●●●●●●●●●●●●●●●● 13+21=34
9ヵ月後
○○○○○○○○○○○○○○○○○○○○○●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●● 21+34=55
10ヵ月後
ここからは数が多くなるため省略しますが、少し補足説明を入れます。
9ヶ月後の時点の親34対から子が34対産まれ、
親子合わせて55対居たウサギは全て親になるので、
子34+親55=89 と、なる。
11ヵ月後
同様に、55+89=144
12ヵ月後(1年後)
同様に、89+144=233
答
233対
こうして生まれたのがフィボナッチ数列です。
1 1 2 3 5 8 13 21 34 55 89 144 233 ・・・
インターネット自宅学習システム「e点ネット塾」
この数列の続きは、もう予想できていると思いますが、
前2項の和の377(=144+233)
次が、610(=233+377) と、続きます。
この数列は、数学の世界だけではなく、芸術の世界や自然界と深く関わる
なんとも不思議な数列なのです。
例を挙げると
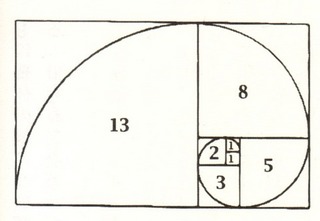
貝の渦巻きにフィボナッチ数が現れたり
1 1 2 3 5 8 13 21 34 55 89 144 233 ・・・
と続くフィボナッチ数を、
隣同士の数で割り算すると
1÷1=1
2÷1=2
3÷2=1.5
5÷3=1.66・・・
8÷5=1.6
13÷8=1.625
21÷13=1.615・・・
34÷21=1.619・・・
そこに表れた数字は、
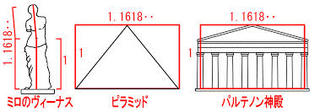
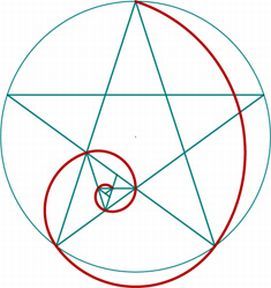
"パルテノン神殿"や"モナリザ"、またピタゴラス教団のシンボルである"五芒星"に現れる、
最も美しい比率と呼ばれる1:1.618の黄金比
身近なところで言うと、名刺や漫画なども短辺と長辺の比が黄金比になっています
インターネット家庭教師Netty
少し話はそれますが
ドレミの12音階もピタゴラス音階と呼ばれるようにピタゴラスによって作られていますし
レオナルドダヴィンチは絵を描くなら数学の勉強をしろと言ったし
われらが葛飾北斎も定規とコンパスで構図を決めていました
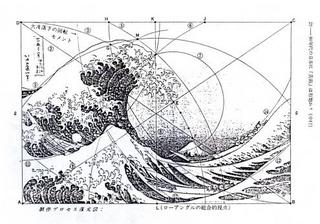
数字と自然や芸術は切っても切れない関係と言えるかもしれません
2011年10月22日
心構えの違い

たいして努力していないように見えるのに、やたらとデキる人。居ますよね。
教えがいのないほど良く出来る子は、いったい何が違うのだろうと考えるのですが、
一番大きなポイントは、 わからない事を放置しない だと思います。
毎日何時間も勉強している子は別として、
同じような勉強量でもなぜか差が出ていきます。
同じ量(時間)の努力をしているのですから、そういった心構えの差が出るのでしょう。
才能や頭の出来が違うといった反論もありそうですが、
はっきり言って中学生の勉強において、才能なんてのは微々たる影響しかありません。
疑問を持ったらわからないまま放置せず、何かに気づきかけたらそれを形にするまで考える。
この過程において、諦めの早さが覚えの悪さに、粘り強さがセンスに変わっていきます。
自分の限界をこの程度、と決めつけていては、
わからない事があっても、まあこんなもんだろうと、すぐに諦める癖が付き、
ますます自信を失って、勉強できないルート行き。これは勿体無い。
あとで、ではなく「今」なんとかしよう。という気持ちを持つだけでいい。
わかるまで納得しない諦めない。
その心構えからくる積み重ねが、デキる人への最短ルートです。
長時間頑張れって事ではなく、諦めかけたときに”あと5分”集中して踏ん張ってみる。
その程度でいいんです。
極端な話、授業中の50分で片をつけてしまえば、テスト勉強なんか必要ありません。
授業中に全てわかってやろうと挑戦してみてください。
為せば成る。
どうせ50分机に拘束されるんだから、ここぞとばかりに集中してやってしまいましょう。
そして、テスト期間中は遊びましょう。
わからない事を放置するのは罪。
テスト期間中に何時間も勉強する罰や、
テストの返却の時間に憂鬱になる罰を、
知らぬ間に受けているのです。
2011年10月19日
三角数の話

三角数をとりあえず、10個並べてみます
1 3 6 10 15 21 28 36 45 55 …
もちろん適当に並べたわけではなく、ある法則によって決まった数。
この時点で何かに気づいた人はかなり鋭い。
では、どのような数であるかを紹介します。
三角数は、正三角形の形に点を並べたときに、そこに並ぶ点の総数 です。
今はもう馴染みがないかもしれませんが、米俵の積み方と同じ。

1 1+2=3 3+3=6 6+4=10
1〜4番目の三角数は図の通り、1 3 6 10 です。
続けると、5番目以降が、15 21 28 ・・・となる事を確認してください。
ここで、色の付いた部分に注目すると、足す数が一つずつ増えている事がわかります。
1番目の三角数 1=1
2番目の三角数 3=1+2 1〜2の自然数を足したもの
3番目の三角数 6=1+2+3 1〜3の自然数を足したもの
4番目の三角数 10=1+2+3+4 1〜4の自然数を足したもの
5番目の三角数 15=1+2+3+4+5 1〜5の自然数を足したもの
※下線部は、一つ前の三角数 色付き部分が、増える数 です。
面白い数でしょ?専用の名前(三角数)が付いているのも納得です。
──────────────────────────────────────────────────
・100番目の三角数の求め方
100番目の三角数 ?=1+2+3+・・・+98+99+100 1〜100の自然数を足したもの
これを求めるために単純に足していくとすごく時間がかかるので
天才少年ガウスの計算方法に頼りましょう。
<順と逆に並べ、1と100、2と99、3と98という風に上下でセットを作ります>
1 + 2 + 3 + 4+ ・・・ +98+99+100 = 100番目の三角数
100+99+98+97+ ・・・ +3 + 2 + 1 = 100番目の三角数
<上下を足していきます>
101+101+101+101+ ・・・ +101+101+101 = 101×100
(※101のセットが100個出来ました。)
となり、101×100=10100
10100は、100番目の三角数を二回足した数なので、
100番目の三角数=10100÷2=5050 と、なります。
ちなみに、考え方を拡張すると、n番目の三角数を求められます。
意欲のある人は、上の考え方を参考にして、
n番目の三角数をnを使った式で表してみてください。
定期テストや受験でもよく出てくるパターンの問題です。
ヒント 1+2+3+ ・・・ +n=n番目の三角数